10.5. Определение количественной оценки ошибки выборки и построение доверительных интервалов выборочных характеристик

В процессе проведения выборочного наблюдения, как и вообще при анализе данных любого обследования, статистика выделяет два вида ошибок: регистрации и репрезентативности.

Ошибки регистрации – ошибки, связанные с процессом сбора данных.

Ошибки репрезентативности – ошибки, связанные с тем, оценки параметров всей совокупности единиц находятся на основе частичных, неполных данных.

Ошибка выборочного наблюдения (репрезентативности) - это разность между величиной параметра в генеральной совокупности и его величиной, вычисленной по результатам выборочного наблюдения.

Ошибки репрезентативности в выборочной совокупности, сформированной случайным образом, является случайной величиной и поддается оценке инструментами теории вероятностей.

Для измерения ошибки выборки определяется ее средняя ошибка по формуле (10.12) для повторного отбора и по формуле (10.22) – для бесповторного:

= ; (10.12) = . (10.22)

Из формул (10.12) и (10.22) видно, что средняя ошибка меньше у бес­повторной выборки, что и обусловливает ее более широкое применение.

Учитывая, что на основе выборочного обследования нельзя точно оценить обобщающую характеристику ГС, необходимо найти пределы, в которых она находится. Зная среднюю ошибку выборки, с определенной вероятностью можно оценить отклонение выборочной средней от генеральной и установить пределы, в которых находится изучаемый параметр (в данном случае среднее значение) в генеральной совокупности. Максимальную величину отклонения среднего значения признака по выборке от среднего значения признака по генеральной совокупности с определенной степенью вероятности называют предельной ошибкой выборочной оценки, а соответствующую вероятность – доверительной вероятностью.

Предельная ошибка средней величины рассчитывается по формуле:

= t , (10.32)

где t – коэффициент доверия, зависящий от доверительной вероятности, с которой определяется предельная ошибка выборки.

Вероятность появления определенной ошибки выборки находят с помощью теорем теории вероятностей. Согласно теореме Чебышёва, при достаточно большом объеме выборки и ограниченной дисперсии генеральной ГС вероятность того, что разность между выборочной средней и генеральной средней будет сколь угодно мала, близка к единице:

при . (10.4)

А. М. Ляпунов доказал, что независимо от характера распределения генеральной ГС при увеличении объема выборки распределение вероятностей появления того или иного значения выборочной средней приближается к нормальному распределению (центральная предельная теорема). Следовательно, вероятность отклонения выборочной средней от генеральной средней, т.е. вероятность появления заданной предельной ошибки, также подчиняется указанному закону и может быть найдена как функция от t с помощью интеграла вероятностей Лапласа:

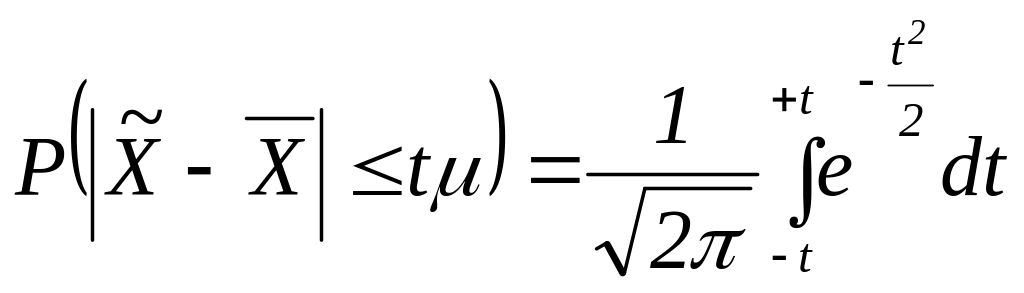, (10.5)

где – нормированное отклонение выборочной средней от генеральной средней.

Значения t для заданных Р находятся по таблицам значений функции Лапласа. Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной средней.

Вероятность Р, которая принимается при расчете выборочной характеристики, называется доверительной. Чаще всего принимают вероятность P = 0,950, которая означает, что только в 5 случаях из 100 ошибка может выйти за установленные границы. В статистике существуют наиболее распространенные уровни вероятностей, например: 0,954; 0,997 и др. Это означает, что, соответственно, в 6 случаях из 1000 и в 3 случаях из 1000 ошибка выборки может превысить пределы, определенные выборочным наблюдением.

После расчета предельной ошибки находят доверительный интервал обобщающей характеристики ГС совокупности по формуле (10.6) – для среднего значения, и по формуле (10.7) – для доли единиц, обладающих каким-либо значением признака:

или ( – ) ( + ) (10.6)

или ( – ) d ( + ) (10.7)

Следовательно, при выборочном наблюдении определяется не одно, точное значение обобщающей характеристики ГС, а лишь ее доверительный интервал с заданным уровнем вероятно­сти. И это серьезный недостаток выборочного метода статистики.

Пример. Методом случайного бесповторного отбора были отобраны 150 государственных служащих региона, что составляет 3% от общей численности госслужащих региона. В результате было установлено, что средняя заработная плата в январе 2001 года составила 6000 руб. С вероятностью 0,954 определить пределы, в которых находится средняя заработная плата всех государственных служащих региона, если из предыдущих исследований известно, что среднее квадратическое отклонение составляет 450 руб.

Решение: Метод отбора предполагает использование в расчетах поправки на бесповторность. Имеем: n = 150 (чел.) – количество государственных служащих (единиц выборочной совокупности); = 6000 (руб.) – средняя заработная плата, т.е. исследуемый параметр выборочной совокупности; = 450 (руб.) – среднее квадратическое отклонение; N – общая численность государственных служащих региона; P(t) = 0,954 – доверительная вероятность появления ошибки выборки определенного размера.

1 шаг. Определение численности генеральной совокупности:

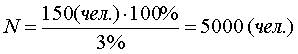2 шаг. Определение средней ошибки выборочной средней для бесповторного отбора:

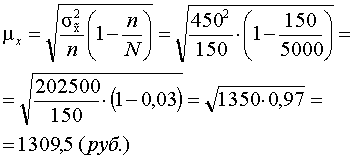То есть, отклонение средней заработной платы всех госслужащих региона (генеральной совокупности) от средней заработной платы группы обследованных госслужащих (выборочной совокупности) в среднем составило 1309,5 рублей.

2 шаг. Определение предельной ошибки выборочной средней: по таблицам значений функции Лапласа при Р = 0,954 находим значение t = 2

Тогда, 3 шаг. Расчет границ доверительного интервала, в пределах которого будет колебаться значение средней в генеральной совокупности:

То есть, с вероятностью 0,954 можно утверждать, что средняя заработная плата всех госслужащих региона не меньше, чем 3381 рублей, но не больше, чем 8619 рублей.

Принцип транспонирования (переноса, распространения) выводов о выборке на генеральную совокупность, принятый для средних величин, сохраняется и при определении показателей доли:

1. Средняя ошибка выборки ( )для доли (w) единиц, обладающих изучаемым признаком, при повторном отборе:

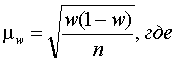w – удельный вес единиц, обладающих изучаемым признаком; – дисперсия для показателя доли; n – численность единиц выборочной совокупности.

2. Средняя ошибка выборки ( )для доли (w) единиц, при бесповторном отборе:

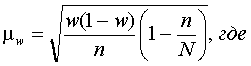N – численность единиц генеральной совокупности.

3. Предельная ошибка выборочной доли ( ): Тогда, удельный вес единиц, обладающих изучаемым признаком, в генеральной совокупности будет находиться в пределах:

Пример. Для анализа условий жизни студентов проведено выборочное обследование методом случайного бесповторного отбора. Из 100 обследованных студентов института 20 человек снимали квартиры. Требуется с вероятностью 0,997 определить долю студентов всего института (700 чел.), снимающих квартиру.

Решение: В обозначениях, введенных выше, имеем:

n = 100 (чел.) – количество обследованных студентов (единиц выборочной совокупности);

N = 700 (чел.) – число студентов всего института;

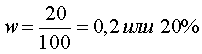– доля студентов, снимающих квартиру в выборочной совокупности;

P(t) = 0,997 – вероятность появления ошибки определенного размера.

1 шаг: Определение средней ошибки выборочной доли для бесповторного отбора:

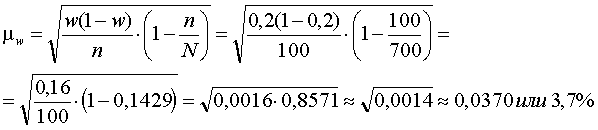То есть, отклонение удельный вес студентов института, снимающих квартиру в общей численности студентов института от доли, полученной в результате выборки, составит 3,7%.

2 шаг: Определение предельной ошибки выборочной доли. Согласно таблице нормального закона распределения значение t при Р = 0,997 равно 3. Отсюда:

Тогда, удельный вес студентов, снимающих квартиру, среди всех студентов института будет находиться в пределах:

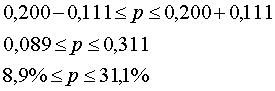То есть, с вероятностью 0,997 можно утверждать, что удельный вес студентов, снимающих квартиру, в общей численности студентов будет не меньше 8,9%, но не больше чем 31,1%.