1. Размах вариации

Определение. Размахом вариации называется разница между наибольшим и наименьшим результатами выборки, обозначается R и определяется

R=X_max - X_min .

Информативность этого показателя невелика, хотя при малых объёмах вы­борки по размаху легко оценить разницу между лучшим и худшим результатами спортсменов.

2. Дисперсия

Определение. Дисперсией называется средний квадрат отклонения значений признака от среднего арифметического.

Для не сгруппированных данных дисперсия определяется по формуле

² = ,

где Х_i – значение признака, - среднее арифметическое.

Для данных, сгруппированных в интервалы, дисперсия определяется по формуле

,

где х_i – среднее значение i интервала группировки, n_i – частоты интервалов.

Для упрощения расчётов и во избежание погрешностей вычисления при округ­лении результатов (особенно при увеличении объёма выборки) используются также другие формулы для определения дисперсии. Если среднее арифметическое уже вычислено, то для не сгруппированных данных используется следующая фор­мула:

² = ,

для сгруппированных данных:

.

Эти формулы получаются из предыдущих раскрытием квадрата разности под знаком суммы.

В тех случаях, когда среднее арифметическое и дисперсия вычисляются од­новременно, используются формулы:

для не сгруппированных данных:

² = ,

для сгруппированных данных:

.

3. Среднее квадратическое (стандартное) отклонение

Определение. Среднее квадратическое (стандартное) отклонение характе­ризует степень отклонения результатов от среднего значения в абсолютных единицах, т. к. в отличие от дисперсии имеет те же единицы измерения, что и результаты измерения. Иначе говоря, стандартное отклонение показывает плотность распределения результатов в группе около среднего значения, или однородность группы.

Для не сгруппированных данных стандартное отклонение можно определить по формулам

 = ,

 = или  = .

Для данных, сгруппированных в интервалы, стандартное отклонение определяется по формулам:

,

или .

4. Ошибка средней арифметической (ошибка средней)

Ошибка средней арифметической характеризует колеблемость средней и вычисляется по формуле:

.

Как видно из формулы, с увеличением объёма выборки ошибка средней уменьшается пропорционально корню квадратному из объёма выборки.

5. Коэффициент вариации

Коэффициент вариации определяется как отношение среднего квадратического отклонения к среднему арифметическому, выраженное в процентах:

.

Считается, что если коэффициент вариации не превышает 10 %, то выборку можно считать однородной, то есть полученной из одной генеральной совокупности.

Характеристики формы распределения

Кривая эмпирического распределения не всегда идеально колоколообразна (нормальна) и симметрична. Отсюда и следует важность вычисления коэффициентов асимметрии и эксцесса для эмпирических рядов распределения, т. к. они характеризуют скошенность и крутость данного ряда по сравнению с нормальным.

Для многих распределений характерен сдвиг кривой влево или вправо. В связи с этим различают левостороннюю (положительную) и правостороннюю (отрицательную) асимметрию. Она зависит от знака формулы для определения коэффициента асимметрии (нормированного центрального момента третьего порядка), который служит характеристикой скошенности или асимметрии распределения, определяемой по формулам:

• для не сгруппированных данных:

,

где - центральный момент третьего порядка, - среднее квадратическое отклонение, х_i – значение признака, - среднее арифметическое, n – объём выборки;

• для данных, сгруппированных в интервалы:

,

где n_i – частоты интервалов группировки, x_i – срединное значение i интервала группировки, k – число интервалов.

При этом, если знак этого выражения отрицательный (-), то асимметрия правосторонняя, или отрицательная (рис. 10.8), если же знак положительный (+), то асимметрия левосторонняя, или положительная (рис. 10.9).

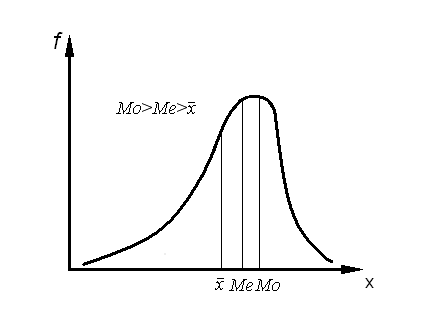
Рис.10.8. Правосторонняя (отрицательная) асимметрия

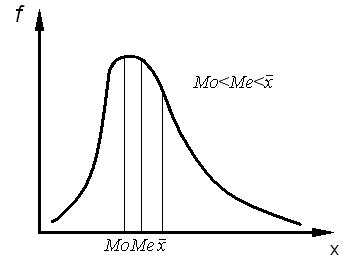
Рис. 10.9. Левосторонняя (положительная) асимметрия

Наиболее простой показатель асимметрии – это мера скошенности:

.

В основу её положено отклонение средней арифметической от моды, а по знаку выражения определяется левосторонняя (положительная) или правосторонняя (отрицательная асимметрия).

Кроме асимметричности кривые распределения имеют характеристики плосковершинности и островершинности. Их характеристикой служит величина эксцесса (нормированного центрального момента четвёртого порядка, см. учебник), которая рассчитывается по формулам:

• для не сгруппированных данных:

,

где х_i - значение признака;

• для сгруппированных данных

,

где n_i - частоты интервалов группировки;

х _i - срединное значение интервала группировки;

σ - среднеквадратическое отклонение.

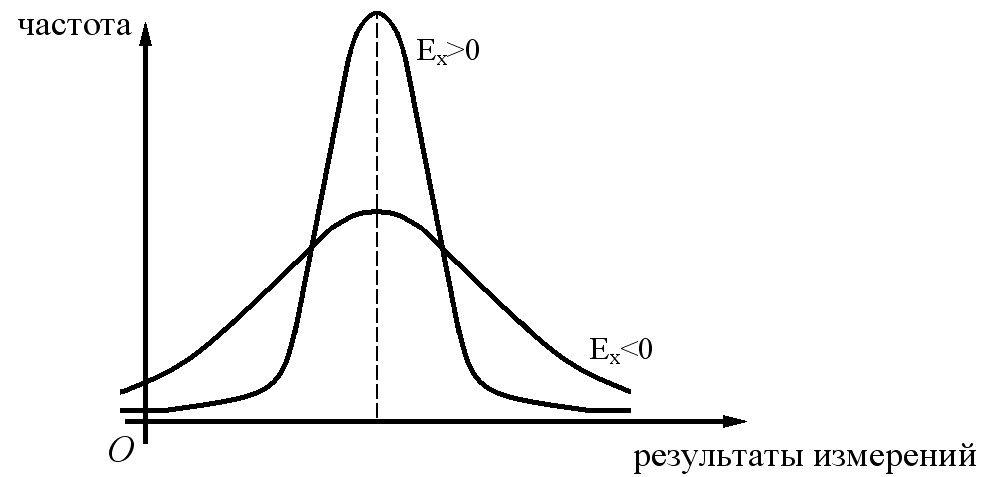
Рис. 10.10. Островершинная и плосковершинная кривые распределения

Если знак эксцесса отрицательный (-), то имеется тенденция к плосковершинности (рис.10.10).

Если же знак положительный (+), то имеется тенденция к островершинности (рис. 10.10).