Характеристики положения
1. Среднее арифметическое значение
Среднее арифметическое значение – одна из основных характеристик выборки.
Она, как и другие числовые характеристики выборки, может вычисляться как по необработанным первичным данным, так и по результатам группировки этих данных.
Точность вычисления по необработанным данным выше, но процесс вычисления оказывается трудоёмким при большом объёме выборки.
Для не сгруппированных данных среднее арифметическое определяется по формуле:
,
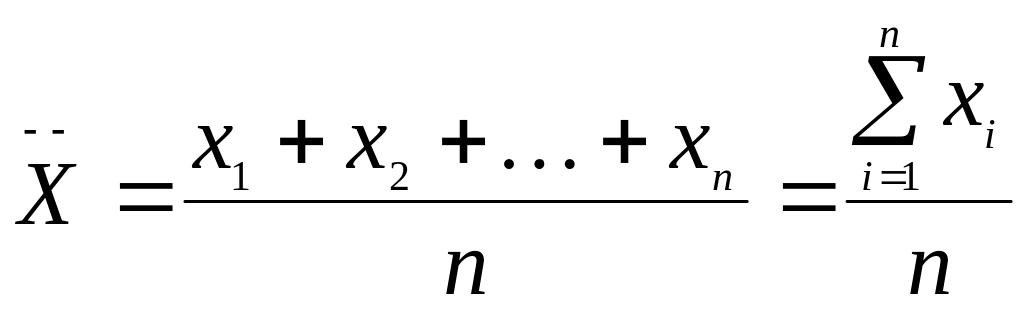где n- объем выборки, х1, х2, ... хn - результаты измерений.
Для сгруппированных данных:
,
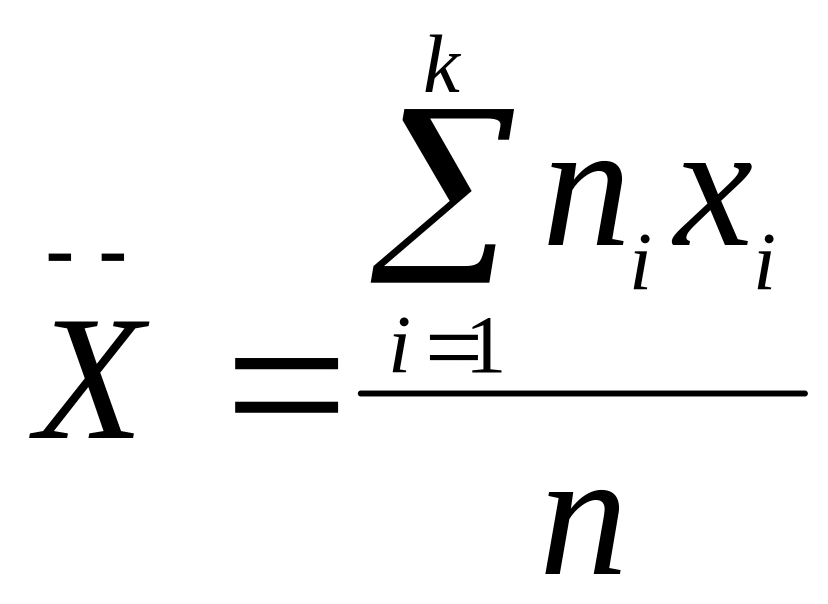где n- объем выборки, k – число интервалов группировки, ni – частоты интервалов, xi – срединные значения интервалов.
2. Мода
Определение 1. Мода - наиболее часто встречающаяся величина в данных выборки. Обозначается Мо и определяется по формуле:
,
где
-
нижняя граница модального интервала,
- ширина интервала группировки,
-
частота модального интервала,
-
частота интервала, предшествующего
модальному,
-
частота интервала, последующего за
модальным.
Определение 2. Модой Мо дискретной случайной величины называется наиболее вероятное её значение.
Геометрически моду можно интерпретировать как абсциссу точки максимума кривой распределения. Бывают двухмодальные и многомодальные распределения. Встречаются распределения, которые имеют минимум, но не имеют максимума. Такие распределения называются антимодальными.
Определение. Модальным интервалом называется интервал группировки с наибольшей частотой.
3. Медиана
Определение. Медиана - результат измерения, который находится в середине ранжированного ряда, иначе говоря, медианой называется значение признака Х, когда одна половина значений экспериментальных данных меньше её, а вторая половина – больше, обозначается Ме.
Когда объем выборки n - четное число, т. е. результатов измерений четное количество, то для определения медианы рассчитывается среднее значение двух показателей выборки, находящихся в середине ранжированного ряда.
Для данных, сгруппированных в интервалы, медиану определяют по формуле:
,
где
-
нижняя граница медианного интервала;
ширина интервала группировки, 0,5n
– половина объёма выборки,
-
частота медианного интервала,
-
накопленная частота интервала,
предшествующего медианному.
Определение. Медианным интервалом называется тот интервал, в котором накопленная частота впервые окажется больше половины объёма выборки (n/2) или накопленная частость окажется больше 0,5.
Численные значения среднего, моды и медианы отличаются, когда имеет место несимметричная форма эмпирического распределения.
Характеристики рассеяния результатов измерений
Для математико-статистического анализа результатов выборки знать только характеристики положения недостаточно. Одна и та же величина среднего значения может характеризовать совершенно различные выборки.
Поэтому кроме них в статистике рассматривают также характеристики рассеяния (вариации, или колеблемости) результатов.