
- •Дніпропетровськ
- •Анализ взаимовлияния экономических факторов.
- •Принятие оптимальных решений при планировании, распределении материальных, трудовых и финансовых ресурсов.
- •Простейшие эконометрические модели функции спроса (d)
- •Модели функции d:
- •Эластичность функции
- •Виды эластичности спроса
- •Эластичность спроса (d) по доходу (I)
- •Функция предложения (s)
- •Модели функции s
- •Связь предельной прибыли и эластичности спроса по цене
- •Определение эластичности спроса по цене, если цена представлена функцией
- •Некоторые основные сведения из статистики
- •Оценки выборочной совокупности
- •Классы оценок:
- •Основные точечные оценки выборочной совокупности:
- •Проверка статистических гипотез
- •Этапы проверки статистических гипотез:
- •Доверительные интервалы
- •Модель линейной регрессии
- •Два типа взаимосвязи х и y:
- •Задачи регрессионного анализа:
- •Парная линейная регрессия
- •Парная линейная регрессия
- •I. Метод наименьших квадратов (мнк)
- •II. Оценка коэффициентов парной линейной регрессии
- •Уравнения задачи спецификации:
- •Оценка адекватности математической модели
- •Исследование коэффициента корреляции
- •Основные идеи t-статистики Стьюдента
- •Проверка общего качества уравнения регрессии. Коэффициент детерминации
Связь предельной прибыли и эластичности спроса по цене
Пусть Q – количество товара,
![]() –
цена на
товар, (тогда
–
цена на
товар, (тогда
![]() - спрос на товар,
т.е.
- спрос на товар,
т.е.
![]() ),
),
R(Q) – суммарная прибыль от реализации товара (выручка), которая определяется произведением проданного количества товара на цену:
![]()
Поведение функции
R
при росте её аргумента Q,
как известно, можно определить, исходя
из знака её производной
![]() (когда
(когда
![]() ,
функция
,
функция
![]() возрастает, когда
возрастает, когда
![]() – функция
убывает). Т.е. для нахождения ответа на
вопрос о росте или снижении суммарной
прибыли (выручки) достаточно определить
знак производной
,
которую назовём функцией предельной
прибыли.
– функция
убывает). Т.е. для нахождения ответа на
вопрос о росте или снижении суммарной
прибыли (выручки) достаточно определить
знак производной
,
которую назовём функцией предельной
прибыли.
Предельную прибыль находим по соотношению:
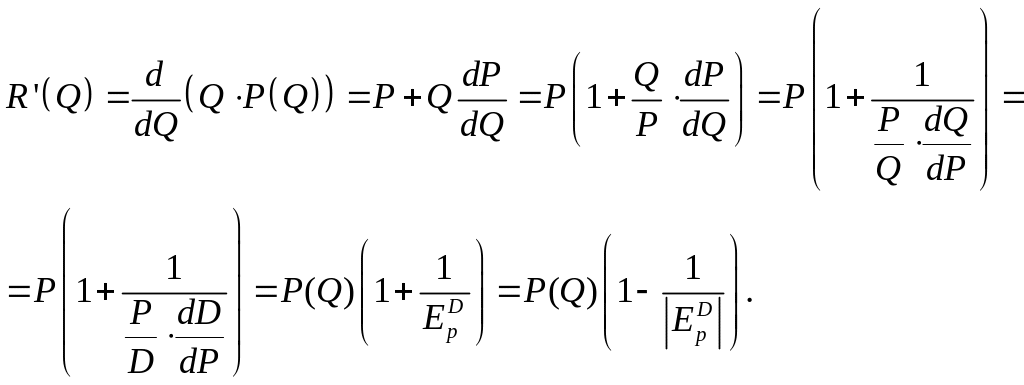
Проанализируем
знак полученного выражения (с учётом
того, что цена
![]() ).
Рассмотрим возможные случаи эластичности
спроса:
).
Рассмотрим возможные случаи эластичности
спроса:
При реализации товара неэластичного спроса
 дробь
дробь
 ,
выражение
,
выражение
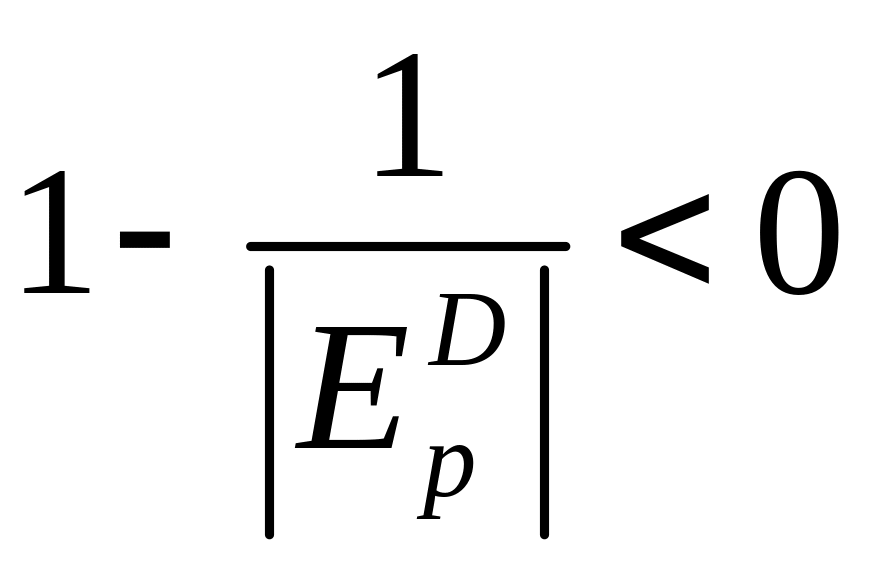 ,
тогда предельное значение прибыли
,
тогда предельное значение прибыли
 отрицательное и тогда суммарная прибыль
падает.
отрицательное и тогда суммарная прибыль
падает.При реализации товара эластичного спроса
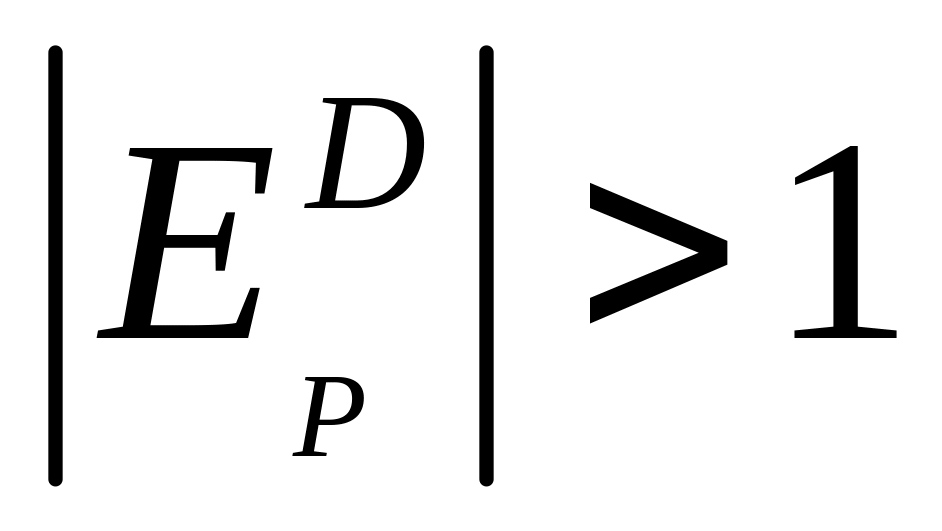 дробь
дробь
 ,
выражение
,
выражение
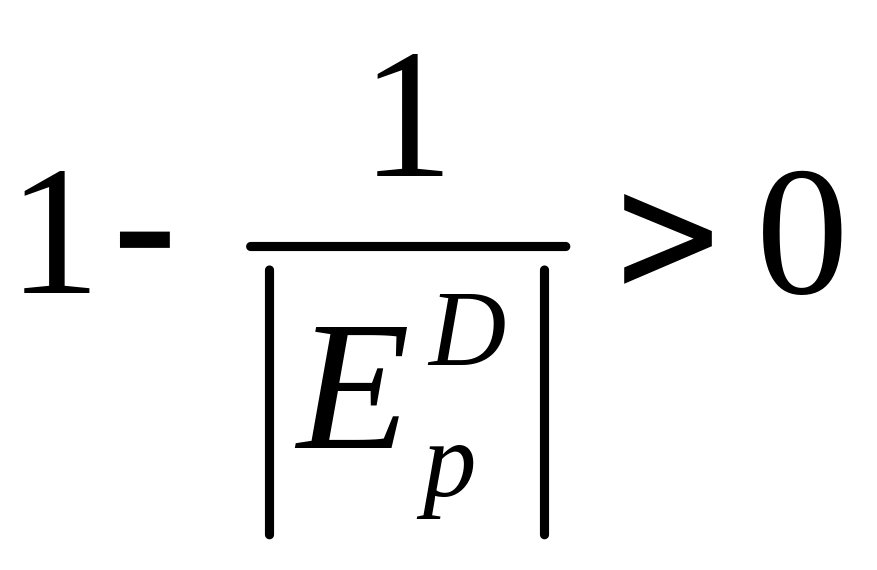 ,
тогда предельное значение прибыли
положительное и суммарная прибыль
увеличивается.
,
тогда предельное значение прибыли
положительное и суммарная прибыль
увеличивается.При реализации товара единичной эластичности спроса
 дробь
дробь
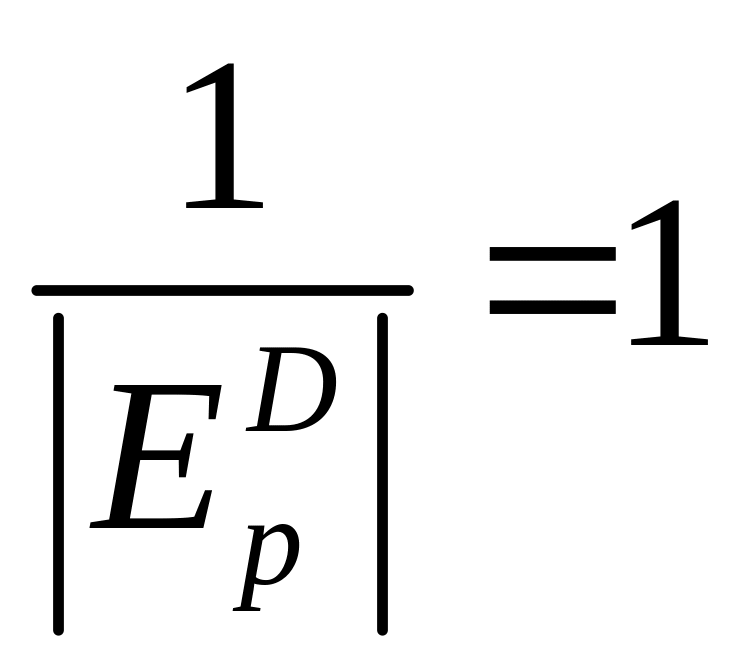 ,
выражение
,
выражение
 ,
тогда предельное значение прибыли
,
тогда предельное значение прибыли
 и суммарная прибыль
не изменяется ни при росте, ни при
падении цены.
и суммарная прибыль
не изменяется ни при росте, ни при
падении цены.
В этой связи особо ценным будет утверждение: для товаров эластичного спроса суммарная прибыль - функция возрастающая, а для товаров неэластичного спроса - убывающая.
Определение эластичности спроса по цене, если цена представлена функцией
Пусть цена на товар задана функцией . Тогда, как было отмечено ранее - спрос на товар, который является обратной функцией к функции , причём, .
Для того, чтобы определить функцию эластичности спроса
![]()
в этом случае, для
нахождения
![]() предварительно напомним из курса высшей
математики как находится производная
обратной функции.
предварительно напомним из курса высшей
математики как находится производная
обратной функции.
Пусть
![]() -
функция от аргумента x. Если в уравнении
y считать
аргументом, а x - функцией, то возникает
новая функция
-
функция от аргумента x. Если в уравнении
y считать
аргументом, а x - функцией, то возникает
новая функция
![]() ,
где
,
где
![]() - функция
обратная данной. Тогда
производная обратной функции равна
обратной величине производной данной
функции, т.е.
- функция
обратная данной. Тогда
производная обратной функции равна
обратной величине производной данной
функции, т.е.
![]()
Тогда, с учётом
сказанного, производная обратной функции
![]() будет иметь вид
будет иметь вид
 .
.
И функцию эластичности спроса перепишем тогда в виде:
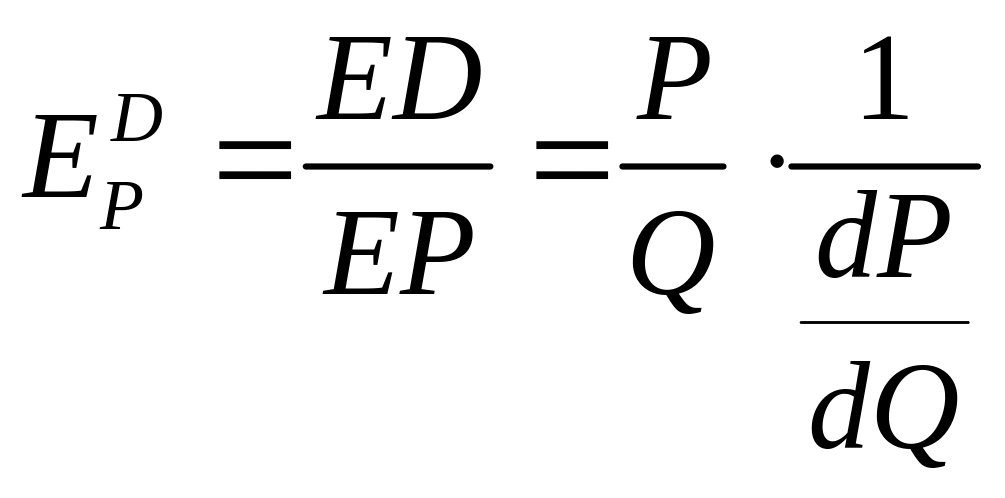
Некоторые основные сведения из статистики
Основополагающими в статистике являются два понятия:
— понятие массового явления;
— понятие совокупности.
Со статистической точки зрения не всякое множество может быть названо массовым явлением. Основной признак массового явления — вариация изучаемого фактора.
В этой связи массовое явление неразрывно связано со статистическими совокупностями.
Статистическая совокупность — некоторая совокупность объектов, сходная по определенным признакам.
Для статистической совокупности обязательно наблюдается вариация основных признаков. В общем случае все исследования и направлены на изучение некоторых признаков совокупности, которые отличают некоторые вариации. От полноты обследования единицы совокупности различают:
— генеральную совокупность;
— выборочную совокупность.
Совокупность явлений, из которых производится отбор части единиц называется генеральной совокупностью.
В то же время та часть единиц, которая выбрана из генеральной совокупности для исследования называется выборочной совокупностью (из генеральной совокупности 20000 пар обуви выбирают 20 пар обуви для эксперимента, с целью (например) определить среднее значение носки обуви — математическое ожидание).
Если выборочные значения расположить в порядке их возрастания, то такой ряд называется вариационным рядом:
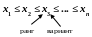
Порядковый номер варианта — ранг.
