Пример решения задачи на тему «растяжение и сжатие»

Построить по длине бруса, согласно схеме нагружения (рис. 1.1), эпюры продольных сил N, нормальных напряжений и перемещений поперечных сечений. Сделать вывод о прочности бруса, сравнив значения нормальных напряжений в опасном сечении с допустимым, если материал бруса — сталь 3 ( МПа, МПа).

Рисунок 1.1

Дано: F₁ =10 кН; F₂ =12 кН; F₃ =30 кН; S₁ = 200 мм²; S₂ = 300 мм²;

а = 0,3 м, b = 0,4 м.

Решение:

Имеем четыре участка нагружения (АВ, ВС, СD, DK), в пределах которых напряжения будут иметь постоянные значения.

Участок 1 (АВ). Рассечём, мысленно, стержень в местах, где необходимо определить значения внутренних усилий и внутренних напряжений. Одну из частей (левую) отбросим (рис. 1.2), а для оставшейся составим уравнение равновесия , заменив при этом действие отброшенной части на оставшуюся неизвестной внутренней силой N₁.

,

Рисунок 1.2

Тогда, кН.

Значение напряжений на участке: МПа.

Абсолютная деформация участка (относительные перемещения концов участка): мм.

Участок 2 (ВС).

,

кН.

МПа.

мм.

Участок 3 (DС).

,

кН.

МПа.

мм.

Участок 4 (KD).

,

кН.

МПа.

мм.

Для построения эпюры перемещений поперечных сечений, определим расстояния, на которые переместятся концы участков нагружения относительно жестко заделанного левого конца стержня (точки К).

Перемещение точки D относительно точки К:

_DK=l_KD=0,07 мм.

Тогда, перемещение точки С относительно точки К составит:

_СK=_DK +l_KD=0,07+0,18=0,25 мм.

Аналогично определим перемещения остальных концов участков:

_ВK=_СK +l_ВС=0,25+0,22= 0,47 мм,

_АK=_ВK +l_АВ=0,47+0,45= 0,92 мм.

Построив и проанализировав эпюры продольных сил N, нормальных напряжений и перемещений поперечных сечений (рис. 1.3), делаем вывод, что опасным участком вала является участок ВС с σ_max= 150 МПа.

Т.к. σ_max  [σ], то условие прочности выполняется.

Определим степень загруженности стержня:

.

Стержень нагружен на 62,5 %.

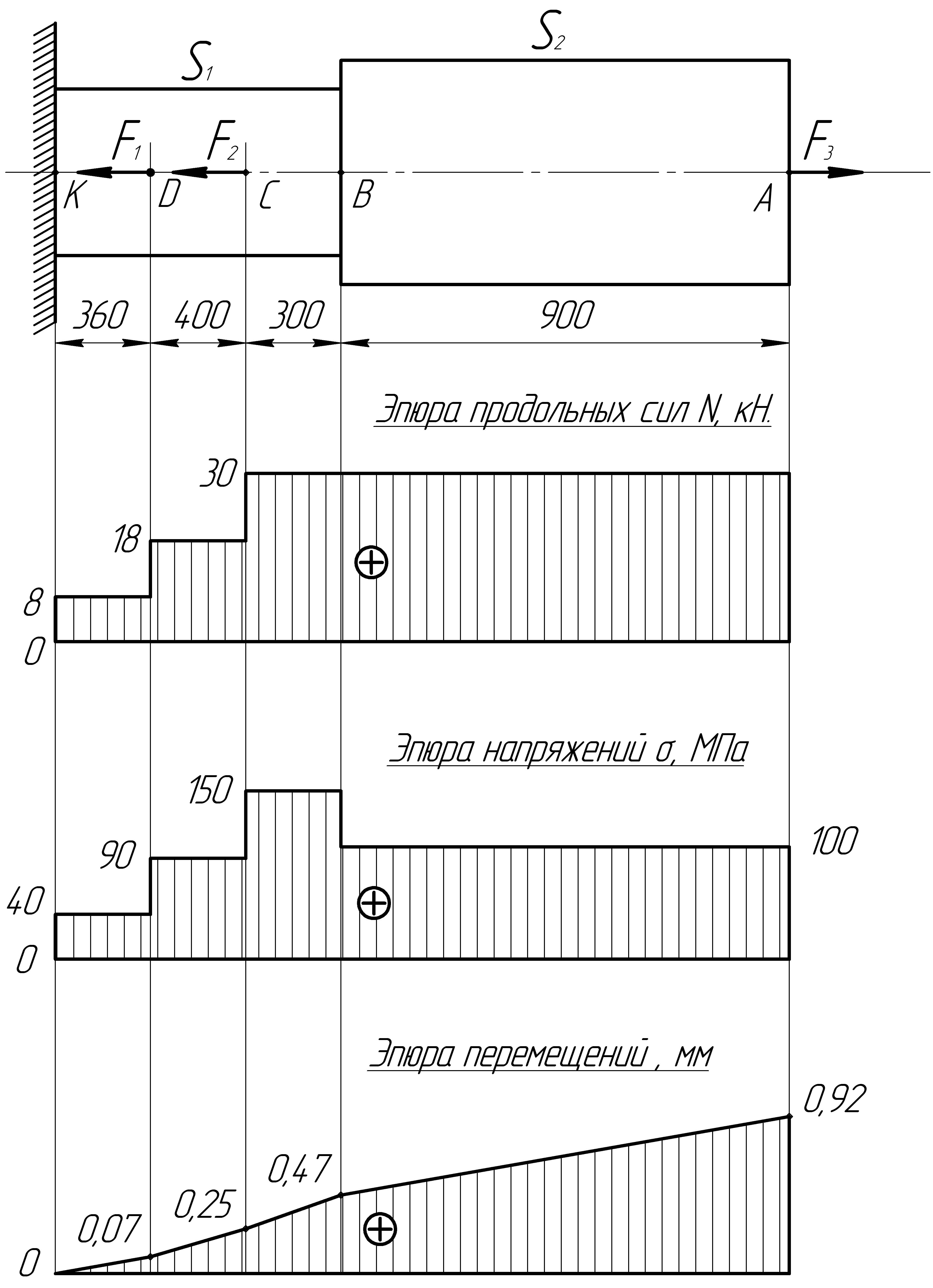
Рисунок 1.3

2. Определение геометрических характеристик поперечного сечения

При расчетах на прочность, жесткость и устойчивость используются геометрические характеристики поперечного сечения бруса: площадь, осевые и полярный моменты инерции, осевые и полярный моменты сопротивления. Кроме того, при их определении вспомогательную роль играют статические моменты и центробежные моменты инерции сечения.

Напомним определения, свойства и методы вычисления перечисленных характеристик (рис. 2.1).

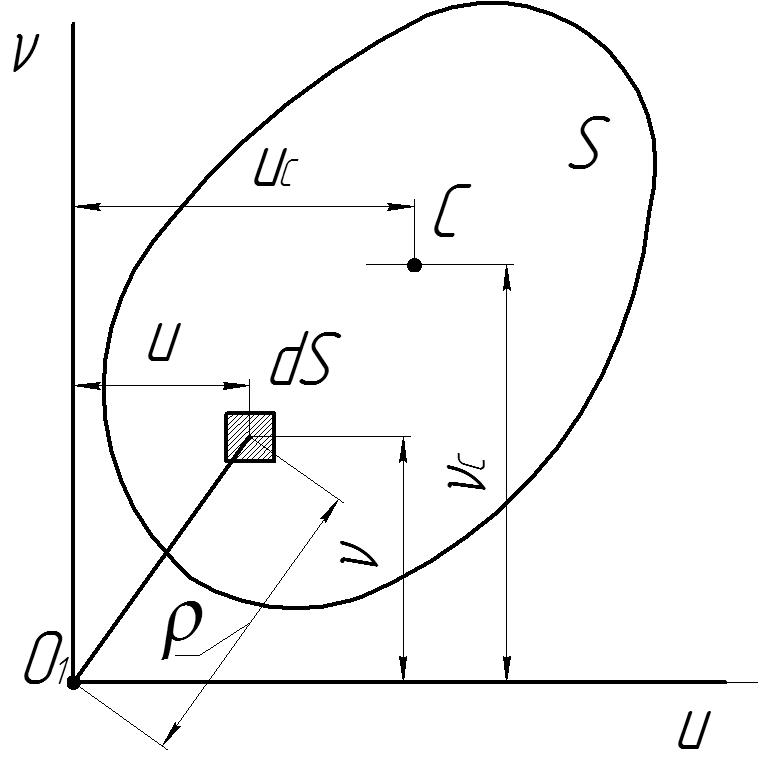
Рисунок 2.1

Площадь сечения . , где dS – площадь элементарной площадки.

Статический момент площади сечения – сумма произведений площадей элементарных площадок на их расстояния до данной оси, взятая по всей площади сечения. Статический момент сечения измеряется в единицах длины третьей степени (мм³, см³, м³).

Статические моменты сечения относительно осей Ои и Оv:

,

.

где и – расстояния от центра тяжести сечения соответственно до осей Оv и Ои.

Статический момент сечения может быть как положительным, так и отрицательным. Относительно любой оси, проходящей через центр тяжести сечения, он равен нулю.

Осевой момент инерции сечения – сумма произведений площадей элементарных площадок на квадраты их расстояний до данной оси, взятая по всей площади сечения.

;

.

Полярный момент инерции – сумма произведений площадей элементарных площадок на квадраты их расстояний до точки (полюса), взятая по всей площади сечения.

.

Осевые и полярный моменты инерции – величины существенно положительные. Осевые и полярные моменты инерции сечения измеряются в единицах длины четвертой степени (мм⁴, см⁴, м⁴).

Центробежный момент инерции – сумма произведений площадей элементарных площадок на их координаты, взятая по всей площади сечения.

.

Центробежный момент инерции измеряется в единицах длины четвертой степени (мм⁴, см⁴, м⁴), может быть положительным, отрицательным и равным нулю.

Через любую точку, взятую в плоскости сечения, можно провести две взаимно перпендикулярные оси, относительно которых центробежный момент инерции сечения равен нулю. Эти оси называются главными осями (иногда их называют главными осями инерции). Практический интерес представляют лишь главные оси, проходящие через центр тяжести сечения, они называются главными центральными осями (для краткости в дальнейшем будем в большинстве случаев называть их просто главными осями).

Осевые моменты инерции относительно главных осей (главные моменты инерции) экстремальны – относительно одной из них момент инерции максимален, а относительно другой – минимален. Для расчетов на прочность и жесткость при изгибе, сочетании изгиба с растяжением и в ряде других случаев нужно знать положение главных центральных осей и величины соответствующих моментов инерции.

В случае, если сечение имеет хотя бы одну ось симметрии, то эта ось и ось к ней перпендикулярная, проходящая через центр тяжести сечения, являются главными центральными осями.

При вычислении главных моментов инерции сечений, составленных из простейших геометрических фигур или стандартных прокатных профилей, широко применяются формулы перехода от центральных к параллельным им нецентральным осям (рис. 2.2).

Рисунок 2.2

Эти формулы имеют следующий вид: для осевого момента инерции

;

для центробежного момента инерции

.

Координаты а и b должны быть подставлены со своими знаками (а и b – координаты начала новой системы координат в старых осях). В частном случае, если исходные оси Ох₀ и Оу₀ главные, тогда имеем:

.

Приведем формулы для вычисления моментов инерции прямоугольника, треугольника, круга и кольца.

А. Прямоугольник (рис. 2.3): , где b ‑ сторона, параллельная оси, относительно которой вычисляется момент инерции.

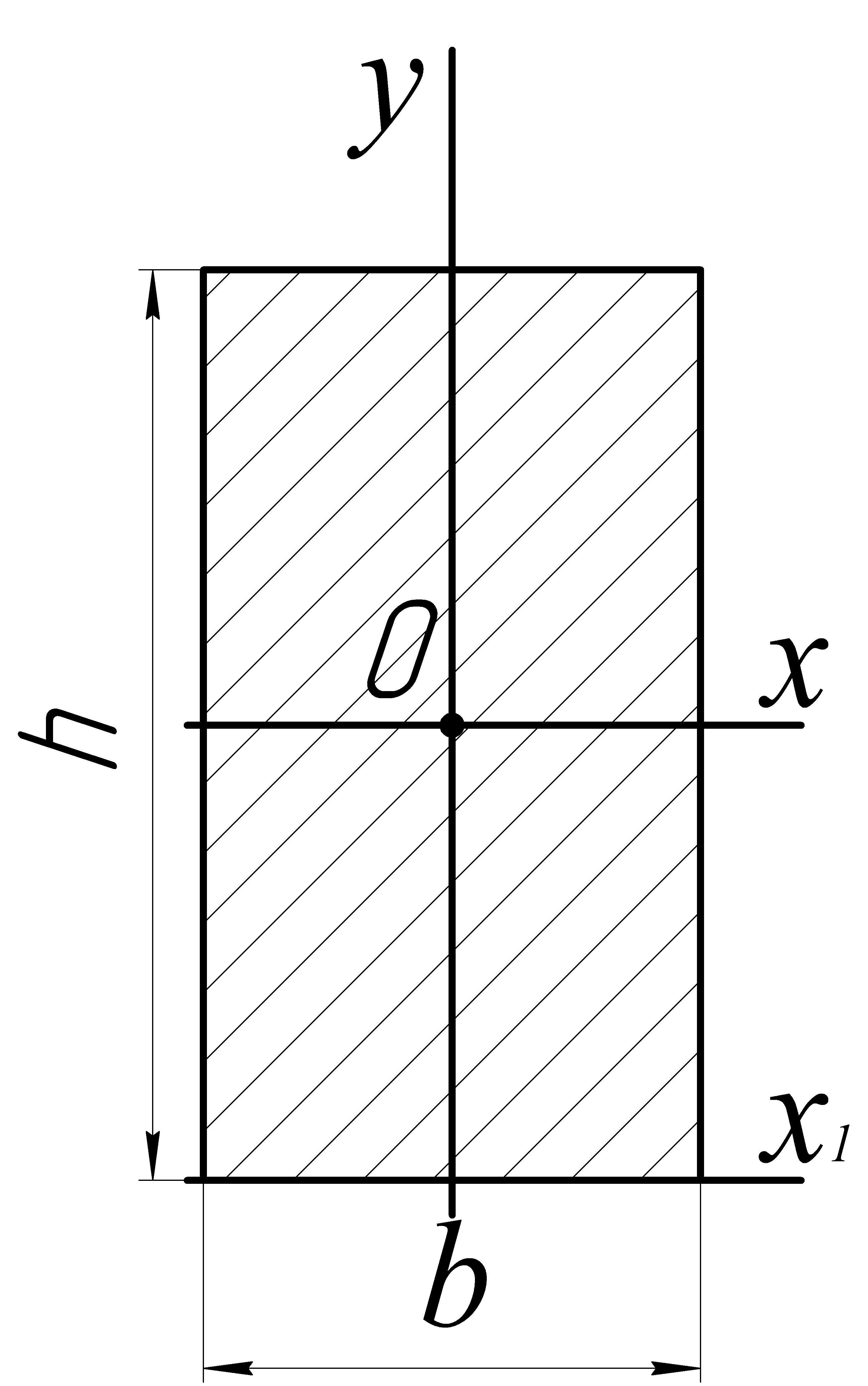
Рисунок 2.3

Для оси, совпадающей с одной из сторон прямоугольника (не главный момент инерции): .

Б. Равнобедренный треугольник (рис. 2.4).

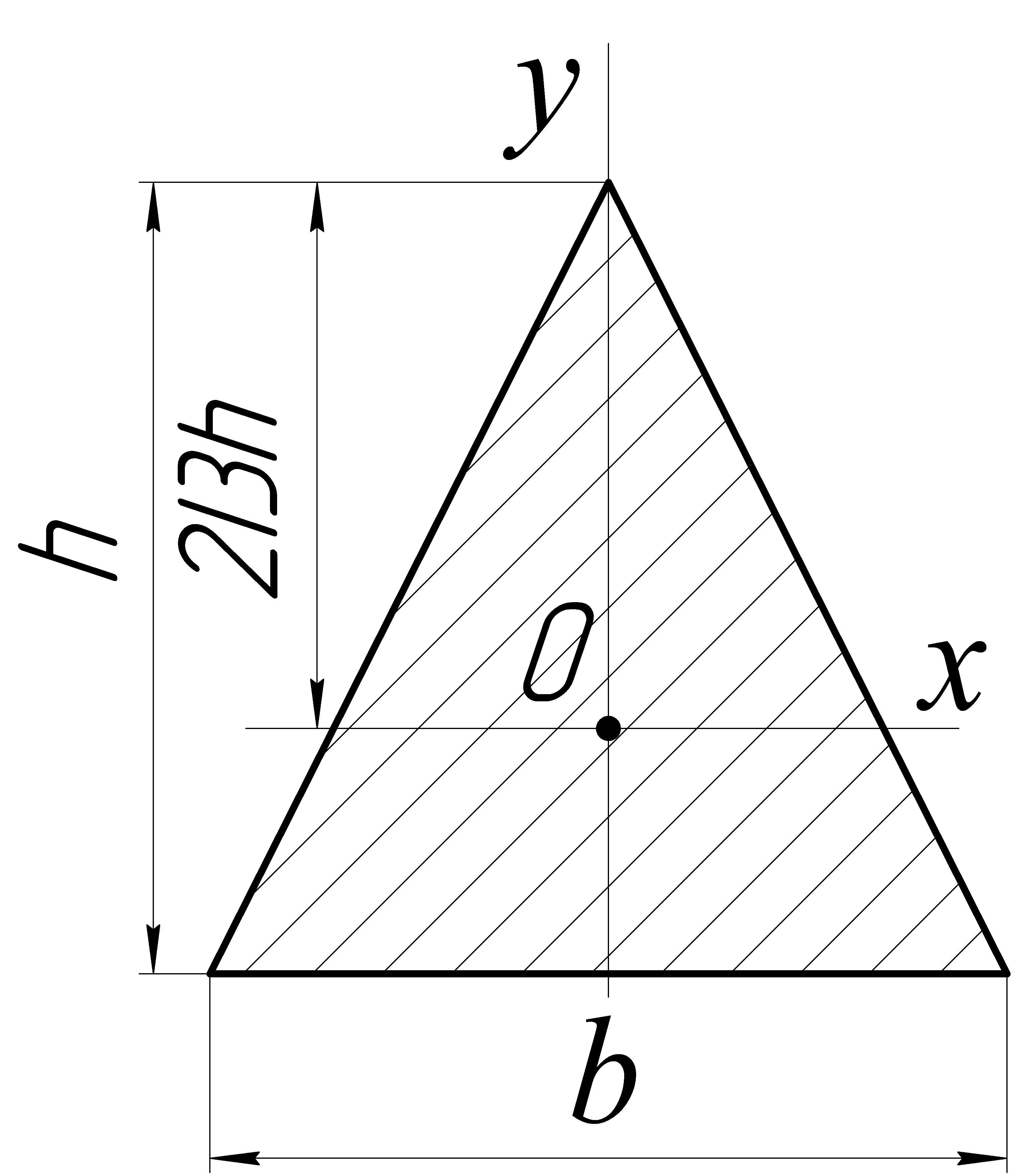
Рисунок 2.4

Главные моменты инерции: ; .

Заметим, что формула дает величину момента инерции любого треугольника относительно оси, параллельной его основанию, но, если треугольник неравнобедренный, указанная ось не будет главной.

В. Круг (рис. 2.5):

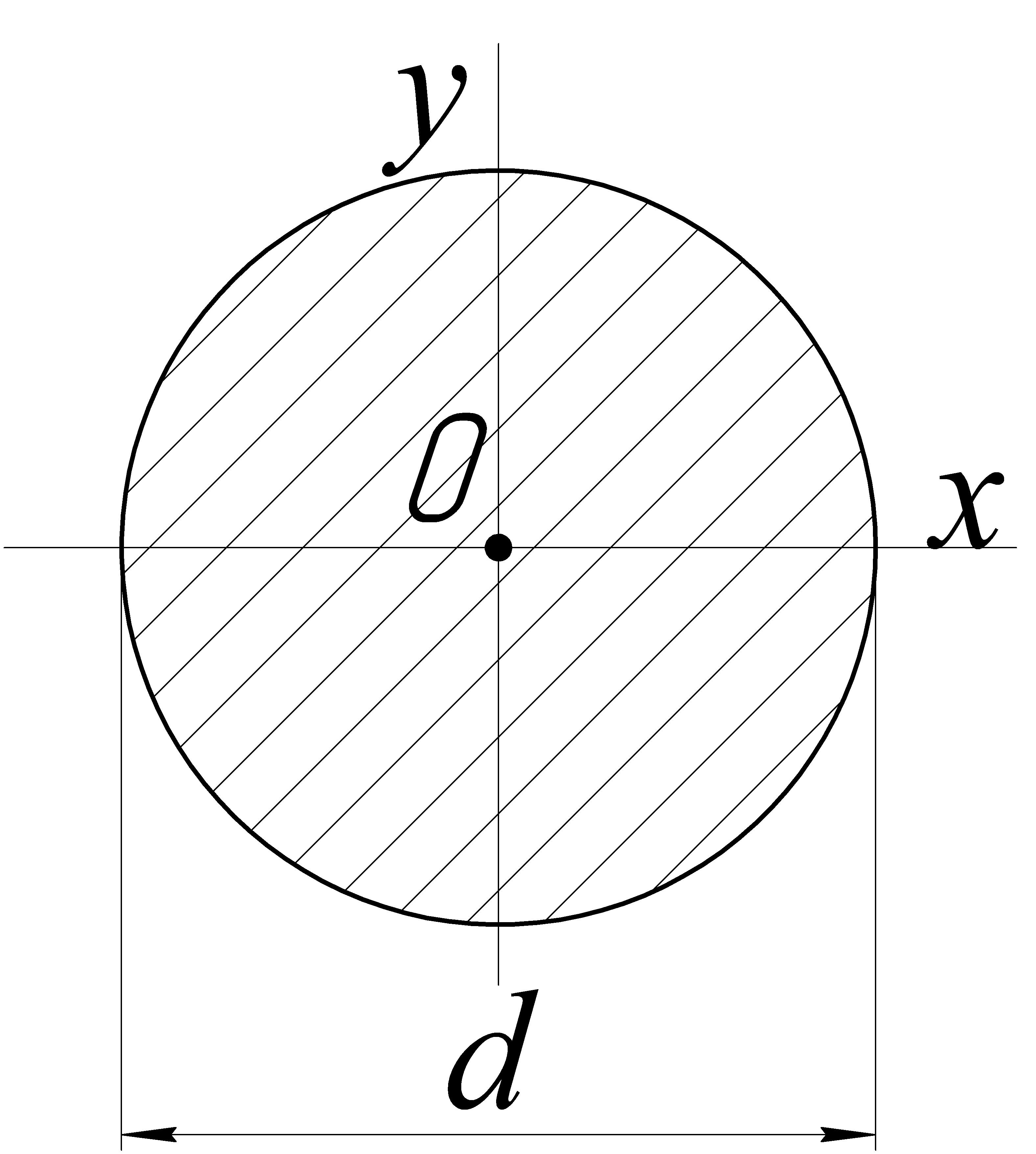
Рисунок 2.5

Г. Кольцо (рис. 2.6): , где: , коэффициент трубы.

Рисунок 2.6.

Заметим, что для круга и кольца все центральные оси главные и моменты инерции относительно этих осей равны между собой. Этим же свойством обладает любое сечение, у которого два главных центральных момента инерции одинаковы.

При вычислении моментов инерции сложных сечений (составленных из простейших фигур или прокатных профилей) координаты их центра тяжести определяют по формулам:

^;

^,

где: ; ; – соответственно площадь и координаты центра тяжести каждой из составляющих фигур; S; ; ‑ площадь и статические моменты всего сечения.

Моменты инерции (осевые и центробежные) сложных сечений относительно данных осей определяют путем суммирования соответствующих моментов инерции составляющих фигур относительно тех же осей.

При этом используются формулы перехода от центральных к параллельным им нецентральным осям.

В тех случаях, когда сечение не имеет ни одной оси симметрии, сначала вычисляют моменты инерции относительно некоторых целесообразно выбранных центральных осей Ох₀ и Оу₀ (исходные оси), затем определяют угол наклона главных осей по отношению к исходным и величины главных моментов инерции.

Связь между моментами инерции относительно исходных осей (Ох₀, Оу₀) и осей, повернутых на произвольный угол а (рис. 2.7), имеет вид:

;

.

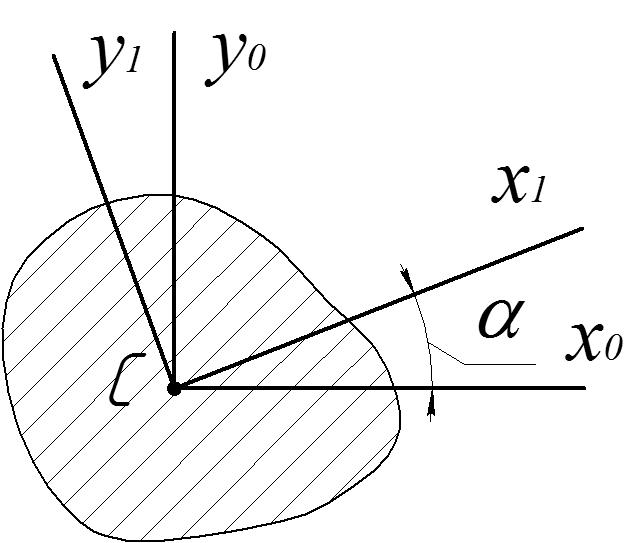
Рисунок 2.7

Угол поворота главных осей по отношению к исходным определяется из зависимости

.

Эта формула дает два значения угла : и = + 90°. При > , угол дает положение главной оси, относительно которой момент инерции максимален. Положительный угол следует откладывать от оси х₀ против хода часовой стрелки.

Для определения положения (угла наклона) главных осей можно применять формулы:

;

,

где: , и , – углы, образуемые главными осями х и у соответственно с осью х₀; и – главные моменты инерции.

Главные моменты инерции можно вычислить, подставляя в нее последовательно = и = , но практически удобнее пользоваться формулами, не содержащими тригонометрических функций. Эти формулы имеют вид:

;

.