Техника финансовых вычислений при помощи Excel

Пять платежей по три рубля каждый нужно внести по схеме пренумерандо. Получатель аннуитета использует эти средства с доходностью R = 8% за период между платежами.

Какова будущая стоимость FV этого срочного аннуитета (срок n = 5) в конце пятого периода в результате начисления процентов на все поступившие платежи? Обозначим размер одного платежа буквой A. Тогда

В условиях нашего примера поток платежей пренумерандо позволяет их получателю накопить сумму 19,01 руб., а в случае аннуитета постумерандо она бы составила только 17,60 руб.

На рисунке ниже показана схема вычисления будущей стоимости каждого платежа и аннуитета пренумерандо в конце срока.

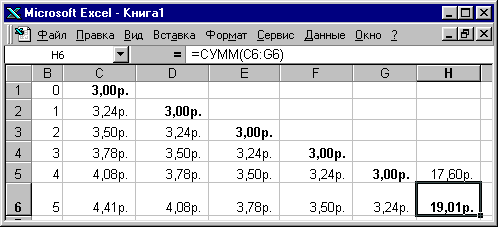
Какую сумму достаточно вложить на 5 периодов с начислением 8% сложных, чтобы в конце срока снять 19,01 руб.?

Текущая стоимость бессрочного аннуитета (вечной ренты при бесконечно большом сроке n) есть сумма всех членов бесконечно убывающей геометрической прогрессии со знаменателем 1/(1+R), которая при R < –2 или R > 0 сходится.

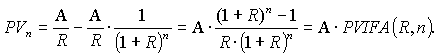
Эквивалентная ей в конце срока будущая стоимость срочного аннуитета постумерандо есть

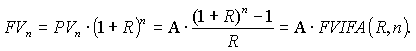
Процентный множитель будущей стоимости аннуитета FVIFA(R,n) – Future Value Interest Factor of Annuity является основным финансовым коэффициентом, который показывает, какую сумму можно накопить, постоянно получая выплаты единичного размера в течение срока n при начислении R % сложных за каждый период на уже аккумулированные денежные средства.

Процентный множитель текущей стоимости аннуитета PVIFA(R,n) – Present Value Interest Factor of Annuity также является финансовым коэффициентом, и показывает, какую сумму достаточно инвестировать в начальный момент времени, чтобы потом регулярно в течении срока, состоящего из n процентных периодов получать платежи единичного размера с учетом начисления на оставшиеся денежные средства R% сложных за период.

Знакомство с условностями автоматизации финансовых расчетов в среде процессора электронных таблиц начнем со встроенной функции =FV(rate; nper; pmt; pv; type)

=БЗ(норма; число_периодов; выплата; нз; тип) в исходной русификации

=БС(ставка; кпер; плт; пс; тип) в новейшей русификации.

Пример:

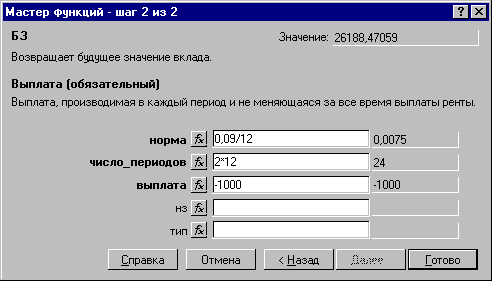
Господин Иванов в конце каждого месяца переводит 1000р. за счет в банк, начисляющий ежемесячно сложные проценты по номинальной ставке 9% годовых. Какая сумма накопится на счете за два года, при сохранении на это время всех указанных условий без изменения?

На рисунке ниже показано применение функции БЗ(БС)=FV для расчета будущей стоимости аннуитета.

Аннуитетные финансовые функции в русификации:

Показатель	Встроенная функция Excel
Будущее значение/Будущая стоимость	БЗ/БС(ставка;кпер;плт;пс;тип)
Future value	FV(rate;nper;pmt;pv;type)
Настоящая стоимость	ПС(ставка;кпер;плт;бс;тип)
Present value	PV(rate;nper;pmt;fv;type)
Периодический (аннуитетный) платеж	ПЛТ(ставка;кпер;пс;бс;тип)
Payment	PMT(rate;nper;pv;fv;type)
Количество периодов	КПЕР(ставка;плт;пс;бс;тип)
Number of periods	NPER(rate;pmt;pv;fv;type)
Процентная ставка	СТАВКА(кпер;плт;пс;бс;тип;предположение)
Interest rate	RATE(nper;pmt;pv;fv;type;guess)

Выполним расчет будущей стоимости аннуитета поэтапно. Ниже в восьмой строке таблицы рабочего листа дан формат вызова функции =БС, возвращающий то же самое числовое значение, которое в ячейке седьмой строки найдено по рекуррентным формулам.

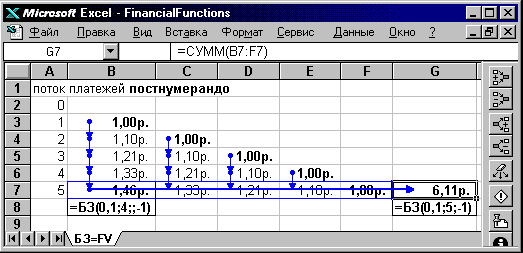
В зависимости от выбора пользователем из полного списка аргументов встроенной функции =БС(норма; число_периодов; выплата; нз; тип) подмножества тех аргументов, значения которых известны в задаче, можно с помощью одной и той же функции посчитать и наращенную сумму вклада, и будущую стоимость аннуитета, причем с переключением формул между типами потоков платежей постнумерандо и пренумерандо.

Рассмотрим полностью возможные варианты.

1,46 р. = FV(0,1;4;0;-1;0) =FV(0,1;4;0;-1;0) =FV(0,1;4;;-1) – будущая стоимость одного вложенного рубля (нз=-1) после четырех раз (число_периодов=4) присоединения к нему процентных денег, начисляемых в конце периода по ставке сложных процентов 10% (норма=0,1) без дополнительных поступлений и выплат. В связи с полным отсутствием в течение срока промежуточного потока платежей нет смысла уточнять и момент их поступления в нулевом размере (тип=0, значение используется по умолчанию).

1,61 р. =FV(0,1;5;0;-1;0) =FV(0,1;5;0;-1;0) =FV(0,1;5;;-1) – будущая стоимость одного вложенного рубля (нз=-1) после пяти раз (число_периодов=5) присоединения к нему процентных денег, начисляемых в конце периода по ставке сложных процентов 10% (норма=0,1) без дополнительных поступлений и выплат (выплата=0, тип=0).

6,11 р. = FV(0,1;5;-1;0;0) = FV(0,1;5;-1;0;0) =FV(0,1;5;-1) – будущая стоимость потока пяти периодических платежей (число_периодов=5) единичного размера, вносимых (выплата=-1) регулярно в конце периода (потоку постнумерандо соответствует тип=0, значение используется по умолчанию) при начислении 10% сложных (норма=0,1) за период между моментами внесения платежей на поступившие ранее средства.

6,72 р. = FV(0,1;5;-1;0;1) FV(0,1;5;-1;0;1) =FV(0,1;5;-1;;1) – будущая стоимость потока пяти периодических платежей (число_периодов=5) единичного размера (выплата=-1), поступающих в начале периода (потоку пренумерандо соответствует тип=1) при начислении за каждый период между платежами 10% сложных (норма=0,1).

Пример: Молодой человек c пятнадцатилетнего возраста в конце каждого месяца регулярно вносит по 15 долл. на сберегательный счет в банк, начисляющий на всю растущую сумму сложные проценты по номинальной ставке 15% годовых. В каком возрасте этот человек может стать миллионером?

Выразим срок (число периодических платежей) из формулы будущей стоимости аннуитета:

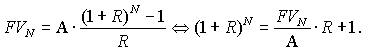
Используя определение и свойства логарифма, самостоятельно продолжите вывод формулы срока накопления миллиона в условиях задачи и найдите ответ на поставленный вопрос.

На рисунке ниже Применение функции КПЕР=NPER для определения срока аннуитета.

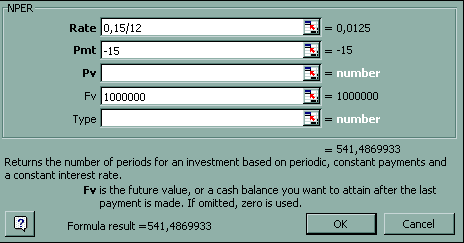
Найденный срок выражен в месяцах. 542/12=45 полных лет, так что сумма 15+45 дает искомый в задаче возраст 60 лет.

Какую сумму достаточно вложить на такой же срок единовременно, чтобы при той же доходности при ежемесячном начислении сложных процентов накопить 1 млн.долл.?

Ответ: -1190,948=PV(0,15/12;542;;1000000).

При какой годовой процентной ставке удастся накопить миллион к 55 годам?

Ответ: 17,3% =RATE((55-15)*12;-15;;1000000)*12.

При каком размере ежемесячного платежа удастся накопить миллион к 50 годам без изменения ставки 15%?

Ответ: -68,13 долл.= PMT(0,15/12;(50-15)*12;;1000000).

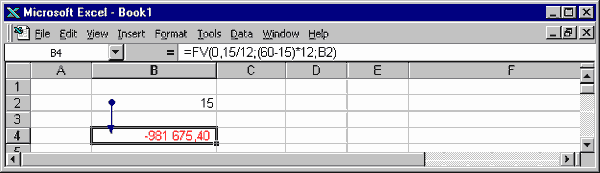
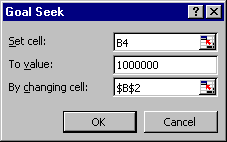
Варьировать параметры задачи можно и неявно, подгоняя влияющие исходные данные, например, размер ежемесячного платежа, под искомую будущую стоимость 1 млн.долл.

Подбор значения будущей стоимости аннуитета изменением размера платежа.