Iэфф – эффективная ставка

Из указанной выше формулы легко выводится iэфф в качестве искомого.

Пример:

Некая сумма размещена под 8% с ежеполугодичным начислением. Найти эффективную ставку.

Решение:

PV(1+0,08/2)² = 1,0816*PV

1,0816*PV = PV(1+iэфф)

1,0816 = 1+iэфф

Iэфф = 0,0816, т.е. 8,16%

Пример:

Сумма размещена под 7% годовых с ежеквартальным начислением. Найти эффективную ставку.

Решение:

PV(1+0,07/4)⁴ = 1,0719*PV

Найдём iэфф:

1,0719*PV = PV(1+iэфф)

1,0719 = 1+iэфф

Iэфф = 0,0719, т.е. 7,19%

Пример:

При выдаче кредита на 7 лет под 30% годовых были удержаны комиссионные. Сложные проценты начислялись ежегодно на исходную величину кредита. Сколько процентов составили комиссионные от величины кредита, если доходность такой финансовой операции для банка в виде iэфф = 31,2%

Решение:

PV(1+0,3) = 6,275*PV

6,275*PV+x*PV = PV(1+0,312)⁷

6,275*PV+x*PV = 6,692*PV

x*PV = 0,417*PV

х = 0,417, т.е. 41,7%

Задачи для самостоятельного решения:

1. квартира стоит 80 тыс. у.е, через 2 года её стоимость составит 125 тыс. у.е. Найти стоимость квартиры через 1 год в день своего рождения по трём различным способам начисления процентов:

• простое начисление процента

• сложное начисление процентов с ежемесячным удорожанием (начислением)

• сложное начисление процентов с ежеквартальным удорожанием.

2. по контракту заемщик должен уплатить кредитору 1500 тыс.д.е. через 3 года и 1000 тыс.д.е. через 5 лет, считая от момента заключения контракта. Заемщик предложил уплатить 1100 тыс.д.е. через 4 года и 1400 тыс.д.е. через 5 лет. Эквивалентны ли эти контракты?

3. банк выплачивает по вкладам 10% сложных годовых. Какова реальная доходность вкладов при начислении процентов: а) ежемесячно; б) ежеквартально; в) по полугодиям.

4. каковы будут эквивалентные номинальные процентные ставки с полугодовым начислением процентов и ежемесячным начислением процентов, если соответствующая им эффективная ставка должна быть равна 25%?

5. решено консолидировать два платежа со сроками 20.04 и 10.05 и суммами платежа 20 тыс. руб. и 30 тыс. руб. Срок консолидации платежей 31.05. Определить сумму консолидированного платежа при условии, что ставка равна 10% годовых.

6. предлагается платеж в 45 тыс. руб. со сроком уплаты через 3 года заменить платежом со сроком уплаты через 5 лет. Найти новую сумму платежа, исходя из процентной ставки 12 % годовых.

Домашнее задание:

Придумать самостоятельно 4 задачи на нахождение переменных в условиях эквивалентности.

Функции сложного процента

Аннуитет — это денежный поток, в котором все суммы возникают не только через одинаковые промежутки времени, но и равновеликие. Таким образом, аннуитет — это денежный поток представленный одинаковыми суммами. Аннуитет может быть исходящим денежным потоком по отношению к инвестору (например, осуществление периодических равных платежей), либо входящим денежным потоком (например, поступление арендной платы, которая обычно устанавливается одинаковой фиксированной суммой).

Изложение и восприятие данного материала целесообразно с использованием шести функций сложных процентов с соответствующими пиктограммами, каждая из которых содержит:

• номер функции в соответствии с колонками таблиц сложных процентов - подробнее о таблицах сложных процентов Вы можете узнать в разделе "Сложный процент" (в левом верхнем углу);

• краткую аббревиатуру (левый верхний угол)

• название функции в Microsoft Excel (в правом верхнем углу в скобках);

• графическую интерпретацию математического преобразования, осуществляемого при помощи функции (в центре);

• название функции (внизу).

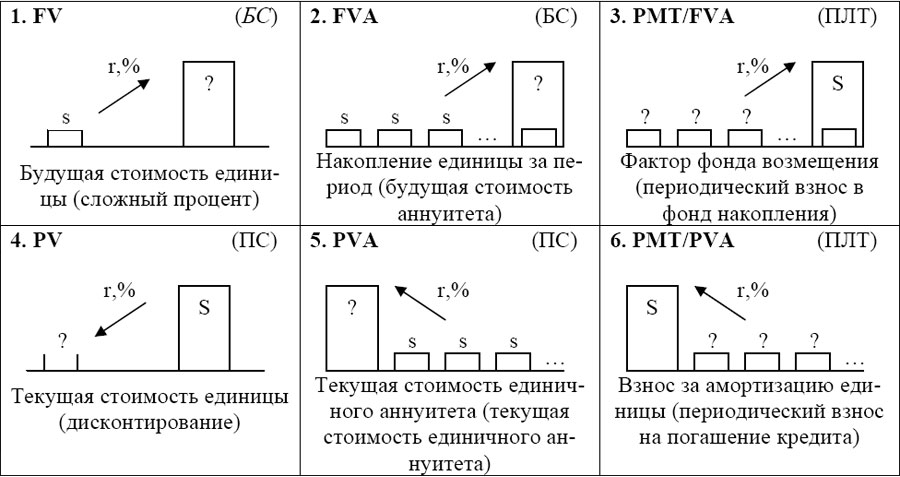
S и s - известные величины единичных денежных потоков, и входящих в состав аннуитета. Знаком "?" обозначены неизвестные искомые величины.

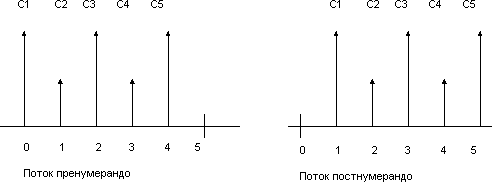
Если специально не оговорено, предполагается, что денежные потоки расположены в конце соответсвующего временого интервала.

Тем не менее, существует понятие пренумерандо – расположение платежей в начале периода и постнумерандо – в конце периода. Наглядно это показано в схемах:

Последовательность рассмотрения функций не совпадает с приведенной нумерацией в методических целях. Следует также обратить внимание на то, что название функций и их аббревиатура имеют разночтения в литературе, что, впрочем, не влияет на содержательную сторону вопроса. Детальное описание работы и применения функций сложного процента описаны в соответсвующих разделах.

Следует отметить, что в рамках практических занятий будут рассмотрены задачи, в условиях которых фигурирует ставка в 8% годовых с различными видами начисления, а период начисления не будет превышать 3 года.

Справочная таблица со значениями сомножителей, соответствующих всем шести функциям приведена ниже:

Таблицы шести функций сложного процента при ежегодном начислении процента
Год	Будущая стоимость единицы	Будущая стоимость единичного аннуитета	Коэффициент фонда возмещения	Настоящая стоимость единицы	Настоящая стоимость единичного аннуитета	Взнос на амортизацию единицы
1	1,0800	1,0000	1,0000	0,9259	0,9259	1,0800
2	1,1664	2,0800	0,4808	0,8573	1,7833	0,5608
3	1,2597	3,2464	0,3080	0,7938	2,5771	0,3880
Таблицы шести функций сложного процента при ежемесячном начислении процента
Год	Будущая стоимость единицы	Будущая стоимость единичного аннуитета	Коэффициент фонда возмещения	Настоящая стоимость единицы	Настоящая стоимость единичного аннуитета	Взнос на амортизацию единицы
1	1,0830	12,4499	0,0803	0,9234	11,4958	0,0869
2	1,1729	25,9332	0,0386	0,8526	22,1105	0,0452
3	1,2702	40,5356	0,0247	0,7873	31,9118	0,0313

1. Будущая стоимость единицы. FV (БСЕ) Функция позволяет определить будущую стоимость суммы, которой располагает инвестор в настоящий момент, исходя из предполагаемой ставки дохода, срока накопления и периодичности начисления процентов.

FV = PV (1+i/m)^n*m, где FV – будущая стоимость PV – настоящая стоимость

i - процентная ставка

n – количество периодов начисления

m - количество начислений за период

Пример:

Выдан кредит на сумму 4000 у.е. сроком на 3 года под 8% годовых ежегодного начисления с погашением в конце периода. Найти сумму погашения.

Решение:

P*БСЕ на 3-ий год при ежегодном начислении

4000*1,2597 = 5038,8 у.е.

2. Настоящая стоимость единицы. PV (НСЕ) Данная функция является обратной по отношению к функции «будущей стоимости единицы» (сложный процент) и определяется путем её обращения. Позволяет определить текущую стоимость суммы, которой будет располагать инвестор в определённый момент в будущем, исходя из предполагаемой ставки дохода, срока накопления и периодичности начисления процентов.

PV = FV/(1+i/m)^n*m

Пример:

На Ваш расчётный счёт через 2 года поступит 17000$. Сколько сегодня можно взять в кредит по 8% годовых с ежемесячным начислением?

Решение:

F*НСЕ на 2-ой год при ежемесячном начислении.

17000*0,8526 = 14494,2$

3. Будущая стоимость единичного аннуитета. FVA (БСЕА) Функция позволяет определить будущую стоимость суммы, полученной от ряда платежей (PMT-размер одного платежа) за определённый период времени, исходя из предполагаемой ставки дохода, срока накопления и периодичности начисления процентов.

Данная функция, характеризует будущую стоимость аннуитета, отличается от FV только тем, что проценты начисляются не на однократно вложенную сумму, а на периодические равновеликие взносы, производимые в течении n периодов.

FVA = [(1+i)ⁿ-1]/i

Пример:

Через 2 года нужно произвести ремонт на сумму 2,5 тыс. $. Для этого ежегодно перечисляется по 1,2 тыс. $ на расчётный счёт. Достаточно ли этих средств?

Решение:

PMT*БСЕА на 2-ой год при ежегодном начислении.

1,2*2,0800 = 2,496 тыс. $

Ответ: не достаточно!

4. Настоящая стоимость единичного аннуитета. PVA (HСЕА) Функция позволяет определить настоящую стоимость суммы, получаемой от ряда платежей в будущем (PMT-размер одного платежа) за определённый период времени, исходя из предполагаемой ставки дохода, срока накопления и периодичности начисления процентов.

Данная функция, характеризует текущую стоимость аннуитета, отличается от PV только тем, что проценты начисляются не на однократно вложенную сумму, а на периодические равновеликие взносы, производимые в течении n периодов.

PVA = [1-(1+i)^-n]/i

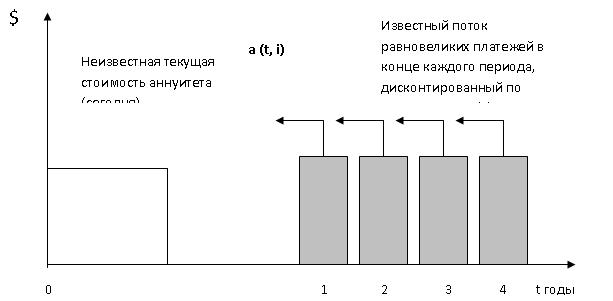
Пример:

На расчётный счёт ежемесячно поступает по 1000 $. Определить текущую стоимость потока продолжительностью в 2 года.

Решение:

PMT*НСЕА на 2-ой год при ежемесячном начислении.

1000*22,1105 = 22110,5 $

5. Коэффициент фонда возмещения. SFF (КФВ) Функция позволяет определить размер одного платежа (PMT) при известной будущей стоимости всего ряда (FVA), исходя из предполагаемой ставки дохода, срока накопления и периодичности начисления процентов. Данная функция является обратной по отношению к функции "Будущей стоимости единицы" (FVA).

SFF = 1/FVA = i/[(1+i)ⁿ-1]

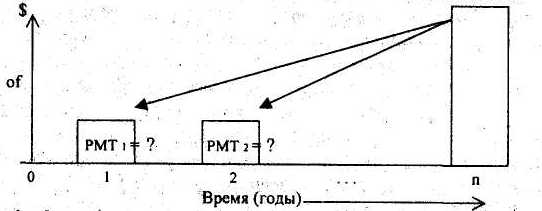
Пример:

Какую сумму необходимо ежемесячно откладывать на счёт под 8% годовых, чтобы к концу 3-его года накопить 2000 у.е.?

Решение:

FVA*КФВ на 3-ий год при ежемесячном начислении

2000*0,0247 = 49,4 у.е.

6. Взнос на амортизацию единицы. PMT/PVA (ВАЕ) Функция позволяет определить размер одного платежа (PMT) при известной настоящей стоимости всего ряда (PVA), исходя из предполагаемой ставки дохода, срока накопления и периодичности начисления процентов. Данная функция является обратной по отношению к функции "Настоящей стоимости единицы" (PVA).

PMT/PVA = 1/PVA = i/[1-(1+i)^-n]

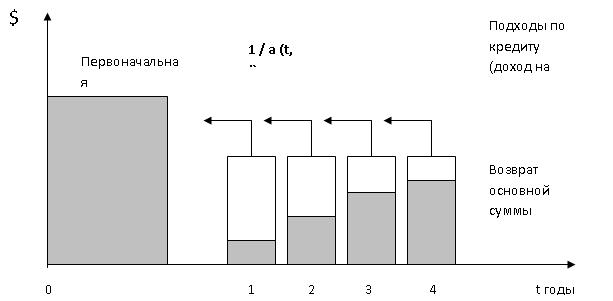
Пример:

Какую сумму необходимо ежегодно направлять на погашение кредита за квартиру стоимостью 250 тыс. у.е., взятого под 8% годовых на 2 года?

Решение:

PVA*ВАЕ на 2-ой год при ежегодном начислении

250*0,5608 = 140,2 тыс. у.е.

Задачи для самостоятельного решения:

1. Сколько надо внести на р/с, чтобы через три года накопить 18 тыс. (8% ежемес. нач.)

2. Банк выдал кредит 106 тыс. под 8 % годовых. Сколько нужно ежегодно платить банку, чтобы рассчитаться по кредиту за три года?

3. Таксопарк вводит новый маршрут с 10 машинами на линии, стоимостью 120 тыс. за каждую. На их покупку берется кредит под 30% сложных сроком на три года. Каждая машина будет приносить в месяц 11 тыс. Сможет ли таксопарк выплатить кредит? (8% е/м. нач.).

4. Предлагается либо купить у Вас помещение за 100 тыс., либо арендовать его с правом выкупа через два года за 105 тыс. Чему должна быть равна ежемесячная арендная плата за помещение (8% ежемес. нач.)?

5. По договору Вам должны платить по 150 ежемесячно в течении первого года, по 350 ежемесячно в течении второго года и по 100 ежемесячно в течении третьего. Вам предлагают вместо этого платить по 500 ежемесячно в течении только второго года. Выгодно ли это? (8% ежемес.)

6. По договору Вам должны платить по 150 ежемесячно в течении первого года, по 350 ежемесячно в течении второго года и по 100 ежемесячно в течении третьего. Вам предлагают вместо этого платить по 500 ежемесячно в течении только второго года. Выгодно ли это? (8% е/м )

7. За три года нужно собрать 6 тыс. Сколько надо ежемесячно вносить на р/с? (8% ежемес. нач.)

8. Кредит 95 тыс. под 20 % годовых сложных с погашением в конце периода. Сколько нужно ежемесячно вносить на р/с. под 8% годовых с ежемес. начислением, чтобы рассчитаться по кредиту за два года.

9. На расчетный счет внесли 10 тыс. Сколько будет на счету через три года (8% ежемес. нач.)

10. Фирма планирует через 3 года купить оборудование за 200 000. Для этого каждый месяц фирма откладывает по 3000. К окончанию срока оборудование дорожает на 20% и в последний месяц фирма вынуждена внести недостающую сумму. Найти ее величину.

11. Некто желает приобрести ценную бумагу с ежемесячным доходом 20 в течение последующих трех лет. Какова настоящая стоимость этой ценной бумаги (8% ежемес. начисление)

12. Вы предполагаете взять кредит в 9000 на два года под 8% годовых при условии ежегодного начисления для покупки актива, который может принести за:

1-й год использования -4600:

2-й год использования - 4700

3-й год использования – 1000

Следует ли покупать актив?

13. Ежегодный платеж по аренде составляет 300.000 долл. Ставка дисконтирования равна 8%. Какова текущая стоимость платежей за три года?

14. Какую сумму следует сегодня депонировать в банке, начисляющем 8% годовых при ежемесячном накоплении, для того, чтобы через 2 года получить 10.000 долл.?

15. Какими должны быть ежегодные платежи по ипотеке в 100.000 долл. при 8% годовых? Выплата производится раз в год, срок погашения кредита 3 года.

16. Каким должен быть ежемесячный платеж в погашение 1000-долларового кредита, предоставленного под 8% годовых на два года?

17. Для оплаты за обучение ребенка (сумма составляет 20000 долл.) родители должны накопить данную сумму за 3 года. Ежегодный платеж в банк, который они могут себе позволить, составляет 5000 долл. под 8 % годовых. Смогут ли родители скопить к нужному сроку необходимую сумму (для всех вариантов исходные данные одинаковы)