МИНОБРНАУКИ РОССИИ

Государственное образовательное учреждение

высшего профессионального образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

МОРСКОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

ФИРСОВА А.В.

Учебное пособие

Санкт – Петербург

2011 год

Оглавление

Введение 2

Простая процентная ставка 3

Сложная процентная ставка 5

Учётная ставка 7

Эффективность различных ставок. Эквивалентные ставки. Эффективная ставка 8

Функции сложного процента. Техника финансовых вычислений при помощи Excel 10

Самоамортизирующийся кредит 18

Показатели оценки эффективности инвестиций 20

Введение

Деньги, денежные средства, как универсальный эквивалент материального обращения, в отличие от других универсальных человеческих ценностей, таких как красота, талант, здоровье, знания, квалификация, общение могут быть заимствованы. Заимствование – простейший вид финансовой сделки (операции) заключающийся в предоставлении некоторой суммы в долг, с условием возврата через какое-то время и, как правило, в большем объеме. Возврат денег в большем объеме, наращение суммы исходного долга к моменту возврата, обусловлено фактором неравноценности денег относительно различных моментов времени.

Временная ценность денег (от слова время, а не временно) является объективно существующей характеристикой денежных ресурсов в условиях рынка. «Время – деньги». Неравноценность денег во времени проявляется тогда, когда есть возможность их превращения в капитал, т.е. должна существовать возможность инвестиций. Иными словами – возможность изъять денежные средства из потребления и пустить их в оборот «деньги-товар-деньги», который через некоторое время вернет вложенные деньги с прибылью. Важно то, что временная ценность денег актуальна только при наличии возможности их вложения, приносящего их рост.

Таким образом, в силу различной ценности денег во времени при рассмотрении финансовых вопросов ВСЕГДА следует рассматривать величину денежных средств в привязке к моменту времени в который данная сумма средств возникает. Часто употребляют термин датированная сумма.

Наращение – процесс увеличения с течением времени значения какой-либо величины, например, задолженности или величины вклада, реализуется с учётом процентов.

Капитализация процентов — присоединение процентов к основной сумме долга.

Дисконтирование — обратно наращению, при котором сумма денег, относящаяся к будущему, уменьшается на величину соответствующую дисконту (скидке).

Процентная ставка — относительная величина дохода за фиксированный отрезок времени. Отношение дохода (процентных денег — абсолютная величина дохода от представления денег в долг) к сумме долга.

Период начисления — это временной интервал, к которому приурочена процентная ставка, его не следует путать со сроком начисления. Обычно в качестве такого периода принимаю год, полугодие, квартал, месяц, но чаще всего дело имеют с годовыми ставками.

Срок начисления – это временной интервал, от начала до конца операции над средствами.

Реальная процентная ставка определяется с учетом уровня инфляции. Она равна номинальной процентной ставке, которая устанавливается под воздействием спроса и предложения, за вычетом уровня инфляции:

r = i — %ΔP

r — реальная процентная ставка;

i — номинальная процентная ставка;

%ΔP — общий уровень цен.

Если, например, банк предоставляет кредит и взимает при этом 15%, а уровень инфляции составляет 10%, то реальная процентная ставка равна 5% (15% — 10%).

Номинальная процентная ставка – объявленная процентная ставка без поправок на инфляционную составляющую.

Простая процентная ставка

Простая процентная ставка – процентная ставка, которая применяется к одной и той же, начальной сумме на протяжении всего срока ссуды либо депозита. В таком случае база начисления – величина постоянная.

FV = PV (1+i*n), где FV – будущая стоимость

PV – настоящая стоимость

i - процентная ставка

n – количество периодов начисления (срок начисления)

Г рафик роста по простым процентам

FV FV

INT

PV

Пример:

Определить сумму накопленного долга через 2 года, если ставка по простым процентам 20% годовых , ссуда равна 150 у.е.

Решение:

FV = 150 (1+0,2*2) = 180 у.е.

Встречаются ситуации, когда срок ссуды меньше периода начисления, тогда

, где t — число дней ссуды

k — временная база начисления процентов (time basis)

Временная база может быть равна:

360 дней. В в этом случае получают обыкновенные или коммерческие проценты.

365 или 366 дней. Используется для расчета точных процентов.

Число дней ссуды. Точное число дней ссуды — определяется путем подсчета числа дней между датой ссуды и датой ее погашения. День выдачи и день погашения считаются за один день. Точное число дней между двумя датами можно определить по таблице порядковых номеров дней в году.

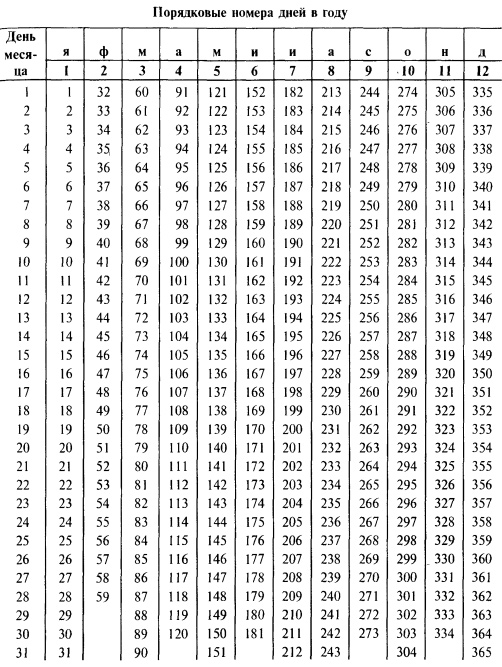
Приближенное число дней ссуды — определяется из условия, согласно которому любой месяц принимается равным 30 дням.

На практике применяются три варианта расчета простых процентов:

Точные проценты с точным числом дней ссуды (365/365)

Обыкновенные проценты с точным числом дней ссуды (банковский; 365/360). При числе дней ссуды, превышающем 360, данный способ приводит к тому, что сумма начисленных процентов будет больше, чем предусматривается годовой ставкой.

Обыкновенные проценты с приближенным числом дней ссуды (360/360). Применяется в промежуточных расчетах, так как не очень точный.

Пример:

Ссуда в размере 1 млн.рублей выдана 20 января до 5 октября включительно под 18% годовых. Какую сумму должен заплатить должник в конце срока при начислении простых процентов? Рассчитать в трех вариантах подсчета простых процентов.

Решение:

Для начала определим число дней ссуды: 20 января это 20 день в году, 5 октября — 278 день в году. 278 — 20 = 258. При приближенном подсчете — 255. 30 января — 20 января = 10. 8 месяцев умножить на 30 дней = 240. итого: 240 + 10 + 5 = 255.

1. Точные проценты с точным числом дней ссуды (365/365)

FV = 1 000 000 * (1 + (258/365)*0.18) = 1 127 233 руб.

2. Обыкновенные проценты с точным числом дней ссуды (360/365)

FV = 1 000 000 * (1 + (258/360)*0.18) = 1 129 000 руб.

3. Обыкновенные проценты с приближенным числом дней ссуды (360/360)

FV = 1 000 000 (1 + (255/360)*0.18) = 1 127 500 руб.

Задачи для самостоятельного решения:

1. 15 декабря получена ссуда 150 у.е. под 10% годовых (простых). Срок возврата – 5 января. Определить сумму погашения с учётом приближенного начисления процентов.

2. на расчетный счёт за 4 года поступило 400$. Какую сумму можно сегодня взять в кредит, если возврат будет осуществляться поступлением? 15% годовых (простых).

3. за какой срок вклад в 5000 возрастёт до 6000? Простая ставка в 32%.

4. на какой срок необходимо поместить некую сумму под 20% годовых простых, чтобы она возросла в 2,5 раза?

5. вкладчик собирается разместить в банке 1500. Какую % ставку должен обеспечить банк для того, чтобы через 3 года вклад вырос на 50%?

6. найти величину дохода кредитора, если при предоставлении некоторой суммы на 0,5 года он получил 46550 руб., 22% годовых простых.

7. на какой срок необходимо разместить сумму под 30% годовых простых, чтобы начисленные процентные платежи превысили первоначальную сумму в 1,8 раза?

8. ссуда в размере 5 млн. выдана на полгода по простой ставке ссудных процентов 20% годовых. Определить наращенную сумму.

Домашнее задание:

Придумать самостоятельно 4 задачи на нахождение переменных при условии начисления простой годовой ставки.