2. Инвариантность к возмущениям

Инвариантность к возмущениям означает способность системы компенсировать возмущения при заданной величине задания по каждому контуру.

1. ∆ = 0,25 моль/л, Процент отклонения 25%

∆( =0.352 = ∆( =0.0176

∆( =90 = ∆( =4.5

б)

а)

г)

в)

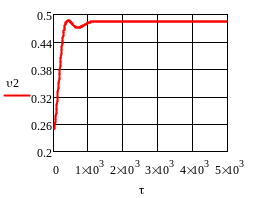
Рис.4.2.1. Изменение регулируемых переменных (Св, t) и регулирующих воздействий

при ∆ = 0,25 моль/л

а) ; б) ; в) ; г) .

б)

а)

г)

в)

Рис. 4.2.2. Изменение регулируемых переменных (Св, t) и регулирующих воздействий

при ∆ 0,25 моль/л

а) ; б) ; в) ; г) .

Анализ результатов моделирования представленных на рис. 4.2.1. и рис.4.2.2. показывает:

• Величина статической и динамической ошибки лежат в переделах допустимых значений;

• Время регулирования также удовлетворяет сформулированным требованиям;

• Значение расхода , при отрицательной подаче возмущения, оказалось отрицательным, что не имеет физического смысла и не может быть реализовано.

Следовательно, необходимо проанализировать работу системы при меньших возмущениях или наложить ограничения на регулирующие воздействия: если , то принять .

Подадим возмущение по с процентом отклонения 20%.

= 1

б)

а)

г)

в)

Рис.4.2.3. Изменение регулируемых переменных (Св, t) и регулирующих воздействий

при ∆ = 0,2 моль/л

а) ; б) ; в) ; г) .

∆( =0 = 0.01402

∆( =0 = 1.42

б)

а)

г)

в)

Рис. 4.2.4. Изменение регулируемых переменных (Св, t) и регулирующих воздействий

при ∆ 0,2 моль/л

а) ; б) ; в) ; г) .

∆( =0 = 0.01507

∆( =0 = 1.282

Анализ результатов моделирования представленных на рис. 4.2.3. - рис.4.2.4. показывают:

• Величина статической и динамической ошибки лежат в переделах допустимых значений;

• Время регулирования также удовлетворяет сформулированным требованиям;

• Значения расходов и при подаче возмущений имеют физический смысл.

2. ∆t₁= 10 , Процент отклонения 33%

∆( =0.352 = ∆( =0.0176

∆( =90 = ∆( =4.5

б)

а)

г)

в)

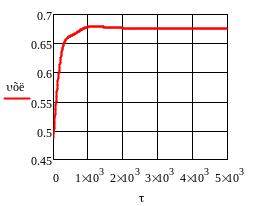
Рис.4.2.5. Изменение регулируемых переменных (Св, t) и регулирующих воздействий

при ∆t₁=10

а) ; б) ; в) ; г) .

∆( =0 = 0.00237

∆( =0 = 1.838

б)

а)

г)

в)

Рис.4.2.6. Изменение регулируемых переменных (Св, t) и регулирующих воздействий

при ∆t₁= - 10

а) ; б) ; в) ; г) .

∆( =0 = 0.00296

∆( =0 = 1.695

3. ∆t₂= 10 , Процент отклонения 25%

∆( =0.352 = ∆( =0.0176

∆( =90 = ∆( =4.5

б)

а)

г)

в)

Рис. 4.2.7. Изменение регулируемых переменных (Св, t) и регулирующих воздействий

при ∆t₂= 10

а) ; б) ; в) ; г) .

∆( =0 = 0.00062

∆( =0 = 0.69

б)

а)

г)

в)

Рис. 4.2.8. Изменение регулируемых переменных (Св, t) и регулирующих воздействий

при ∆t₂= - 10

а) ; б) ; в) ; г) .

∆( =0 = 0.00115

∆( =0 = 0.482

4. ∆ = 0 , Процент отклонения 67%

∆( =0.352 = ∆( =0.0176

∆( =90 = 1

б)

а)

г)

в)

Рис. 4.2.9. Изменение регулируемых переменных (Св, t) и регулирующих воздействий

при ∆ = 20

а) ; б) ; в) ; г) .

∆( =0 = 0.0025

∆( =0 = 2.24

б)

а)

г)

в)

Рис. 4.2.10. Изменение регулируемых переменных (Св, t) и регулирующих воздействий

при ∆ = - 20

а) ; б) ; в) ; г) .

∆( =0 = 0.00245

∆( =0 = 1.391

5. ∆ ₁ = 0,2 л/мин, Процент отклонения 27%

∆( =0.352 = ∆( =0.0176

∆( =90 = ∆( =4.5

б)

а)

г)

в)

Рис. 4.2.11. Изменение регулируемых переменных (Св, t) и регулирующих воздействий

при ∆ ₁ = 0,2 л/мин

а) ; б) ; в) ; г) .

∆( =0 = 0.00655

∆( =0 = 1.172

б)

а)

г)

в)

Рис. 4.2.12. Изменение регулируемых переменных (Св, t) и регулирующих воздействий

при ∆ ₁ = - 0,2 л/мин

а) ; б) ; в) ; г) .

∆( =0 = 0.00478

∆( =0 = 0.52

Анализ результатов моделирования представленных на рис. 4.2.5. и рис.4.2.12. показывает:

• Величина статической и динамической ошибки лежат в переделах допустимых значений;

• Время регулирования также удовлетворяет сформулированным требованиям;

• Значения расходов и при подаче возмущений имеют физический смысл.