3. Вопросы для самоконтроля

4.4.1. Определите направление действия ЭДУ на проводник с током, находящийся между полюсами 1 и 2 электромагнита. Направление токов в проводнике и в катушке электромагнита показано на рис. 43.

Рис. 43. К определению направления действия ЭДУ

4.4.2. Чем отличаются выражения для ЭДУ между параллельными проводниками бесконечной и конечной длины?

4.4.3. Как влияет форма сечения проводников на величину электродинамической силы?

4.4.4. Как рассчитываются ЭДУ в круговом витке и между витками?

4.4.6. Покажите направление магнитных силовых линий поля между полюсами (рис. 44). Сделайте обозначение полярности полюсов электромагнитов. Определите направление действия ЭДУ на проводник с током, расположенный между полюсами.

Рис. 44. К определению полярности полюсов и направления действия ЭДУ

4.4.7. Чем обусловлена сила отталкивания контактов, и к каким вредным последствиям она может привести?

4.4.8. Объясните причину возникновения электродинамической силы между проводником с током и ферромагнитным телом, и приведите пример ее использования в электрических аппаратах.

4.4.9. К

Рис. 3

ак рассчитываются ЭДУ внутри контура с током и между токоведущими контурами с помощью энергетического метода.

4.4.10. Как отреагирует деталь 3 (рис. 45), свободно лежащая на полюсах электромагнита 1, если в катушку 2 подать импульс тока путем разряда конденсатора С через замыкающий ключ К в случае, если деталь 3 выполнена: из стали, из меди, из пластмассы? Обоснуйте ответы.

Рис. 45. К определению направления действия ЭДУ на деталь

4 .4.11.Объясните суть первого метода расчета электродинамических сил (на основе закона Ампера).

4.4.12. В каком случае ЭДУ между проводниками прямоугольного сечения, обтекаемыми токами, будут больше: при взаимном расположении по рис. 46,а или по рис. 46,б? Обоснуйте ответ.

Рис. 46. К определению влияния 4.4.13. С позиции теории ЭДУ объясните

взаимного расположения принцип действия устройства, состоящего

проводников на ЭДУ из С-образного электромагнита перемен-

ного тока, между полюсами которого расположен алюминиевый диск (например: счетчик электроэнергии).

4.4.14. Что понимается под электродинамической стойкостью электрических аппаратов.

4.4.15. Как направлены ЭДУ и моменты в системах взаимно перпендикулярных проводников?

4.4.16. Приведите примеры устройств, принцип действия которых основан на взаимодействии проводника с током и ферромагнитным телом.

4.5. Примеры расчета [6]

4.5.1. Определить величину ЭДУ, возникающего между двумя расположенными параллельно друг другу шинами прямоугольного сечения h x b = 100 x 10 мм на длине l = 2 м. Расстояние между осями шин а = 20 мм, по ним протекает ток короткого замыкания I_кз = 54 кА. Шины находятся в воздухе вдали от ферромагнитных частей и ток распределен равномерно по их сечению. Шины расположены широкими сторонами друг к другу.

Решение. Величина ЭДУ определяется по формуле

.

Для данного расположения проводников величина соотношения

; .

Коэффициент формы из [6] равен k_ф = 0,44.

Тогда Н.

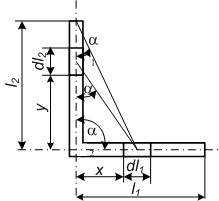
4.5.2. Определить ЭДУ, действующее на проводник 1, со стороны проводника 2 (рис. 47), если по проводникам протекает постоянный ток I = 12 кА, а длины участков l₁ = 1 м, l₂ = 2 м. Проводники круглые диаметром d = 10 мм и находятся в воздухе на достаточном удалении от ферромагнитных частей.

Рис. 47. К расчету ЭДУ Ршение. Выделим элементы проводников dl₁ dl₂ и определим элементарную силу, действующую со стороны элемента dl₂ на элемент dl₁. Так как проводники находятся в одной плоскости, то со стороны проводника 2 на проводник 1 действует элементарная сила

, (107)

или для Гн/м,

.

Суммарная сила, действующая на проводник 1,

. (108)

Здесь

; ; ; ; .

После интегрирования и, учитывая, что , получаем

Н.

4.5.3. Определить ЭДУ, действующее между параллельно расположенными шинами, если I₁ = 10 кА, I₂ =15 кА, l₁ = 1м, l₂ =1,5 м, а = 0,5 м.

Решение. ЭДУ определим по формуле

.

Коэффициент контура электродинамических усилий [6]

, (109)

для воздуха Гн/м.

Тогда, Н.

4.5.4. Определить усилие, разрывающее проводник с током I =100 кА в месте, где проводник изменяет свое поперечное сечение от D = 50 мм до d = 20 мм.

Решение. Для нахождения усилия, разрывающего проводник, воспользуемся формулой

Н.

4.5.5. На каком минимальном расстоянии можно поставить опорные изоляторы в распределительном устройстве, если в нем применены прямоугольные медные шины сечением 100 х 10 мм по одной шине на фазу. Шины закреплены жестко на опорах, поставлены на ребро и по ним протекает ток трехфазного короткого замыкания, установившееся значение которого I_уст = 507 кА. Расстояние между фазами равно 0,3 м.

Решение. Определим значение ЭДУ, действующего на 1 м длины шин, при этом расчетное значение тока определим по формуле

кА.

Здесь k_уд= 1,8.

Сила, действующая на 1 м длины

Н/м.

Для многопролетной балки [6]

, (110)

где – момент сопротивления поперечного сечения шины; Н/м – допустимое напряжение на изгиб для меди.

Подставив числовые значения, получим

,

откуда l_1мин = 0,65 м.

Поскольку по шинам протекает переменный ток, необходимо найти минимальное расстояние между изоляторами в случае отсутствия механического резонанса. При этом, собственная частота шин должна быть меньше частоты механических колебаний, т. е. двойной частоты тока: , (111)

где k = 112 для жесткого закрепления шин; E = 11,8∙10⁶ Н/см² – модуль упругости для меди; см⁴ – момент инерции сечения шины; γ = 85,2 Н/см³ – удельный вес меди; S –поперечное сечение шины.

После решения равенства (114) относительно l_2мин получаем требуемое расстояние между изоляторами

l_2мин = 0,596 м.

Выбираем наименьшее из двух полученных значений, т. е.

l_мин = 0,6 м.