Значення індексу узгодженості для випадкових матриць (математичне сподівання індексу узгодженості м(іу)

Розмір матриці	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Випадкова узгодженість	0	0	0,58	0,9	1,12	1,24	1,34	1,41	1,45	1,49	1,51	1,48	1,56	1,57	1,59

Відношення узгодженості є часткою від ділення індексу узгодженості (ІУ) на відповідне значення випадкової узгодженості

. (8)

Якщо отримане значення є меншим, ніж 10-15%, то рівень узгодженості може вважатися задовільним. У деяких випадках можна обмежитися і рівнем у 20%.

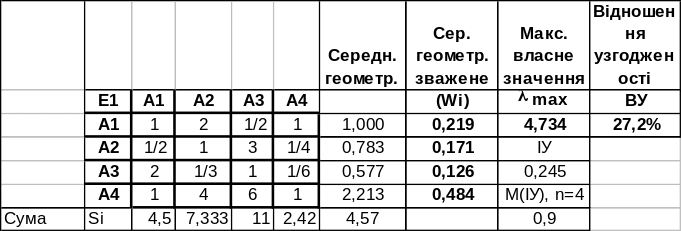
Приклад 4 .Використовуючи відношення узгодженості, перевірити матриці попарних порівнянь Прикладів 2 та 3 на порушення транзитивності.

Розв’язок:

1. Перевіримо матрицю Прикладу 2 на порушення транзитивності. Для цього спочатку знайдемо суму елементів матриці по стовпцях та обчислимо максимальне власне значення за (7): . Використовуючи (6), обчислимо індекс узгодженості: ІУ=0.122. Значення індексу узгодженості для випадкової матриці порядку n=4 (табл. 2) дорівнює 0.9. Отже , за (8) одержимо значення відношення узгодженості 13.5 %: (див. табл. Прикладу 2), яке можна вважати прийнятним.

Якщо ж взяти більш точне значення для власного значення за ітераційним алгоритмом , то одержимо ІУ=0.096 і ВУ = 10.7%.

2. Для матриці з Прикладу 3 маємо відношення узгодженості 27.5%, що є неприйнятним і тому треба переглянути матрицю попарних порівнянь.

Методи знаходження найбільш неузгоджених експертних оцінок, що призводять до порушення їх транзитивності

Найбільш неузгоджені експертні оцінки, що призводять до нетранзитивних ранжувань називають викидами. Викиди здебільшого виникають внаслідок неточного вводу чи випадкових помилок  однією з причин появи викидів може бути неправильне розміщення отриманих від експерта оцінок в симетричні позиції матриць парних порівнянь. Існує декілька методів знаходження викидів у матриці попарних порівнянь.

Метод послідовного виключення альтернатив. Один із методів базується на обчисленні індексу узгодженості ІУ для n укорочених матриць попарних порівнянь (матриць порядку n-1) , отриманих з початкової (порядку n) послідовним виключенням однієї з альтернатив (у вихідній матриці  послідовним виключенням відповідного рядка та стовпця). Якщо при вилученні і-ї альтернативи ІУ (тобто з початкової матриці вилучається і-тий рядок та і-тий стовпець) є найменшим серед усіх інших n-1 скорочених матриць, то це свідчить про те, що аномальна оцінка (викид), яка призводить до неузгодженості вихідної матриці та порушення її транзитивності знаходиться у і-му рядку (та на симетричній позиції у j-му стовпці). Тому, якщо два найменші значення ІУ для скорочених матриць досягаються при вилученні і-ї та j-ої альтернативи, то найбільш аномальною буде оцінка (та відповідно симетрична оцінка ), яку треба переглянути.

Приклад 5.

Перевірити матрицю на порушення транзитивності за допомогою ВУ та визначити аномальні оцінки у матриці (викиди) методом послідовного виключення альтернатив.

Розв’язок:

1. Знайдемо ІУ та ВУ:

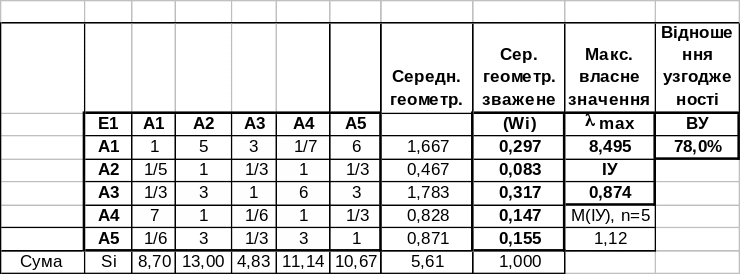
Отже, ВУ=78%, що свідчить про суттєве порушення транзитивності.

2. Розглянемо укорочену матицю, яка одержується з вихідної вилученням 1-ї альтернативи (1-го рядка та 1-го стовпця):

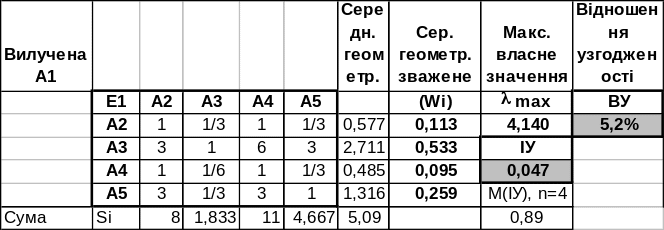
Далі, розрахуємо ІУ для укороченої матриці після вилучення А2:

Аналогічно розраховуються ІУ при послідовному вилученні А3, А4, А5. Результати наведено у таблиці:

Отже, найменші значення ІУ набуває при вилученні 1-ї, та 4-ї альтернативи, тому необхідно переглянути оцінку (та відповідно симетричну ). Якщо взяти , одержимо, що ІУ=7,5% .

Метод розрахунку кореляції між рядками та стовпчиками.

Цей метод ґрунтується на тому, що зі збільшенням узгодженості матриці кореляція між рядками (та стовпцями) прямує до одиниці. Метод складається з наступних кроків:

Розраховуються математичні сподівання коефіцієнтів кореляції між і-тим та усіма іншими рядками та знаходиться . Аналогічно розраховуються математичні сподівання коефіцієнтів кореляції між j-тим та усіма іншими стовпцями та знаходиться . Якщо ці мінімуми досягаються у рядку з номером та стовпцю з номером , то елемент буде аномальним (викидом).

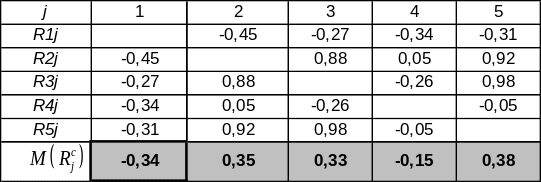
Приклад 6.

Застосуємо цей метод для умови прикладу 5. У стовпці знаходяться коефіцієнти кореляції 1-го рядка з усіма іншими, в останньому  математичні сподівання коефіцієнтів кореляції між і-тим та усіма іншими рядками.

У рядку знаходяться коефіцієнти кореляції 1-го стовпця з усіма іншими, в останньому  математичні сподівання коефіцієнтів кореляції між j-тим та усіма іншими стовпцями.