3 Этап. Решение задачи инструментом Поиск решения.

Для решения моего примера инструментом Поиск решения в диалоговом окне Поиск решения, показанном на рис.2 делаю щелчок по кнопке Выполнить. В этом окне ставлю флажок на опцию Сохранить найденное решение и затем щелкаю на кнопке ОК. На рис.5. изображены вышеперечисленные действия.

Рис.5. Диалоговое окно Результаты поиска решения

Результат решения моего примера приведен на рис.6.

Рис.6. Результат решения примера линейной производственной задачи

Здесь значения компонент вектора x содержатся в ячейках диапазона C8:F8. Значение максимальной прибыли – в ячейке H4. А значения расходов всех используемых ресурсов содержатся в ячейках диапазона H5:H7.

4 Этап. Анализ полученного решения.

Из результатов решения линейной производственной задачи, приведенных на рис.6, видно, что в оптимальной производственной программе, что 4-й продукт выпускается в количестве 37 единиц. А 1-й,2-й 3-й продукт не выпускаются. Объемы всех ресурсов использованы не полностью. Максимальная прибыль равна 1073 денежных единиц.

Для получения дополнительной информации о полученном решении я сделала 3 отчета, которые я создала с помощью инструмента Поиск решения. Для этого после окончания его работы в диалоговом окне Результаты поиска решения, выделяю нужные отчеты и ставлю флажок на опцию Восстановить исходные значения и затем щелкаю кнопку ОК. На рис. 7 изображены вышеперечисленные действия.

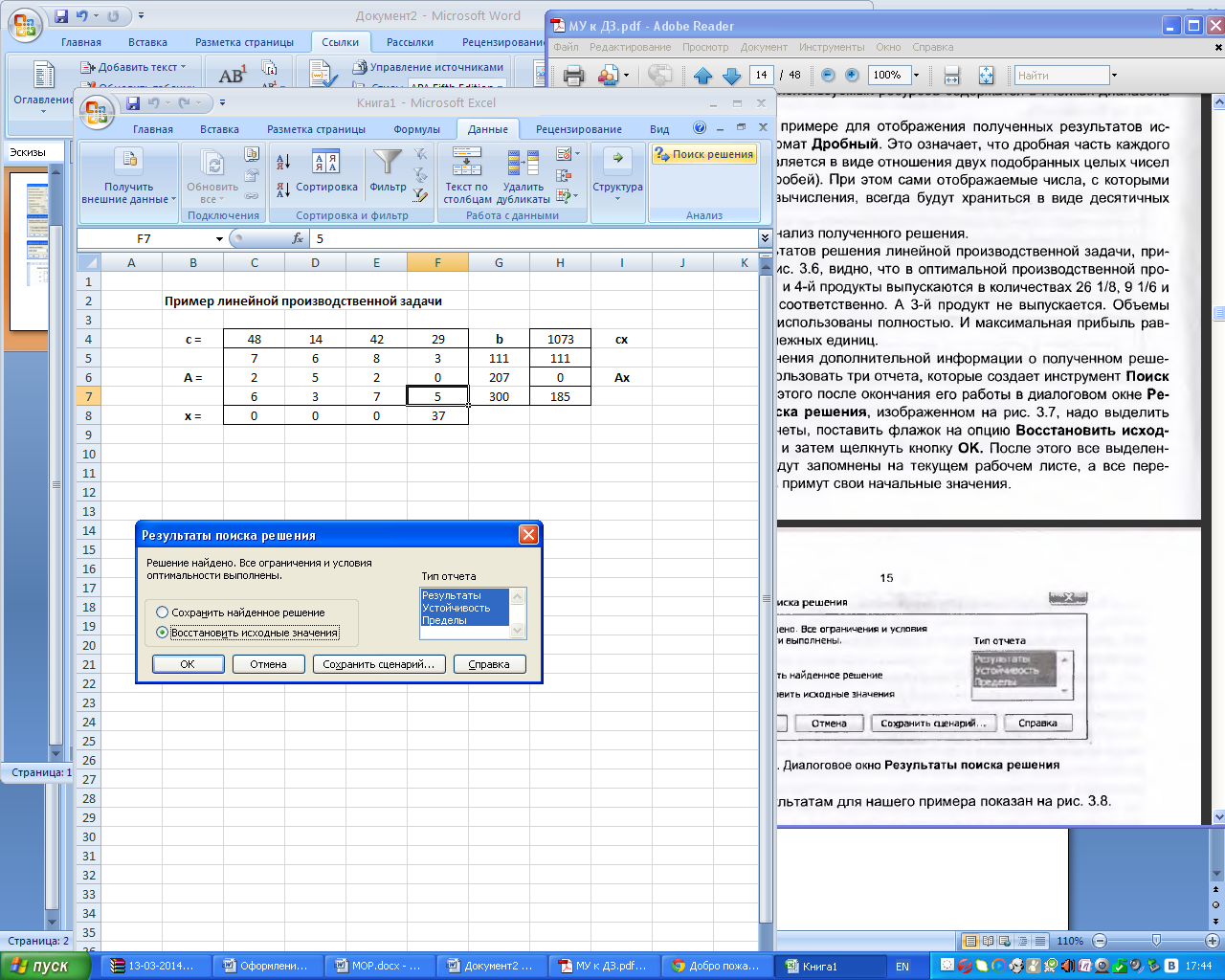
Рис.7. Диалоговое окно Результаты поиска решения

Отчет по результатам для моего примера показан на рис.8.

Рис.8. Отчет по результатам

для примера линейной производственной задачи

В первой таблице Целевая ячейка этого отчета дана ссылка на ячейку, содержащую значение целевой функции. Указано также то, что это значение максимизируется, приведены его начальное и конечное значения.

Во второй таблице Изменяемые ячейки отчета по результатам показаны ссылки на ячейки, содержащие значения переменных задачи, указаны их начальные и конечные значения.

В третьей таблице Ограничения этого отчета приведены ограничения

задачи, указанные в диалоговом окне Поиск решения на рис.2. В ней показаны также конечные значения ячеек диапазона Н5:Н7, содержащие переменные значения левых частей неравенств задачи. Статус связанное означает, что соответствующее неравенство для оптимального решения выполняется как равенство. А статус не связан означает, что это неравенство для оптимального решения выполняется как строгое неравенство. В последнем столбце третьей таблицы стоят разности между правыми и конечными значениями левых частей ограничений задачи.

Отчет по устойчивости для моего примера показан на рис.9.

Рис.9. Отчет по устойчивости

для примера линейной производственной задачи

Наибольший интерес в нем представляет числа 9,666666667; 0; 0 стоящие в четвертом столбце Теневая Цена второй таблицы Ограничения. Они являются компонентами оптимального решения задачи линейного программирования. По первой теореме двойственности сумма их произведений на соответствующие элементы пятого столбца Ограничение Правая часть той же таблицы равна оптимальному значению (значению максимальной прибыли) линейной производственной задачи.

Отчет по пределам для моего примера показан на рис.10.

Рис.10. Отчет по пределам

для примера линейной производственной задачи

В нем указаны значения нижних и верхних границ для каждой из переменных

задачи. При этом значения всех других переменных должны быть фиксированы. А набор значений всех переменных должен удовлетворять каждому из ограничений задачи. В отчете по пределам также приведены значения целевой функции для случаев, когда значение соответствующей переменной равно его нижней или верхней границе.