
- •Задача 1. Линейная производственная задача
- •Решение задачи с помощью симплекс - метода.
- •Решение задачи с помощью инструмента «Поиск решения» программного продукта Microsoft Excel.
- •1 Этап. Ввод исходных данных оптимизации.
- •2 Этап. Вызов инструмента Поиск решения и ввод условий задачи.
- •3 Этап. Решение задачи инструментом Поиск решения.
- •4 Этап. Анализ полученного решения.
- •Сравнение полученных результатов
Министерство образования и науки Российской Федерации
(МИНОБРНАУКИ РОССИИ)
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УПРАВЛЕНИЯ»
Институт информационных систем управления
Кафедра математических методов в управлении
по дисциплине: «Методы оптимальных решений»
ДОМАШНЯЯ РАБОТА №1
на тему: «Линейное программирование»
Выполнил(а) студент(ка) очной формы обучения Сергиенко А.В. 2 курса 3 группы
|
____________________ (подпись) |
__________________________ (инициалы, фамилия) |
Принял |
____________________ (подпись) |
Е.Ю. Луценко |
Москва 2014 год
Вариант 20.
Задача 1. Линейная производственная задача
Решение задачи с помощью симплекс - метода.
Составить производственную программу, обеспечивающую предприятию наибольшую прибыль при имеющихся ограниченных ресурсах.
Таблица 1. Исходные данные
c = |
48 |
14 |
42 |
29 |
b |
|
7 |
6 |
8 |
3 |
111 |
A = |
2 |
5 |
2 |
0 |
207 |
|
6 |
3 |
7 |
5 |
300 |
В верхней строке записаны компоненты вектора удельных прибылей c.
Под компонентами вектора с стоят элементы матрицы удельных затрат ресурсов А.
В крайнем правом столбце записаны компоненты вектора объемов ресурсов b.
Пусть
 -
это количество единиц j-гo
продукта, выпускаемого в течение
-
это количество единиц j-гo
продукта, выпускаемого в течение
дня, j = 1,2,3,4. Все количества выпускаемых продуктов - неотрицательны.
В матричном виде:
 ,
,

Математическая модель задачи
найти производственную программу

максимизирующую прибыль

при ограничениях по ресурсам

Таблица 2. Симплекс-таблица
|
Б |
H |
48 14 42 29 0 0 0 |
|
Примечание |
||||||||
|
|
|
|
|
|
|
|
|
|||||
0 |
|
111 |
7 |
6 |
8 |
3 |
1 |
0 |
0 |
111/7 |
min(P < 0) = - 48 в базис min
( |
||
0 |
|
207 |
2 |
5 |
2 |
0 |
0 |
1 |
0 |
207/2 |
|||
0 |
|
300 |
6 |
3 |
7 |
5 |
0 |
0 |
1 |
300/6 |
|||
|
P |
0 |
-48 |
-14 |
-42 |
-29 |
0 |
0 |
0 |
|
|||
48 |
|
111/7 |
1 |
6/7 |
8/7 |
3/7 |
1/7 |
0 |
0 |
37 |
min(P
< 0) =
в базис min
(
|
||
0 |
|
1227/7 |
0 |
23/7 |
-2/7 |
-6/7 |
-2/7 |
1 |
0 |
- |
|||
0 |
|
1434/7 |
0 |
-15/7 |
1/7 |
17/7 |
-6/7 |
0 |
1 |
1434/17 |
|||
|
P |
5328/7 |
0 |
190/7 |
90/7 |
-59/7 |
48/7 |
0 |
0 |
|
|||
29 |
|
37 |
7/3 |
2 |
8/3 |
1 |
1/3 |
0 |
0 |
- |
|
0 |
|
207 |
2 |
5 |
2 |
0 |
0 |
1 |
0 |
- |
|
0 |
|
115 |
-17/3 |
-7 |
-19/3 |
0 |
-5/3 |
0 |
1 |
- |
|
|
P |
1073 |
59/3 |
44 |
106/3 |
0 |
29/3 |
0 |
0 |
|
Итак,
 ,
,
т.е. определяют производственную программу

и остатки ресурсов:
первого
вида

второго
вида

третьего
вида

Из последнего уравнения системы находим P:
 ,
,
то становится очевидным, что прибыль будет наибольшей тогда, когда
,

Итак, X опт = (0,0,0,37 (0, 207, 115)) и .










 ;
; ;
; )=
)=
 из базиса
из базиса
 ;
;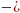 ;
; )=
)=
 из базиса
из базиса
