2.1 Методика побудови математичної моделі гідравлічного об'єкта

Задачі такого типу виникають при проектуванні автоматичних систем керування рівнями рідини . Як правило , рівень рідин регулюють або в відкритих, або в закритих ємностях та резервуарах . В першому випадку говорять про посудини з відкритою поверхнею , а в другому – про посудини , які знаходяться під тиском .

Розглянемо об'єкт (рис.2.1) , який складається із двох ємностей з'єднаних послідовно . Ємність 1 знаходиться під тиском Р₀ , а ємність 2 з відкритою поверхнею . В ємності 1 і 2 поступає рідина з відомими витратами Q₁ i Q₂ . Тиск на вході першої ємності Р₁ , а в другій ємності рідина вільно витікає . Регульованими величинами в першій і другій ємностях є рівні Н₁ і Н₂ , зміна яких досягається за допомогою витрат Q₁ i Q₂ .

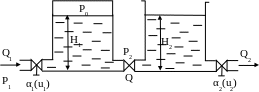
Рисунок 2.1 – Схема гідравлічного об’єкту

До складання математичної моделі приймемо такі допущення :

1. ємності 1 і 2 мають постійне поперечний переріз за висотою ;

2. газ , який знаходиться над рідиною ідеальний і його температура не змінюється :

3. тиск на вході в ємність 1 – постійний ;

4. коефіцієнт місцевого опору – постійний .

Основними фізичними законами , які притаманні процесу , що розглядаються, будуть – закон матеріального балансу та закон Бойля – Маріотта .

Рівняння матеріального балансу може бути подане в такій формі :

(швидкість накопичення рідини)=(приплив)-(стік) (2.2)

Для ідеального газу зв'язок між тиском та його об'ємом виражається формулою

V_ГP₀=MRT_Г, (2.3)

де Р₀ – тиск газу ; V_Г – об'єм газу ; T_Г – температура газу в К ; М – кількість молей газу ; R – газова стала .

Задачею регулювання являється стабілізація рівня Н₁ і Н₂ , яка здійснюється за допомогою зміни степені відкриття клапана 3 і шляхом зміни витрати Q₂ . Отже, вихідними величинами являються величини Н₁ і Н₂ , а вхідними – U₁ і Q₂ .

Складемо рівняння матеріального балансу для ємності 1 . Швидкість накопичення рідини – це зміна об'єму рідини в часі , тобто dV/dt . Оскільки площа поперечного перерізу ємності 1 постійна і дорівнює S₁ , а рівень рідини – Н₁ , то об'єм рідини буде рівний S₁ Н₁ . Тоді dV/dt можна представити як

d(S₁ Н₁)/dt , або при S₁=const dV/dt=S₁dH₁/dt. Тепер можна записати для ємності 1 рівняння

, (2.4)

де Q₁ i Q – об'ємні витрати .

Припустимо , що розширення і стиснення газу відбувається ізотермічно , тобто температура Т_г залишається постійною , а також , що випаровування з поверхні незначне . Нехай загальний об'єм ємності 1 дорівнює V ₀ . Тоді об'єм газу визначимо як V_Г=V₀ - S₁ Н₁ . Підставляючи значення V_Г в рівняння (2.3) , отримуємо

звідси

. (2.5)

Потік Q₁ (рис.2.1) іде через встановлений на вході вентиль 3 під тиском Р₁ . Тиск після вхідного вентиля дорівнює Р₂ і залежить від рівня Н₁ і тиску Р₀ . Відібраний потік Q проходить через встановлений на з'єднувальному трубопроводі вентиль , тиск після якого обумовлений рівнем Н₂ в ємності 2 .

Таким чином , витрати через вентилі 3 і 4 визначаються із рівнянь :

,

,

де  - густина рідини .

Якщо врахувати значення Р₀ , яке визначається рівнянням (2.5) , то

, (2.6)

. (2.7)

З врахуванням одержаних рівнянь (2.6) , (2.7) рівняння (2.4) прийме такий вигляд

.

(2.8)

Запишемо тепер рівняння матеріального балансу для ємності 2 . Потоки Q₁ і Q₂ вливаються в ємність , а потік Q₂ витікає із неї . Тому

. (2.9)

Величина Q визначається із рівняння (2.7) , а потік Q₂ вільно витікає із ємності 2 . Отже

, (2.10)

де ₂ – коефіцієнт витрати , який залежить від геометричних розмірів отвору і режиму витікання рідини .

Якщо врахувати рівняння (2.7) і (2.10) , то змінна рівняння Н₂ в ємності 2 буде описуватись таким диференціальним рівнянням :

.(2.11)

Таким чином , рівняння (2.8) і (2.11) утворюють математичну модель КО .