2. Определение термодинамической возможности самопроизвольного протекания химической реакции в стандартных условиях

Термодинамика устанавливает, что для любых систем, существует некоторый критерий, определяющий возможность и направление самопроизвольных процессов и момент установления равновесия. Такими критериями являются характеристические функции.

Для изолированных систем такой функцией является энтропия S.

В химической технологии изолированные системы практически не встречаются. Часто процесс приводят при постоянстве объема и температуры (в изохорно-изотермических условиях) или при постоянном давлении и постоянной температуре (в изобарно-изотермических условиях). Характеристическими функциями в этом случае являются энергия Гельмгольца и энергия Гиббса. Убыль ∆F (или∆G) характеризует при этих условиях способность системы совершать полезную работу. По мере протекания процесса и приближения системы к состоянию равновесия ее «работоспособность» уменьшается.

Таким образом, мы имеем несколько критериев возможности самопроизвольного протекания процесса (табл.).

Критерии возможности самопроизвольного протекания процесса

Функция	S	F	G
Определение		F = U-TS	G = H-TS
Чем измеряется изменение функции		l)-∆F = Amax 2) ∆F=∆U-T∆S	l)- ∆G = A´max 2) ∆G = ∆H-T∆S
Ограничения	изолированная система	T=const V = const	T = const p = const
Критерий воз­можности само­произвольного процесса	∆S>0	∆F < 0	∆G < 0
Условия равновесия	максимум S dS = 0	минимум F dF = 0	минимум G dG = 0

2. Константа равновесия химической реакции и способы выражения константы равновесия

Состояние системы, которое не изменяется во времени и ничем не поддерживается, называется равновесным.

При протекании химических реакций при определенных внешних уловиях наступает такой момент, когда число молекул веществ, составлящих систему, перестает изменяться и остается постоянным при неизменных внешних условиях. Такое состояние называется химическим равновесием.

Рассмотрим при заданных условиях какую-либо систему, в которой происходят как прямая, так и обратная реакции, где скорость прямой peaкции равна скорости обратной (W_пр = W_обр):

аА + вВ ↔ dD + rR

Пусть все участвующие в реакции вещества находятся в газообразном состоянии, каждое из которых характеризуется своим равновесным давлением р_А, р_В, p_D, р_R. В условиях равновесия dG = 0, тогда для полного дифференциала энергии Гиббса имеем

При Т= const и р = const

Подставим значения химических потенциалов веществ, образующих в систему, в последнее уравнение:

dμ_D + rμ_R – aμ_A – bμ_B =0

Учитывая, что μ_i = μ_i ° + RTlnp, подставляем значения химических потенциалов всех реагирующих веществ в последнее уравнение, отсюда

сгруппировав члены равенства, имеем

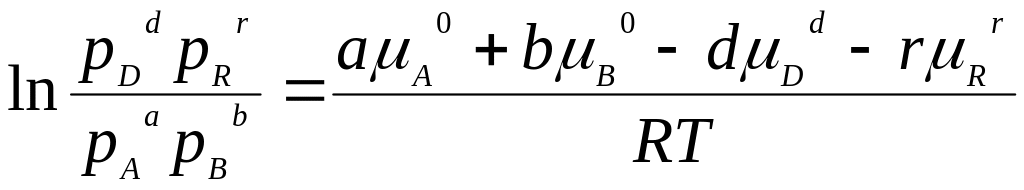
В правой части этого уравнения стоит величина, зависящая только от температуры и давления. Поскольку процесс идет в изобарно-изотермических условиях, эта величина будет постоянной. Обозначим ee lnК_р,, тогда

→

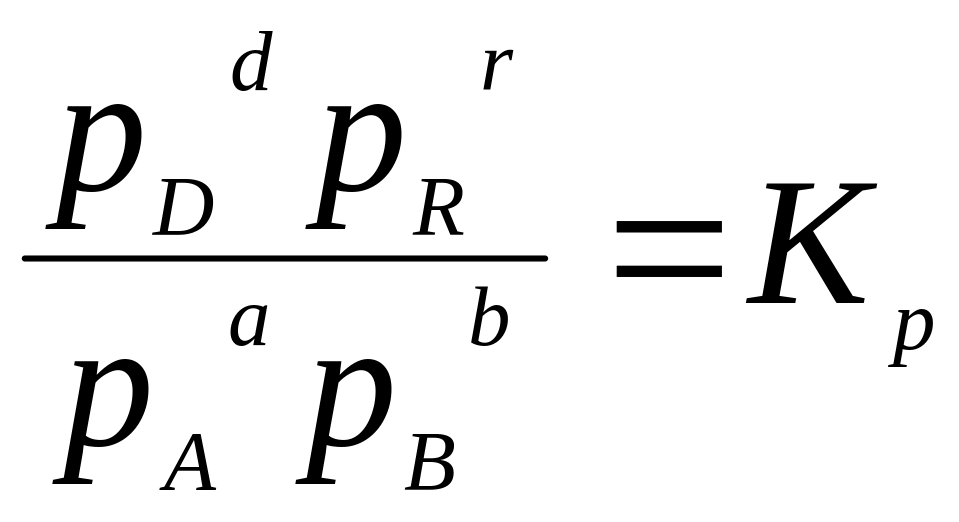
где К_р - константой равновесия химической реакции протекающей между газообразными веществами.

Если химический потенциал выразить через концентрацию

μ_i = μ_i⁰ + RTlnс_i, то, проделав аналогичные операции, получим

Константы К_р, и К_c определяют выход химической реакции. Под выходом понимают долю исходного вещества, превратившегося в конечный продукт. Если К_р >>1 или К_c >>1, то в данной системе велик выход продуктов реакции.

Уравнения для К_р и К_c называют законом действующих масс (ЗДМ), выведенным на основе термодинамики. Для газов из уравнения Менделеева-Клапейрона:

p_iV_i= n_iRT; p_i(n_i/V_i)RT=c_iRT.

Подставив последнее выражение в уравнение ЗДМ для К_р, получим уравнение взаимосвязи К_р и К_c

K_p=K_c(RT)^∆n,

где ∆n – изменение количества вещества (в моль) в реакции.

При ∆n = 0

H₂ +Cl₂ ↔ 2HCl, К_р=К_c или

При ∆n < 0

2СО + О₂↔2СО₂, К_р< К_с или <

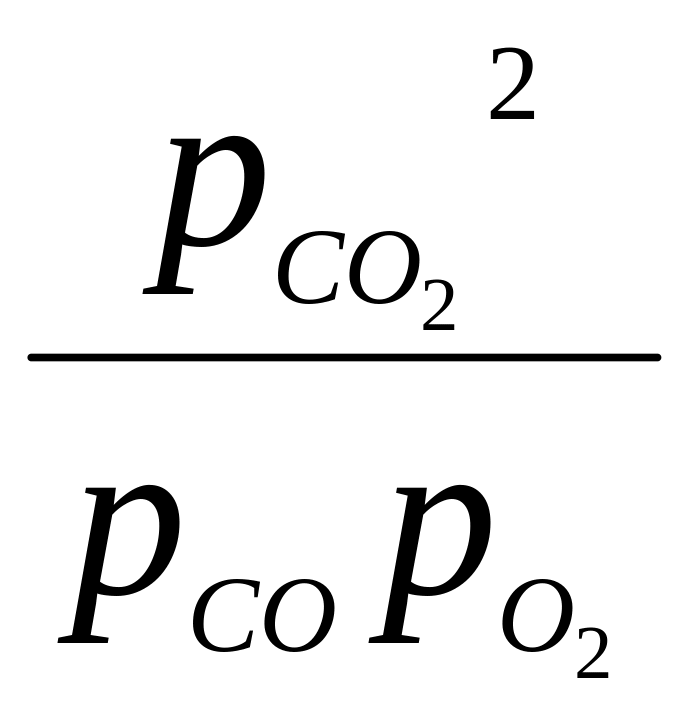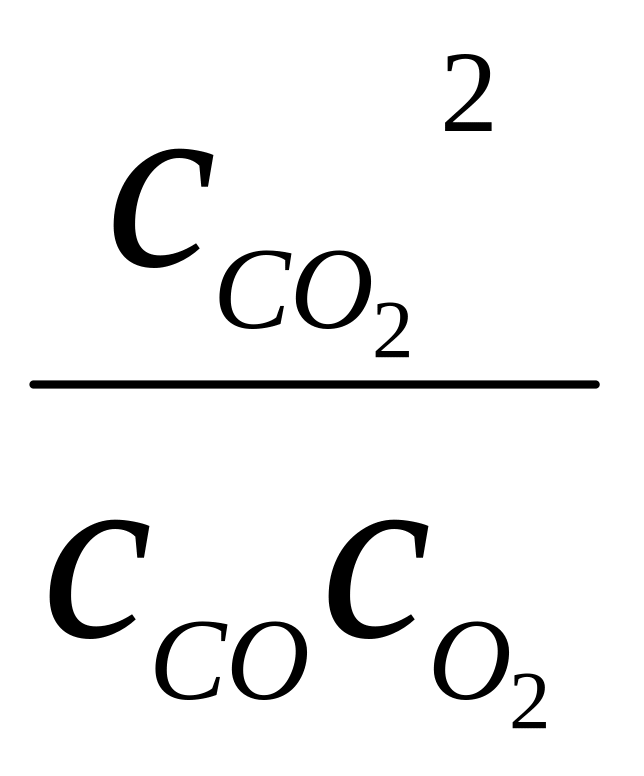
При ∆n >0

2NH₃ ↔ 3Н₂ + N₂, K_p > К_с или <

Для реальных растворов используют константу равновесия K_a, рассчитываемую через активности:

Активность а – это концентрация реального раствора, которая учитывает размеры и взаимодействия частиц реагирующих веществ.

,

где - коэффициент активности. Значение для разных веществ при разных концентрациях их растворов приведены в аналитических и физико-химических справочниках.

Для учёта взаимодействия частиц реального газа используют коэффициент фугетивности φ, а вместо давлений величину фугетивности f = φp.

Поэтому равновесие в реальных газах характеризует константой .

.

Приведенные уравнения для расчета К_р, К_c, К_N, К_a и К_f справедливы для гомогенных систем.

При выводе ЗДМ мы рассматривали гомогенные системы, в которых все компоненты находятся в газообразном состояние или в растворе. Реакции, в которых реагенты находятся в разных фазах называются гетерогенными. Ограничимся рассмотрением наиболее простых гетерогенных равновесий, в которых каждое вещество содержится системе в виде самостоятельной фазы, т.е. не образует жидких или твердь растворов.

Пусть в реакции аА + bВ = dD + rR вещество D находится в кристаллическом состоянии, тогда аналогично предыдущему получим:

где р_D — давление насыщенного компонента D, являющееся постоянно величиной.

Включая р_D в константу К_р, получаем