1 Этап. Прямой ход.
.
В квадратик возле 0 записываем 0.
Рассматриваем событие 1, в которое входит работа (0;1).
По
формуле (31):
.
Это число записываем в квадратик события
1.
Событие 2, в него входит работа (0;2):
.
Это число записываем в квадратик события
2.
Событие 3, в него входят две работы (1;3) и (2;3):
.
Это число записываем в квадратик события 3.
Событие 4, в него входят две работы (2;4) и (3;4):
.
Событие 5, в него входят работы (3;5) и (4;5):
Событие 6, в него входят две работы (3;6), (5;6) и (4;6):
2 Этап. Обратный ход.
Так как
,
то в треугольник события 6 записываем число 19.
=19,
значит,
.
Рассматриваем
предшествующее событие 5, из которого
выходит только одна работа (5;6).
Следовательно, по формуле 32 вычисляем
.
Этот результат записываем в треугольник
события 5.
Из события 4 выходят 2 работы (4;5) и (4;6). Поэтому по формуле 32:
.
Из события 3 выходят 3 работы (3;4), (3;5) и (3;6):
Из события 2 выходят 2 работы (2;4) и (2;3):
.
Из события 1 выходит работа (1;3):
Из события 0 выходят 2 работы (0;1) и (0;2):
.
Полученные данные отобразим на рисунке 4.
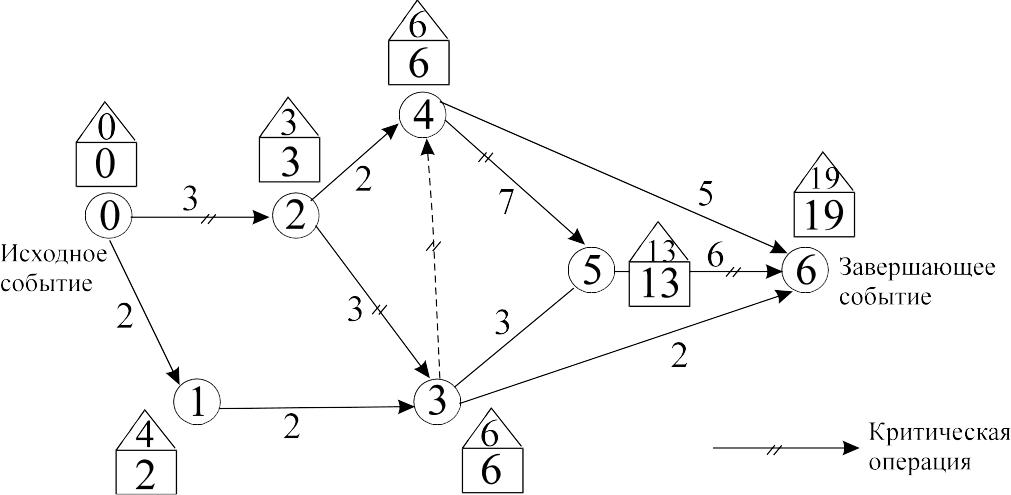
Рис. 4 Расчет сетевой модели
3 Этап. Определения резервов времени событий.
Для
определения резервов времени событий
достаточно
из чисел, записанных в соответствующих
квадратах, вычесть числа, записанные в
соответствующих треугольниках.
,
,
,
,
,
,
.
У критических событий резервы времени равны 0. В нашей задаче критическими являются события 0; 2; 3; 4; 5 и 6. Они и определяют критические работы (0;2), (2;3), (3;4), (4;5), (5;6) и критический путь 0-2-3-4-5-6. Критический путь на графе обозначим двойными дугами (рис. 4). В рассмотренной задаче критический путь на сети оказался единственным. Их может быть и несколько. Заметим еще, что данный критический путь включает и фиктивную работу (3;4).
4 Этап. Определения резервов времени работ.
Исходные данные модели поместим в ст.1 и 2 таблицы 4.1. Начинаем вычисление с показателей раннего начала работ по формуле 33 (ст.3 табл. 4.1). После чего определяем ранний срок окончания работ (ст. 4 табл. 4.1) по формуле 34. Далее определим поздний срок окончания работ (ст. 6 табл. 4 1), что поможет нам определить поздний срок начала работы (ст. 5 табл. 4.1).
После проведенных расчетов можно определить резервы времени: полный резерв времени заданной работы (ст. 7 табл. 4.1) по формуле 37 и свободный резерв времени (ст.8 табл. 4.1) по формуле 38.
Вывод. Из полученных данных можно сделать вывод, что минимальный срок всего комплекса работ составляет 19 дней. Критическими работами являются (0;2), (2;3), (3;4), (4;5), (5;6). Для этих работ необходимо установить строгий контроль за сроком выполнения. Если же длительность выполнения любой из работ критического пути увеличить, то общий срок выполнения неизбежно возрастет. Из таблицы 4.1 видно, что некоторые работы имеют резерв времени её выполнения. В пределах имеющихся резервов времени с выполнением этих работ можно не спешить, и общий срок выполнения комплекса работ не увеличиться.
Таблица 4.1
Временные параметры работ
Работа (i, j)
|
tij |
Раннее |
Позднее |
Полный резерв Rп |
Свободный резерв Rс |
||
начало tpн |
окончание tр о |
начало tп н |
окончание tпо |
||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
(0, 1) |
2 |
0 |
2 |
2 |
4 |
2 |
0 |
(0, 2) |
3 |
0 |
3 |
0 |
3 |
0* |
0 |
(1, 3) |
2 |
2 |
4 |
4 |
6 |
2 |
2 |
(2, 3) |
3 |
3 |
6 |
3 |
6 |
0* |
0 |
(2, 4) |
2 |
3 |
6 |
4 |
6 |
1 |
1 |
(3, 4) |
0 |
6 |
6 |
6 |
6 |
0* |
0 |
(3, 5) |
3 |
6 |
9 |
10 |
13 |
4 |
4 |
(3, 6) |
2 |
6 |
8 |
17 |
19 |
11 |
11 |
(4, 5) |
7 |
6 |
13 |
6 |
13 |
0* |
0 |
(4, 6) |
5 |
6 |
11 |
14 |
19 |
8 |
8 |
(5, 6) |
6 |
13 |
19 |
13 |
19 |
0* |
0 |