Раздел 4. Сетевое моделирование Тема 7. Построение сетевой модели

Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ, заданного в специфической форме сети, графическое изображение которой называется сетевым графиком. Сетевой график ­ - это связный орграф без петель и контуров. Он должен иметь только одно исходное событие - начало комплекса работ; и только одно завершающее событие - окончание всех работ комплекса. Событие – это момент заверения какого-либо процесса, отражающий отдельный этап выполнения проекта. Событие имеет двойственный характер: для всех непосредственно предшествующих ему работ оно является конечным, а для всех непосредственно следующих за ним – начальным. Событие не имеет продолжительности и совершается мгновенно. Работа – это любые целенаправленные действия, трудовые процессы, сопровождающиеся затратами ресурсов и времени и приводящие к определенным результатам (событиям). Работы на сети изображаются направленными отрезками произвольной длины (стрелками), а события кружками, в которых указывают порядковый номер или шифр события. У каждой стрелки проставляется время выполнения работы, а иногда и другие числовые характеристики (расход ресурса; количество исполнителей и др.)

Правила построения сетевой модели:

1. В сетевой модели не должно быть «тупиковых» событий, т.е. событии, из которых не выходит ни одна работа, за исключением завершающего события.

2. В сетевом графике не должно быть «хвостовых» (кроме исходного) событий, которым не предшествует хотя бы одна работа.

3. В сети не должно быть замкнутых контуров и петель, т.е. путей, соединяющих некоторые события с ними же самими.

4. Любые два события должны быть непосредственно связанны не более чем одной работой-стрелкой.

При включении каждой операции в сетевую модель для обеспечения правильного упорядочения необходимо дать ответы на следующие вопросы:

а) какие операции необходимо завершить непосредственно перед началом рассматриваемой операции?

б) какие операции должны непосредственно следовать после завершения данной операции?

в) какие операции могут выполняться одновременно с рассматриваемой.

Путь - это любая последовательность работ в сети, в которой конечное событие каждой работы этой последовательности совпадает с начальным событием следующей за ней работы. Путь от исходного до завершающего события называется полным. Продолжительность пути определяется суммой продолжительностей составляющих его работ. Полный путь, имеющий максимальную длину, называют критическим. Критический путь определяет минимальное время выполнения всех работ данного комплекса. Это максимальное среди всех полных путей время называют критическим сроком . Критическими называют события и работы, расположенные на критическом пути.

Пример 8. На рис. 3 задан сетевой граф – сеть некоторого комплекса работ. Известна продолжительность каждой работы, например в днях, которая проставлена на дуге. Требуется определить критические события, критические работы, критические пути.

Решение.

1. Рассмотрим все полные пути на сети от истока– событие 0 до стока – событие 6. Таких путей будет 10:

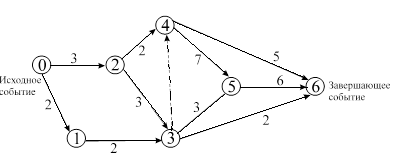
Рис. 3. Сетевая модель

2. Определим продолжительность этих путей:

(дней),

(дней),

(дней),

(дней),

(дней),

(дней),

(дней),

(дней),

(дней),

(дней).

3. Наиболее продолжительным оказался путь дней. Он является критическим. Критический путь определяет минимальное время выполнения всех работ данного комплекса. В нашем примере =19.

4. Критические события 0, 2, ,3, 4, 5, 6; критические работы: (0;2), (2;3), (3;4), (4;5), (5;6). Остальные события и работы – некритические.

Если выполнение какой-либо критической работы будет задержано, это вызовет задержку выполнения всего комплекса на тот же срок. Чтобы ускорить выполнение комплекса, необходимо сократить сроки выполнения критических работ.

Некритические работы допускают некоторое запаздывание их выполнения без нарушения критического срока.

Чтобы определить время, на которое можно задержать выполнение некритических работ, вводят понятие резервов времени событий и работ, которые в свою очередь выражаются через ранние и поздние сроки свершения событий.

Под свершением события понимается момент, к которому заканчиваются все входящие в него работы, и может быть начата любая выходящая работа.

Расчет сетевой модели включает два этапа:

1 этап. Прямой ход. Вычисления начинаются с исходного события и продолжаются до тех пор, пока не будет достигнуто завершающее событие всей сети. Для каждого события вычисляется ранний срок его наступления.

, (31)

где – множество работ, входящих в -ое событие.

2 этап. Обратный ход. Вычисления начинаются с завершающегося события сети и продолжаются, пока не будет достигнуто исходное событие. Для каждого события вычисляется поздний срок его наступления.

, (32)

где – множество работ, выходящих из -го события.

Определение критического пути: Работа (i, j) принадлежит критическому пути, если она удовлетворяет трем условиям:

1. t_п(i) = t_p(i);

2. t_п(j) = t_p(j);

3. t_р(j) - t_p(i) = t_п(j) - t_п(i) = t_ij.

Эти условия означают, что между ранним сроком и поздним сроком запас времени отсутствует. Т.е. критический путь определяет кратчайшую возможную продолжительность всей программы в целом.

Зная сроки свершения событий для работы (i; j), можно вычислить временные параметры работ:

1. Ранний срок начала работы . (33)

2. Ранний срок окончания работы . (34)

3. Поздний срок окончания работы . (35)

4. Поздний срок начала работы (36)

5. Полный резерв времени заданной работы - это максимальное количество времени, на которое можно задержать начало работы или увеличить ее продолжительность, не нарушая критический срок выполнения всего комплекса работ:

. (37)

6. Свободный резерв времени работы – это запас времени, на который можно отсрочить начало работы или увеличить ее продолжительность при условии, что она начнется в свой ранний срок, и при этом ранние сроки начала последующих работ не изменятся, а потому комплекс всех работ завершится в критический срок.

Свободный резерв времени определяется в предположении, что все операции в сети начинаются в ранние сроки. Тогда величина R_с(i, j) для операции (i, j) представляет собой превышение допустимого отрезка времени t_р(j) - t_p(i) над продолжительностью операции t_ij, т. е.

R_с(i, j) = t_р(j) - t_p(i) - t_ij. (38)

У критических событий ранние и поздние сроки свершения совпадают. Поэтому резерв времени у них равен нулю.

Пример 9. Рассчитать характеристики работ для сетевого графика изображенного на рисунке 3.

Решение.

1. Вычислим характеристики событий по формулам 31 и 32, при этом на рисунке будем отмечать в квадратиках ранний срок наступления события, а в треугольниках поздний срок наступления события (рис. 4).