Тема 6. Метод анализа иерархий
Метод анализа иерархий (МАИ) – методологическая основа для решения задач выбора альтернатив посредством их многокритериального рейтингования. Основное применение метода – поддержка принятия решений посредством иерархической композиции задачи и рейтингования альтернативных решений.
Сбор данных для поддержки принятия решения осуществляется с помощью процедуры парных сравнений, для этого строится множество матриц парных сравнений. Парные сравнения проводятся в терминах доминирования одного элемента над другим. Полученные суждения выражаются в целых числах с учетом девятибалльной шкалы отношений (табл. 3.6).
Матрица
парных сравнений обладает свойством
обратной симметрии (обратно-симметричная
матрица), т.е.
.
Иерархический синтез используется для взвешивания собственных векторов матриц парных сравнений альтернатив весами критериев, имеющихся в иерархии, а также для вычисления суммы по всем соответствующим взвешенным компонентам собственных векторов нижележащего уровня иерархии.
Таблица 3.6
Шкала отношений
Степень значимости |
определение |
1 |
Одинакова значимость |
3 |
Некоторое преобладание |
5 |
Сильная значимость |
7 |
Очень сильная значимость |
9 |
Абсолютная значимость |
2, 4, 6, 8 |
Промежуточные значения между двумя соседними суждениями |
Обратные величины приведенных выше величин |
Если действию i при сравнении с действием j приписывается одно из приведенных выше ненулевых чисел, то действию j при сравнении с действием i приписывается обратное значение |
Один из способов вычисления собственного вектора (W):
Перемножим элементы каждой строки и запишем полученные результаты в столбец.
Извлечем корень n-й степени из каждого элемента найденного столбца.
Складываем элементы этого столбца.
Делим каждый из элементов столбца произведения на полученную сумму.
Для
оценки однородности суждений экспертов
необходимо использовать отклонение
величины максимального собственного
значения
,
от порядка матрицы n.
определяют:
Просуммируем каждый столбец суждений:
.Каждую сумму умножим на соответствующее значение Wi:
.Найдем сумму полученных произведений:
. (28)
В
силу того, что для обратно-симметричных
положительных матриц всегда выполняется
,
то в качестве степени отклонения
положительной обратно-симметричной
матрицы от согласованной берется
показатель индекс однородности (ИО):
. (29)
Однородность суждений оценивается отношением однородности (ОО):
, (30)
где М(ИО) – средние значение индекса однородности случайным образом составленной матрицы парных сравнений, которое основано на экспериментальном материале, представленном в специальной таблице 3.7.
Таблица 3.7
Среднее значение индекса однородности
Порядок матрицы (n) |
М(ИО) |
3 |
0,58 |
4 |
0,9 |
5 |
1,12 |
6 |
1,24 |
7 |
1,32 |
8 |
1,41 |
9 |
1,45 |
10 |
1,49 |
11 |
1,51 |
12 |
1,48 |
13 |
1,56 |
14 |
1,57 |
15 |
1,59 |
В
качестве допустимого используется
значение
.
Если для матрицы парных сравнений
отношение однородности
,
то это свидетельствует о существенном
нарушении логичности суждений, допущенном
экспертами при заполнении матрицы,
поэтому экспертам предлагается
пересмотреть данные, использованные
для построения матрицы, чтобы улучшить
однородность.
Пример 7. Применить метод анализа иерархий для выбора наиболее надежного обеспечения кредита относительно выгод. Декомпозиция задачи приведена на рис. 2.
Решение. Составим матрицу парных сравнений критериев, для этого воспользуемся шкалой отношений (табл. 3.8) и свойствами матрицы парных сравнений.
Вычислим вектор W приоритетов выгод. Для этого, сначала вычислим столбец, который равен произведению элементов соответствующей строки матрицы выгод. Затем извлечем корень n=3-й степени из каждого элемента найденного столбца. Сложим элементы этого столбца. Разделим каждый из этих элементов на полученную сумму (таб. 3.8).
Таблица 3.8
Матрица приоритетов выгод
Выгоды |
1 |
2 |
3 |
Произв. |
корень |
W1 |
1. экономические |
1 |
3,00 |
3,00 |
9,00 |
2,08 |
0,59 |
2. физические |
0,33 |
1 |
2,00 |
0,67 |
0,87 |
0,25 |
3. юридические |
0,33 |
0,50 |
1 |
0,17 |
0,55 |
0,16 |
сумма по столбцам |
1,67 |
4,50 |
6,00 |
|
3,50 |
|
произведение сумм на W1 |
0,99 |
1,12 |
0,94 |
|
|
|
λmax |
3,05 |
|
|
ИО |
0,03 |
|
М(ИО) |
0,58 |
|
|
ОО |
0,05 |
|
После определения W1, вычислим индекс однородности (ИО), для этого, просуммируем каждый столбец суждений. Каждую сумму умножим на соответствующее значение W1. Определим , как сумму полученных произведений (по формуле 28).
Значение М(ИО) берется из таблицы 3.7: т.к., n=3, то М(ИО) = 0,58. Определим индекс однородности ИО (формула 29) и отношение согласованности ОО (формула 30). Отношение согласованности ОО=5%<10%, что говорит о допустимости суждений по данной матрице.
Найдем выгоды, которые являются определяющими при обеспечении кредита. Из таблицы 3.8 видно, что это экономический показатель.
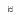
Р
ис.
2. Декомпозиция
задачи выбора наиболее надежного
обеспечения кредита относительно выгод
Критерии второго уровня будем сравнивать попарно по отношению к критериям третьего уровня (таб. 3.9, 3.10, 3.11).
Проделаем все выше описанные процедуры для матрицы экономических выгод, учитывая, что для неё n=3 (таб.3.9).
Таблица 3.9
Матрица экономических выгод
|
1 |
2 |
3 |
Произв. |
корень |
W12 |
1. вероятность увеличения стоимости |
1 |
0,5 |
5 |
2,50 |
1,36 |
0,35 |
2. возврат стоимости |
2 |
1 |
5 |
10,00 |
2,15 |
0,56 |
3. ликвидность |
0,2 |
0,2 |
1 |
0,04 |
0,34 |
0,09 |
сумма по столбцам |
3,20 |
1,70 |
11,00 |
|
3,85 |
|
произведение сумм на W12 |
1,13 |
0,95 |
0,98 |
|
|
|
λmax |
3,05 |
|
|
ИО |
0,03 |
|
М(ИО) |
0,58 |
|
|
ОО |
0,05=5% |
<10%, |
Определим критерий, дающий больший вклад в экономический показатель. Это возврат стоимости.
При составлении матриц физических (таб. 3.10) и юридических выгод (таб. 3.11) необходимо учесть в формулах n=2, т.е., корень вычисляется по второй степени. =2, следовательно, =n, а это значит, что матрицы являются согласованными.
Таблица 3.10
Матрица физических выгод
|
1 |
2 |
Произв. |
корень |
W22 |
1. отсутствие износа |
1,00 |
5,00 |
5,00 |
2,24 |
0,833 |
2. наличие места хранения |
0,20 |
1,00 |
0,20 |
0,45 |
0,167 |
сумма по столбцам |
1,200 |
6,000 |
|
2,68 |
|
произведение сумм на W22 |
1,000 |
1,000 |
|
λmax |
2,00 |
Определим критерий, дающий больший вклад в физический показатель – это отсутствие износа (табл. 3.10).
Определим критерий, дающий больший вклад в юридический показатель - это право требования (табл. 3.11).
Далее необходимо сравнить все виды вложений по каждому критерию третьего уровня (таб. 3.12, 3.13, 3.14, 3.15, 3.16, 3.17, 3.18), схема расчетов повторяется, но n=4, корень берется четвертой степени.
Таблица 3.11
Матрица юридических выгод
|
1 |
2 |
Произв. |
корень |
W32 |
1. право требования |
1 |
4 |
4 |
2 |
0,8 |
2. гарантии на использование |
0,25 |
1 |
0,25 |
0,5 |
0,2 |
сумма по столбцам |
1,25 |
5 |
|
2,50 |
|
произведение сумм на W32 |
1,00 |
1,00 |
|
|
|
λmax |
2,00 |
|
|
|
|
Таблица 3.12
Вероятность увеличения стоимости
|
1 |
2 |
3 |
4 |
Произв. |
корень |
W13 |
1. Иностранная валюта |
1,00 |
1,00 |
4,00 |
7,00 |
28 |
2,30 |
0,44 |
2. Драгоценные металлы |
1,00 |
1,00 |
3,00 |
5,00 |
15 |
1,97 |
0,37 |
3. Ценные бумаги |
0,25 |
0,33 |
1,00 |
3,00 |
0,25 |
0,71 |
0,13 |
4. Недвижимость |
0,14 |
0,20 |
0,33 |
1,00 |
0,01 |
0,31 |
0,06 |
λmax |
4,04 |
|
ИО |
0,01 |
|
|
|
М(ИО) |
0,9 |
|
|
ОО |
0,02=2% |
<10% |
|
Иностранная валюта имеет наивысшую степень вероятности увеличения стоимости по сравнению с другими обеспечениями (из табл. 3.12).
Таблица 3.13
Возврат стоимости
|
1 |
2 |
3 |
4 |
Произв. |
корень |
W23 |
1. Иностранная валюта |
1,00 |
3,00 |
3,00 |
5,00 |
45,00 |
2,59 |
0,51 |
2. Драгоценные металлы |
0,33 |
1,00 |
0,50 |
3,00 |
0,50 |
0,84 |
0,16 |
3. Ценные бумаги |
0,33 |
2,00 |
1,00 |
5,00 |
3,33 |
1,35 |
0,26 |
4. Недвижимость |
0,20 |
0,33 |
0,20 |
1,00 |
0,01 |
0,34 |
0,07 |
λmax |
4,15 |
|
ИО |
0,05 |
|
|
|
М(ИО) |
0,9 |
|
|
ОО |
0,06=6% |
<10% |
|
Из таблицы 3.13 можно сделать вывод, что иностранная валюта имеет наивысшую степень возврата стоимости по сравнению с другими обеспечениями.
Таблица 3.14
Ликвидность
|
1 |
2 |
3 |
4 |
Произв. |
корень |
W33 |
1. Иностранная валюта |
1,00 |
3,00 |
5,00 |
5,00 |
75,00 |
2,94 |
0,55 |
2. Драгоценные металлы |
0,33 |
1,00 |
3,00 |
3,00 |
3,00 |
1,32 |
0,25 |
3. Ценные бумаги |
0,20 |
0,33 |
1,00 |
3,00 |
0,20 |
0,67 |
0,13 |
4. Недвижимость |
0,20 |
0,33 |
0,33 |
1,00 |
0,02 |
0,39 |
0,07 |
λmax |
4,16 |
|
ИО |
0,05 |
|
|
|
М(ИО) |
0,9 |
|
|
ОО |
0,06=6% |
<10% |
|
Из таблицы 3.14 можно сделать вывод, что иностранная валюта имеет наивысшую степень ликвидности по сравнению с другими обеспечениями.
Таблица 3.15
Отсутствие износа
|
1 |
2 |
3 |
4 |
Произв. |
корень |
W43 |
1. Иностранная валюта |
1,00 |
1,00 |
5,00 |
5,00 |
25,00 |
2,24 |
0,45 |
2. Драгоценные металлы |
1,00 |
1,00 |
3,00 |
3,00 |
9,00 |
1,73 |
0,35 |
3. Ценные бумаги |
0,20 |
0,33 |
1,00 |
2,00 |
0,13 |
0,60 |
0,12 |
4. Недвижимость |
0,20 |
0,33 |
0,50 |
1,00 |
0,03 |
0,43 |
0,09 |
λmax |
4,09 |
|
|
|
ИО |
0,03 |
|
М(ИО) |
0,9 |
|
|
|
ОО |
0,03=3% |
<10% |
Из таблицы 3.15 можно сделать вывод, что иностранная валюта имеет наивысшую степень к проявлению отсутствия износа по сравнению с другими обеспечениями.
Из таблицы 3.16 можно сделать вывод, что иностранная валюта имеет наивысшую степень наличие места по хранению по сравнению с другими обеспечениями.
Из таблицы 3.17 можно сделать вывод, что драгоценные металлы имеют наивысшую степень законодательно оформленного права требования по сравнению с другими обеспечениями.
Таблица 3.16
Наличие места для хранения
|
1 |
2 |
3 |
4 |
Произв. |
корень |
W53 |
1. Иностранная валюта |
1,00 |
1,00 |
1,00 |
5,00 |
5,00 |
1,50 |
0,33 |
2. Драгоценные металлы |
1,00 |
1,00 |
1,00 |
3,00 |
3,00 |
1,32 |
0,29 |
3. Ценные бумаги |
1,00 |
1,00 |
1,00 |
3,00 |
3,00 |
1,32 |
0,29 |
4. Недвижимость |
0,20 |
0,33 |
0,33 |
1,00 |
0,02 |
0,39 |
0,09 |
λmax |
4,03 |
|
ИО |
0,01 |
|
|
|
М(ИО) |
0,9 |
|
|
ОО |
0,01=1% |
<10% |
|
Таблица 3.17
Законодательно оформленное право требования
|
1 |
2 |
3 |
4 |
Произв. |
корень |
W63 |
1. Иностранная валюта |
1,00 |
1,00 |
2,00 |
2,00 |
4,00 |
1,41 |
0,31 |
2. Драгоценные металлы |
1,00 |
1,00 |
3,00 |
3,00 |
9,00 |
1,73 |
0,38 |
3. Ценные бумаги |
0,50 |
0,33 |
1,00 |
3,00 |
0,50 |
0,84 |
0,19 |
4. Недвижимость |
0,50 |
0,33 |
0,33 |
1,00 |
0,06 |
0,49 |
0,11 |
λmax |
4,11 |
|
ИО |
0,04 |
|
|
|
М(ИО) |
0,9 |
|
|
ОО |
0,04=4% |
<10% |
|
Таблица 3.18
Гарантии на использование имущества
|
1 |
2 |
3 |
4 |
Произв. |
корень |
W73 |
1. Иностранная валюта |
1,00 |
3,00 |
5,00 |
5,00 |
75,00 |
2,94 |
0,57 |
2. Драгоценные металлы |
0,33 |
1,00 |
2,00 |
3,00 |
2,00 |
1,19 |
0,23 |
3. Ценные бумаги |
0,20 |
0,50 |
1,00 |
1,00 |
0,10 |
0,56 |
0,11 |
4. Недвижимость |
0,20 |
0,33 |
1,00 |
1,00 |
0,07 |
0,51 |
0,10 |
λmax |
4,03 |
|
|
|
|
|
|
М(ИО) |
0,9 |
|
ИО |
0,01 |
|
ОО |
0,01 |
Из таблицы 3.18 можно сделать вывод, что иностранная валюта имеет наивысшие гарантии на использование имущества по сравнению с другими обеспечениями.
Определяем альтернативу, наиболее подходящую с экономической точки зрения.
=
(
)*
.
=
*
=
.
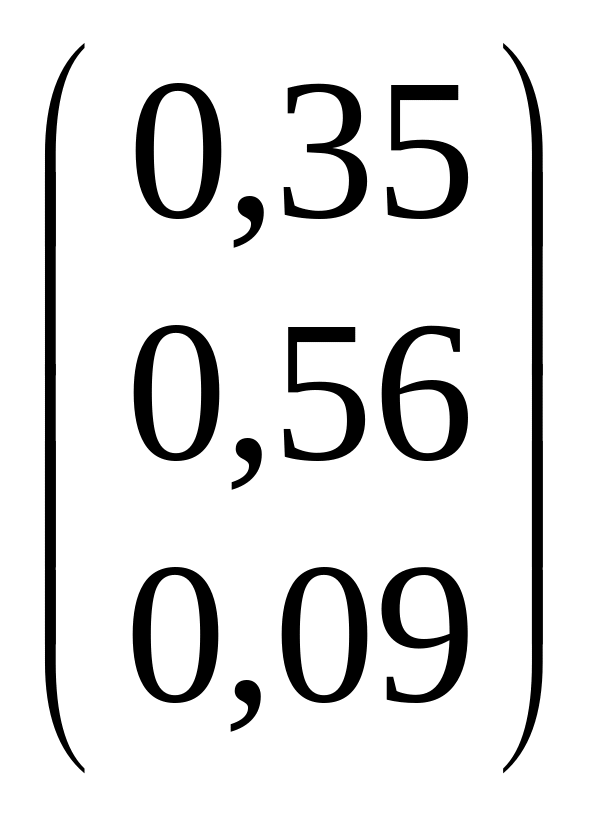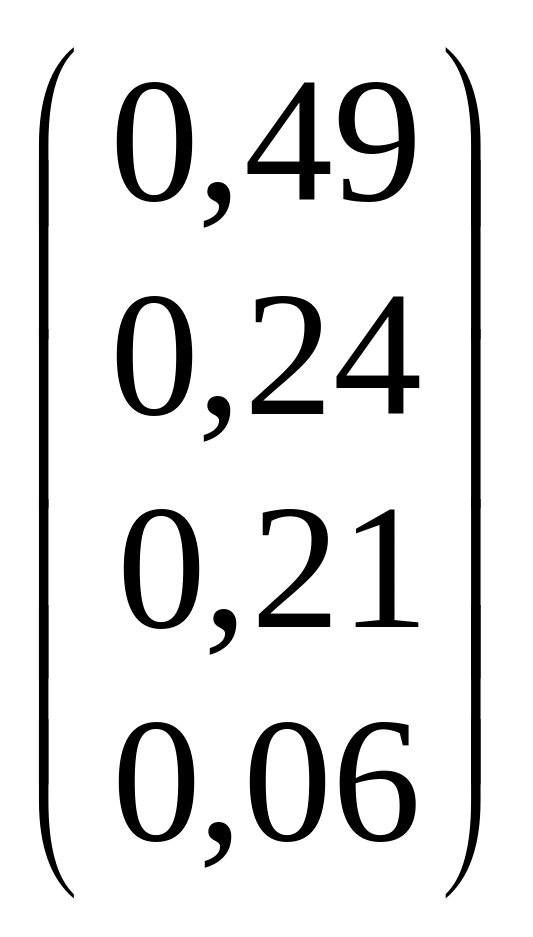Определяем альтернативу, наиболее подходящую с физической точки зрения.
=
*
.
=
*
=
.
Определяем альтернативу, наиболее подходящую с юридической точки зрения.
=
*
.
=
*
=
.
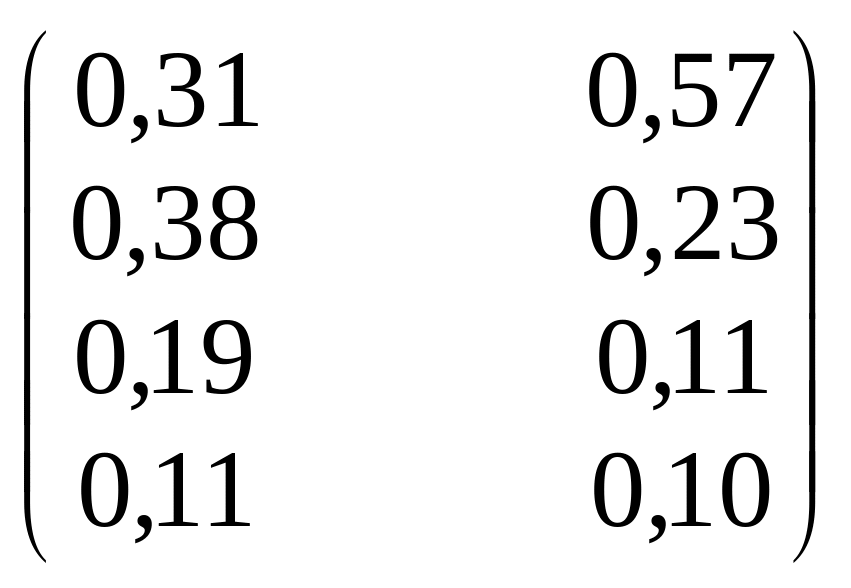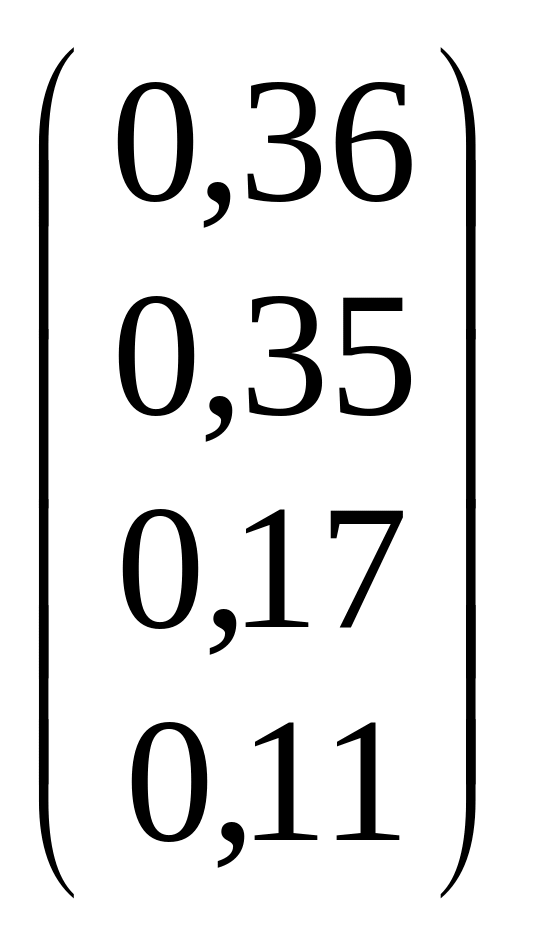Определяем альтернативу, удовлетворяющую всем критериям.
W
=
*
.
W
=
*
=
.
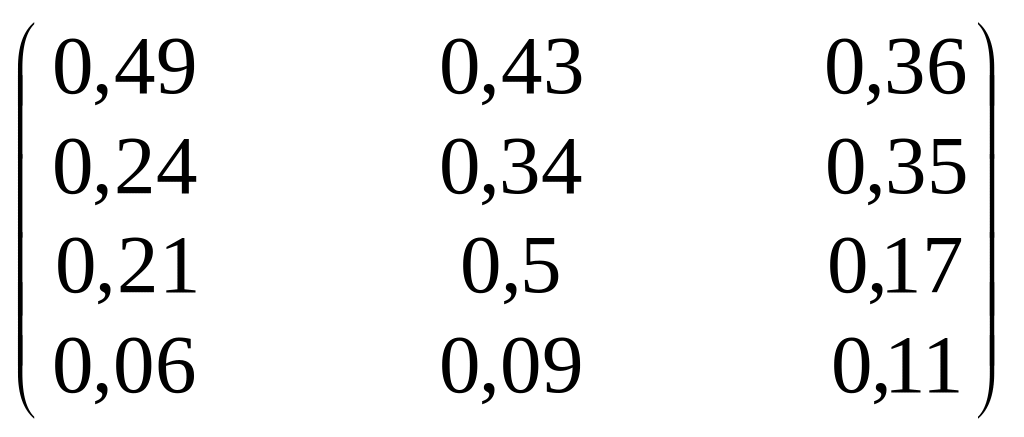Вычислив глобальные приоритеты всех видов вложений, делаем вывод о предпочтительности иностранной валюты.