Задания третьего поточного контроля
Задача 1.
В приведенной
далее таблице 4
для каждого варианта указаны значения
параметров целевой функции задачи
нелинейного программирования (ЗНП) и
координаты вершин
выпуклого многоугольника, задающего
множество допустимых точек ЗНП, причем
целевая функция
задана в виде
,
,
,
,
а ЗНП поставлена на максимум.
Выполнить следующие задания:
восстановить математическую модель ЗНП, воспользовавшись данными Таблицы 4;
выполнить две итерации методом линеаризации, взяв в качестве начальной точку
.
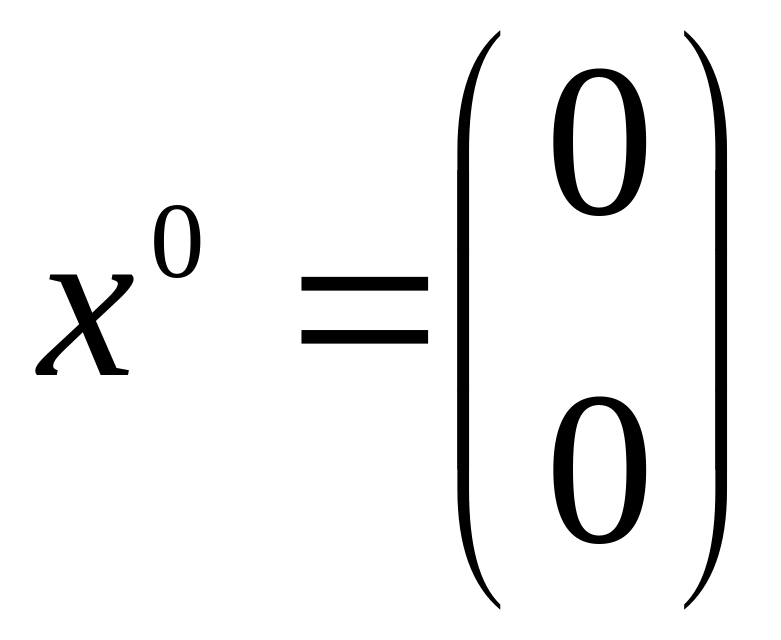Таблица 4
Данные для решения задач 1 и 2 третьего поточного контроля
Вариант |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
-6 |
3 |
3 |
-9 |
4 |
9 |
1 |
0 |
0 |
0 |
12 |
14 |
4 |
13 |
12 |
8 |
13 |
14 |
0 |
2 |
-10 |
7 |
7 |
-13 |
8 |
9 |
-1 |
0 |
0 |
0 |
5 |
4 |
15 |
15 |
8 |
12 |
11 |
15 |
0 |
3 |
-10 |
7 |
7 |
-13 |
1 |
1 |
-9 |
0 |
0 |
0 |
2 |
5 |
13 |
14 |
8 |
6 |
15 |
14 |
0 |
4 |
-6 |
3 |
3 |
-9 |
2 |
8 |
-6 |
0 |
0 |
0 |
4 |
14 |
3 |
3 |
6 |
12 |
9 |
14 |
0 |
5 |
-8 |
5 |
5 |
-11 |
2 |
3 |
3 |
0 |
0 |
0 |
3 |
15 |
4 |
5 |
9 |
9 |
10 |
15 |
0 |
6 |
-8 |
5 |
5 |
-11 |
8 |
7 |
-7 |
0 |
0 |
0 |
11 |
15 |
9 |
10 |
11 |
1 |
12 |
15 |
0 |
7 |
-4 |
1 |
1 |
-7 |
3 |
9 |
-10 |
0 |
0 |
0 |
9 |
12 |
10 |
3 |
14 |
15 |
2 |
15 |
0 |
8 |
-6 |
3 |
3 |
-9 |
2 |
4 |
-1 |
0 |
0 |
0 |
1 |
8 |
12 |
11 |
3 |
5 |
15 |
11 |
0 |
9 |
-10 |
7 |
7 |
-13 |
7 |
7 |
-4 |
0 |
0 |
0 |
1 |
14 |
3 |
5 |
7 |
13 |
12 |
14 |
0 |
10 |
-6 |
3 |
3 |
-9 |
6 |
8 |
-1 |
0 |
0 |
0 |
8 |
4 |
11 |
2 |
10 |
5 |
11 |
7 |
0 |
11 |
-8 |
5 |
5 |
-11 |
3 |
7 |
1 |
0 |
0 |
0 |
3 |
8 |
15 |
9 |
15 |
3 |
14 |
13 |
0 |
12 |
-4 |
1 |
1 |
-7 |
4 |
3 |
2 |
0 |
0 |
0 |
12 |
7 |
15 |
15 |
4 |
11 |
15 |
15 |
0 |
13 |
-13 |
10 |
10 |
-16 |
6 |
6 |
-10 |
0 |
0 |
0 |
7 |
15 |
8 |
3 |
12 |
12 |
10 |
15 |
0 |
14 |
-7 |
4 |
4 |
-10 |
6 |
6 |
8 |
0 |
0 |
0 |
3 |
3 |
14 |
4 |
14 |
8 |
10 |
8 |
0 |
15 |
-4 |
1 |
1 |
-7 |
7 |
10 |
-9 |
0 |
0 |
0 |
1 |
4 |
8 |
11 |
11 |
7 |
10 |
14 |
0 |
16 |
-10 |
7 |
7 |
-13 |
6 |
2 |
-5 |
0 |
0 |
0 |
1 |
10 |
13 |
9 |
15 |
3 |
15 |
12 |
0 |
17 |
-8 |
5 |
5 |
-11 |
5 |
10 |
-4 |
0 |
0 |
0 |
3 |
7 |
14 |
14 |
2 |
3 |
15 |
14 |
0 |
18 |
-12 |
9 |
9 |
-15 |
5 |
3 |
-9 |
0 |
0 |
0 |
3 |
10 |
5 |
4 |
13 |
1 |
14 |
11 |
0 |
19 |
-11 |
8 |
8 |
-14 |
6 |
4 |
3 |
0 |
0 |
0 |
1 |
6 |
5 |
9 |
5 |
11 |
1 |
11 |
0 |
20 |
-7 |
4 |
4 |
-10 |
4 |
8 |
8 |
0 |
0 |
0 |
6 |
10 |
8 |
8 |
15 |
3 |
12 |
12 |
0 |
Задача 2. Для поставленной в Задаче 1 настоящего задания задачи нелинейного программирования выполнить следующие действия:
1) проверить, является ли данная задача задачей выпуклого программирования, и выполнены ли условия теоремы Куна-Таккера;
2) проверить точки , координаты которых указаны в Таблице 4, на оптимальность, используя теорему Куна-Таккера.
Задача 3. Найти кратчайший путь в приведенном для каждого варианта графе с помощью метода динамического программирования.
Вариант 1 |
Вариант 2 |
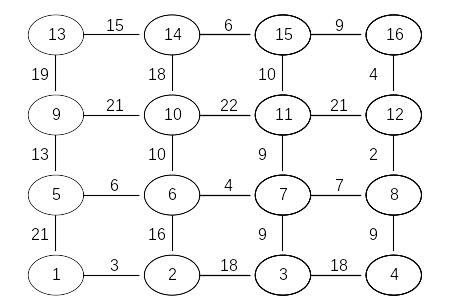
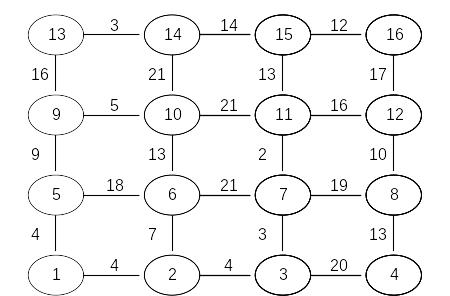
Вариант 3 |
Вариант 4 |
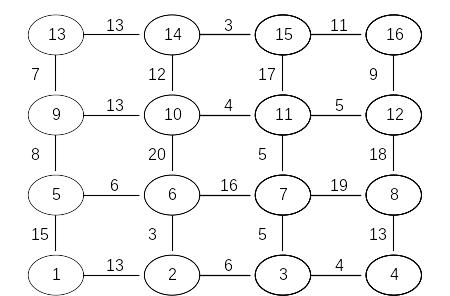
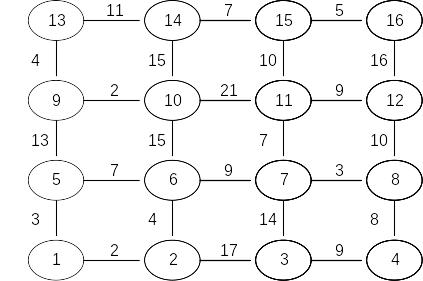
Вариант 5 |
Вариант 6 |
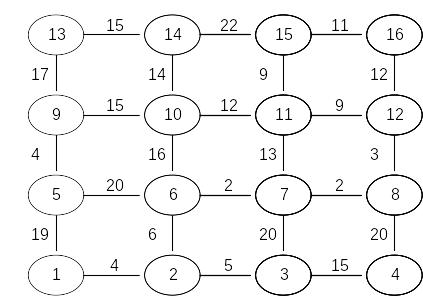
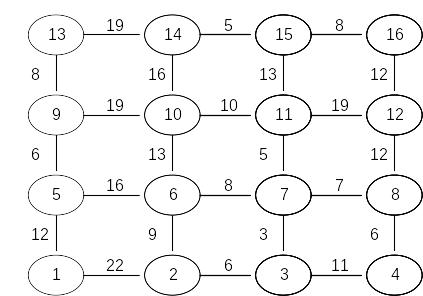
Вариант 7 |
Вариант 8 |
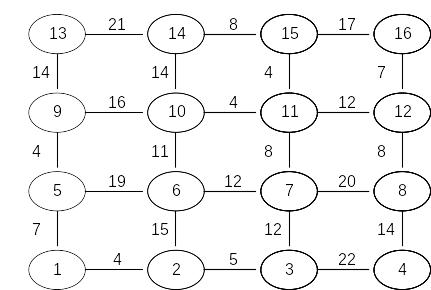
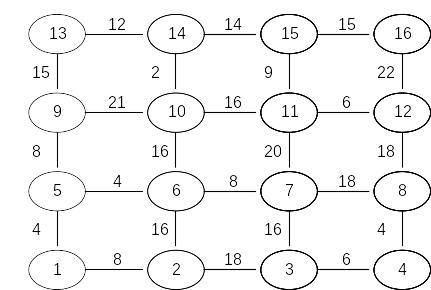
Вариант 9 |
Вариант 10 |
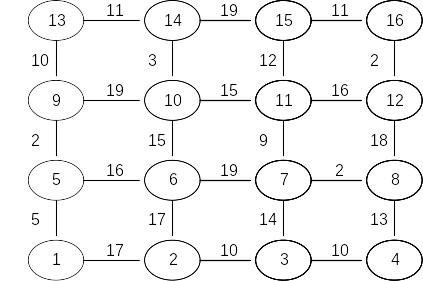
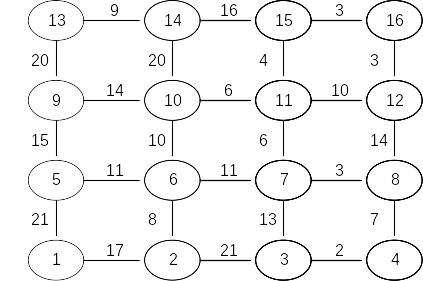
Вариант 11 |
Вариант 12 |
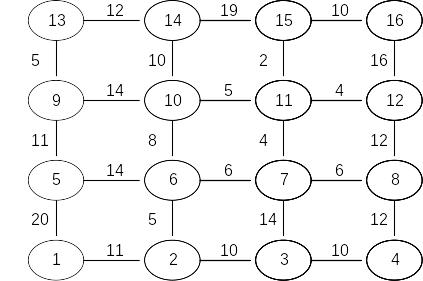
Вариант 13 |
Вариант 14 |
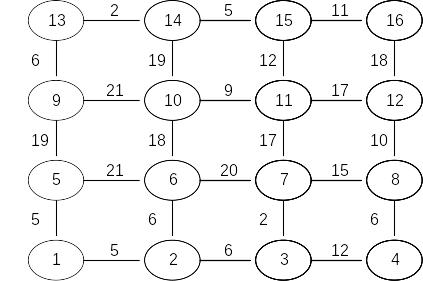
Вариант 15 |
Вариант 16 |
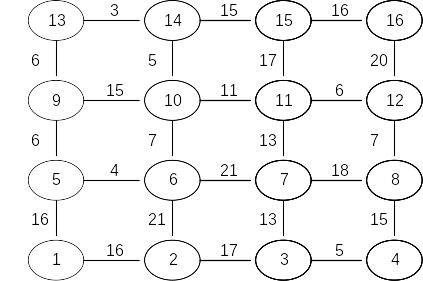
Вариант 17 |
Вариант 18 |
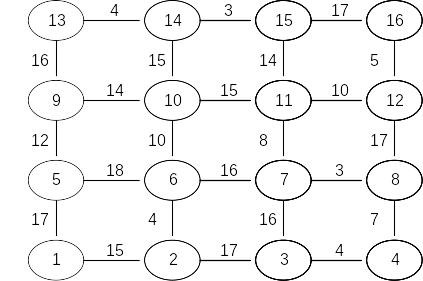
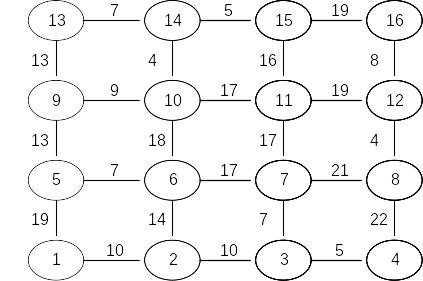
Вариант 19 |
Вариант 20 |
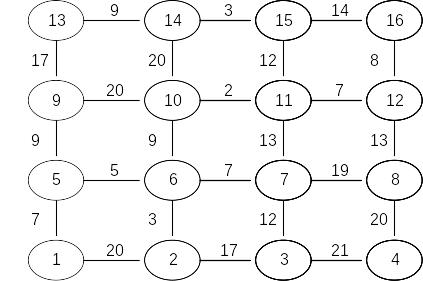
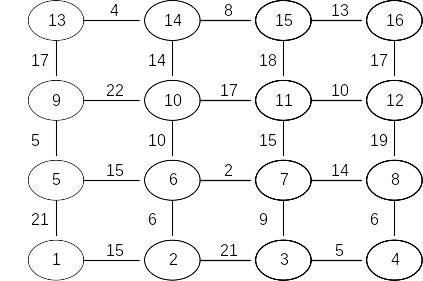
Задача 4. Найти оптимальный маршрут для задачи коммивояжера, заданной таблицей, с помощью метода ветвей и границ.
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
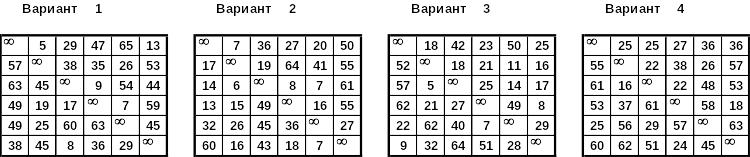
Вариант 5 |
Вариант 6 |
Вариант 7 |
Вариант 8 |
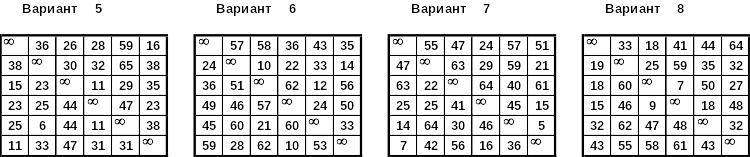
Вариант 9 |
Вариант 10 |
Вариант 11 |
Вариант 12 |
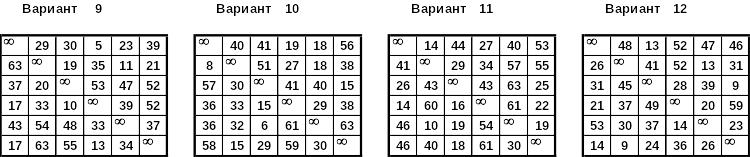
Вариант 13 |
Вариант 14 |
Вариант 15 |
Вариант 16 |
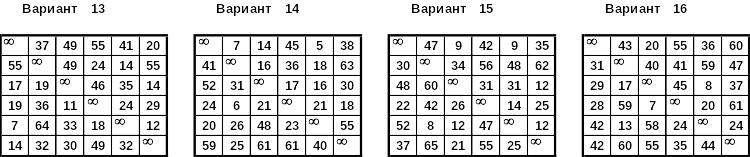
Вариант 17 |
Вариант 18 |
Вариант 19 |
Вариант 20 |
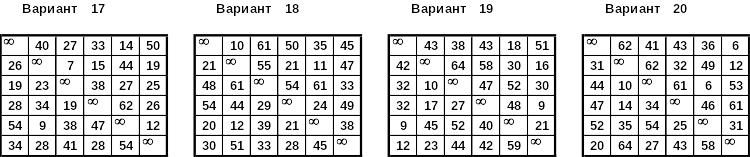
Задача 5.
Для каждого варианта в приведенной
далее Таблице 5 указаны номера задач
из пунктов 5.1) – 5.5) соответственно,
которые необходимо выполнить.
5.1) Вычислить производную функции:
1.
2.
3.
4.
5.
6.
7.
8.
5.2) Вычислить производную функции:
1.
. 2.
. 3.
.
4.
. 5.
. 6.
.
7.
. 8.
.
5.3) Вычислить неопределенный интеграл:
1.
. 2.
3.
.
4.
5.
. 6.
7.
. 8.
5.4) Вычислить неопределенный интеграл:
1.
. 2.
. 3.
.
4.
. 5.
. 6.
.
7.
. 8.
.
5.5) Решить краевую задачу:
1.
. 2.
.
3.
. 4.
.
5.
. 6.
.
7.
. 8.
.
Таблица 5