8. Формулы полной вероятности и Байеса.

Одним из следствий совместного применения теорем сложения и умножения вероятностей являются формулы полной вероятности и Байеса. Напомним, что события A₁, A₂, …, A_n образуют полную группу, если A_i ∙ A_j = Ø, i ≠ j и 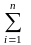A_i = Ω. Систему таких событий называют также разбиением.

Теорема. Пусть событий H₁, H₂, …, H_n образуют полную группу. Тогда для любого, наблюдаемого в опыте, события A имеет место формула полной вероятности или средней вероятности.

P(A) = P(H_i) ∙ P(A|H_i).

Так как H₁ + H₂ + … + H_n = Ω, то в силу свойств операций над событиями,

A = A ∙ Ω = A ∙ (H₁ + H₂ + … + H_n ) = A ∙ H₁ + A ∙ H₂ + … + A ∙ H_n . Из того, что H_i ∙ H_j = Ø, следует, что (A ∙ H_i) ∙ (A ∙ H_j) = Ø, i ≠ j, т. е. события A ∙ H_i и A ∙ H_j также несовместны. Тогда по теореме сложения вероятностей P(A) = P(A ∙ H₁ ) + P(A ∙ H₂) +…+ P(A ∙ H_n) т. е. P(A)= P(A ∙ H_i ). По теореме умножения вероятностей P(A ∙ H_i ) = P(H_i) ∙ P(A|H_i), откуда и следует формула теоремы.

Отметим, что в формуле события H₁, H₂, …, H_n называют гипотезами; они исчерпывают все возможные предположения (гипотезы) относительно исходов как бы первого этапа опыта, событие A – один из возможных исходов второго этапа.

Следствием формулы полной вероятности является формула Байеса или теорема гипотез. Она позволяет переоценить вероятности гипотез H_i , принятых до опыта и называемых априорными по результатам уже проведенного опыта, т. е. найти условные вероятности P(A|H_i), которые называют апостериорными.

Теорема. Пусть события H₁, H₂, …, H_n образуют полную группу событий. Тогда условная вероятность событий H_k (k = ) при условии, что событие A произошло, задается формулой

P(H_k|A) = 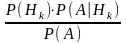, где P(A) = P(H₁) ∙ P(A|H₁) +…+ P(H_n) ∙ P(A|H_n) – формула полной вероятности. Формула называется формулой Байеса.

Применив формулу условной вероятности и умножения вероятностей, имеем

P(H_k|A) = = , где P(A) – формула полной вероятности.

9. Повторные независимые испытания. Формула Бернулли.

Независимые испытания. Схема Бернулли.

С понятием «независимых событий» связано понятие «независимых испытаний (опытов)».

Несколько опытов называются независимыми, если их исходы представляют собой независимые испытания (независимые в совокупности).

Другими словами, если проводится несколько испытаний, т. е. опыт выполняется при данном комплексе условий многократно (такое явление называется «последовательностью испытаний»), причем вероятность наступления некоторого события A в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми.

При практическом применении теории вероятностей часто используется стандартная схема, называемая схемой Бернулли или схемой независимых испытаний.

Последовательность n независимых испытаний, в каждом из которых может произойти некоторое событие A (его называют успехом) с вероятностью P(A) = p или противоположное ему событие A̅ (его называют неудачей) с вероятностью P(A̅) = q = 1 – p, называется схемой Бернулли.

В каждом испытании ПЭС состоит только из двух элементарных событий, т. е. Ω = {ω₀, ω₁}, где ω₀ – неудача, ω₁ – успех, при этом A = {ω₁}, A̅ = {ω₀}. Вероятность этих событий обозначается через p и q соответственно (p + q = 1). Множество элементарных исходов для n опытов состоит из 2ⁿ элементов. Например, при n = 3, т. е. опыт повторяется 3 раза, Ω = {(A̅, A̅, A̅) / ω₀ ; (A, A, A̅) / ω₁ ; (A, A̅, A) / ω₂ ; (A̅, A, A) / ω₃ ;(A, A̅, A̅) / ω₄ ; (A̅, A, A̅) / ω₅ ;( A̅, A̅, A) / ω₆ ;(A, A, A) / ω₇ }. Вероятность каждого элементарного события определяется однозначно. По теореме умножения вероятность события, скажем ω₆ = ( A̅, A̅, A), равна q ∙ q ∙ p = pq² , события ω₇ – p ∙ p ∙ p = p³q⁰ =p³ и т. д.

Часто успеху сопоставляется число 1, неудаче – число 0. элементарным событием для n опытов будет последовательность из n нулей и единиц. Тройка чисел (0, 0, 0,) означает, что во всех трех опытах событие A не наступило; тройка чисел (0, 1, 0) означает, что событие A наступило во втором опыте, а в первом и третьем – не наступило.

Формула Бернулли.

Простейшая задача, относящаяся к схеме Бернулли, состоит в определении вероятности того, что в n независимых испытаниях событие A наступит m раз (0 ≤ m ≤ n). Обозначается искомая вероятность так: P_n(m) или P_n,m или P(μ_n = m), где μ_n – число появления события A в серии из n опытов.

Теорема. Если производится n независимых испытаний, в каждом из которых вероятность появления события A равна p, а вероятность его непоявления равна q = 1 – p, то вероятность того, что событие A произойдет m раз, определяется формулой Бернулли

P_n(m) = C ∙ p^m ∙ q^n–m , m = 0, 1, …, n.

Вероятность одного сложного события, состоящего в том, что событие A в n независимых опытах появится m раз в первых m опытах и не появится (n – m) раз в остальных опытах (это событие ) по теореме умножения вероятностей равна p^m ∙ q^n–m . Вероятность появления события A снова m раз, но в другом порядке, будет той же самой, т.е.p^m∙q^n–m .

Число таких сложных событий – в n опытах m раз встречается событие A в различном порядке – равно числу сочетаний из n по m, т. е. C . Так как все сложные события несовместны, то по теореме сложения вероятностей искомая вероятность равна сумме вероятностей всех возможных сложных событий, т. е. P_n(m) = = C ∙ p^m ∙ q^n–m , m = 0, 1, …, n.

Можно заметить, что вероятности P_n(m), m = 0, 1, …, n являются коэффициентами при x^m в разложении (q + px)ⁿ по формуле бинома Ньютона:

(q + px)ⁿ = qⁿ + C q^n–1 px + C q^n–2 p²x² +…+ C q^n–m p^m x^m +…+ pⁿ xⁿ . Поэтому совокупность вероятностей P_n(m) называют биноминальным законом распределения вероятностей, а функцию φ(x) = (q + px)ⁿ – производящей функцией для последовательности независимых опытов.

Если в каждом из независимых испытаний вероятности наступления события A разные, то вероятность того, что событие A наступит m раз в n опытах, равна коэффициенту при m-ой степени многочлена φ_n (z)=(q₁ + p₁z)(q₂ + p₂z) ∙…∙ (q_n + p_nz), где φ_n (z) – производящая функция.

Если в серии из n независимых опытов, в каждом из которых может произойти одно и только одно из k событий A₁, A₂, …, A_k с соответствующими вероятностями p₁, p₂, …, p_k , то вероятность того, что в этих опытах событие A₁ появится m₁ раз, событие A₂ – m₂ раз, …, событие A_k – m_k раз, равна

P_n(m₁, m₂, …, m_k) = , где m₁ + m₂ +…+ m_k = n. Вероятности называются полиномиальным распределением.