
- •Вариант 1.
- •Вариант 2.
- •Вариант 3.
- •Вариант 4.
- •Вариант 5.
- •Вариант 6.
- •Вариант 7.
- •Вариант 8.
- •Вариант 9.
- •Вариант 10.
- •Вариант 11.
- •Вариант 12.
- •Вариант 13.
- •Вариант 14.
- •Вариант 15.
- •Вариант 16.
- •Вариант 17.
- •Вариант 18.
- •Вариант 19.
- •Вариант 20.
- •Вариант 21.
- •Вариант 22.
- •Вариант 23.
- •Вариант 24.
- •Вариант 25.
- •Вариант 26.
- •Вариант 27.
- •Вариант 28.
- •Вариант 29.
- •Вариант 30.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Малаховский Н.В.
Методические указания и контрольная работа
«Функции нескольких переменных»
для студентов заочного отделения
Калининград, 2012
Правила выполнения контрольной работы
В соответствии с учебным планом студенты заочного отделения выполняют индивидуальные работы по курсу «Математика» и сдают зачёт или экзамен.
Контрольную работу необходимо выполнять в тетради синими чернилами, оставляя поля для замечаний преподавателя.
Контрольная работа должна содержать титульный лист установленного образца (см. Приложение).
Контрольная работа должна содержать решение всех задач, указанных в задании, строго по своему варианту. Контрольная работа, содержащая решение не всех задач, а так же решение задач не своего варианта, не засчитывается.
Решения задач следует располагать в порядке номеров, указанных в работе, сохраняя номера задач.
Перед решением каждой задачи необходимо написать полностью ее условие. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения.
Каждая контрольная работа состоит из 30 задач. Номер задачи выбирается по номеру студента в списке группы в журнале.
Если студент испытывает затруднения в усвоении теоретического и практического материала, то он может получить консультацию у преподавателя кафедры «Естественно-научных и технических дисциплин».
Выполненную и надлежащим образом оформленную контрольную работу студент передаёт специалисту учебно-методического отдела для регистрации.
В прорецензированной контрольной работе студент должен исправить все отмеченные преподавателем ошибки и учесть рекомендации. Если работа не зачтена, то после исправления ошибок она отправляется на повторную проверку.
Зачтённые контрольные работы предъявляются студентом при сдаче зачёта или экзамена.
Вариант 1.
Вычислить частные производные
 и
и
 для функции:
для функции:
 .
.Оценить абсолютную и относительные погрешности при вычислении значения функции
 при
при
 ,
,
 .
.Написать формулы для производных
 и
и
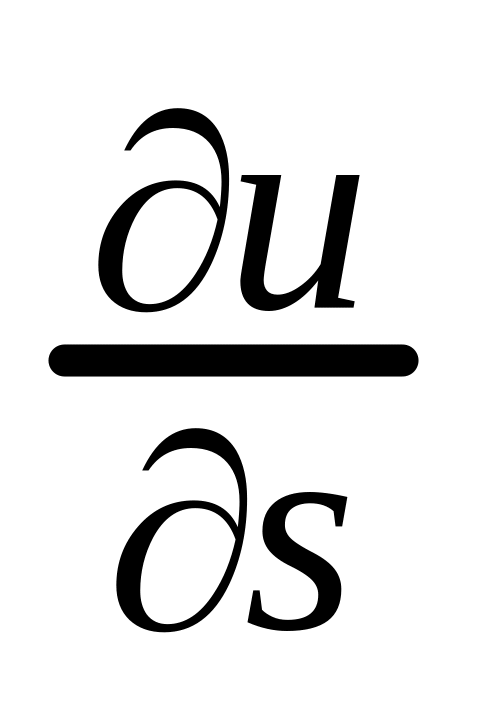 для функции
для функции
 , если
, если
 .
.Найти все частные производные второго порядка для функции
 .
.Вычислить
 для функции
для функции
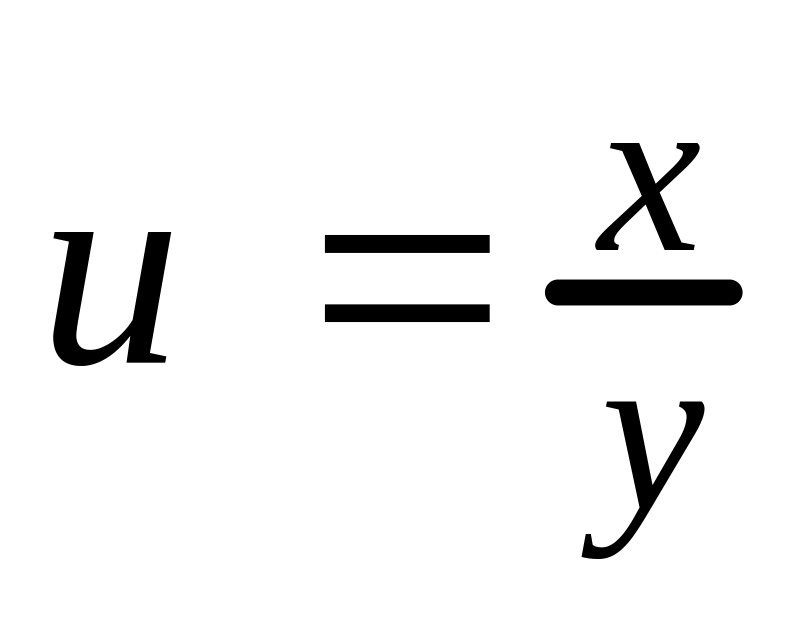 .
.Вычислить
 и
и
 для функции
для функции
 ,
заданной неявно
,
заданной неявно
 .
.Найти частные производные и для функции
 ,
заданной неявно
,
заданной неявно
 .
.Вычислить
 ,
,
 ,
,
 и
и
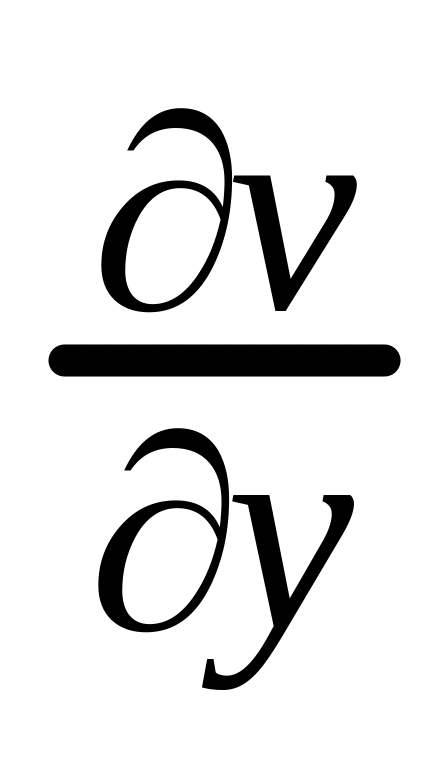 для функций
для функций
 и
и
 ,
заданных параметрически
,
заданных параметрически
 .
.Написать уравнение касательной плоскости и нормали к поверхности, заданной уравнением
 в точке
в точке
 .
.Исследовать на экстремум функцию
 .
.Найти значения функции , заданной неявно зависимостью
 ,
в стационарных точках.
,
в стационарных точках.Найти наибольшее и наименьшее значения функции
 в области
в области
 ,
,
 .
.Данное положительное число
 разложить на
разложить на
 положительных сомножителей так, чтобы
сумма обратных их величин была наименьшей.
положительных сомножителей так, чтобы
сумма обратных их величин была наименьшей.
Вариант 2.
Вычислить и для функции:
 .
.Оценить абсолютную и относительные погрешности при вычислении значения функции
 при
при
 ,
,
 .
.Написать формулы для производных и для функции
 , если
, если
 .
.Найти все частные ,, второго порядка для функции
 .
.Найти для функции
 .
.Найти
 и
и
 для функции
,
заданной неявно
для функции
,
заданной неявно
 .
.Найти частные производные и для функции , заданной неявно
 .
.Вычислить , , и для функций и , заданных параметрически
 .
.Написать уравнение касательной плоскости и нормали к поверхности, заданной уравнением
 в точке
в точке
 .
.Исследовать на экстремум функцию
 при
при
 ,
,
 .
.Найти значения функции , заданной неявно
 ,
в стационарных точках.
,
в стационарных точках.Найти наибольшее и наименьшее значения функции
 в области
в области .
.При каких размерах открытая прямоугольная ванна данной вместимости
 имеет наименьшую поверхность.
имеет наименьшую поверхность.
Вариант 3.
Вычислить
 и
и
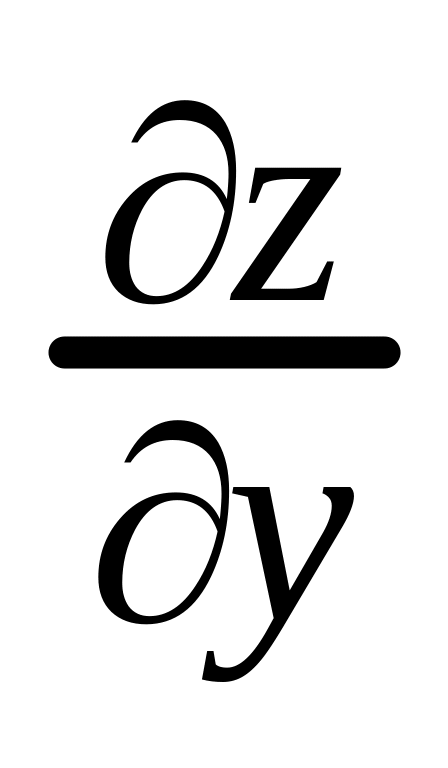 для функции:
для функции:
 .
.Оценить абсолютную и относительные погрешности при вычислении значения функции
 ,
при
,
при
 .
.Вычислить
 и
и
 ,
если
,
если
 ,
,
 .
.Вычислить все частные производные второго порядка для функции
 .
.Вычислить для функции
 .
.Вычислить и для функции
 заданной неявно:
заданной неявно: .
.Функция
 задана неявно:
задана неявно:
 .
Вычислить частные производные
и
.
.
Вычислить частные производные
и
.Функции
 и
и
 заданы параметрически:
заданы параметрически:
 .
Вычислить частные производные
.
Вычислить частные производные
 ,
,
 ,
,
 и
и
 .
.Написать уравнения касательной плоскости и нормали к поверхности, заданной уравнением
 ,
в точке
,
в точке
 .
.Исследовать функцию
 на экстремум.
на экстремум.Найти значения функции
 ,
заданной неявно зависимостью
,
заданной неявно зависимостью
 ,
в стационарных точках.
,
в стационарных точках.Найти наибольшее и наименьшее значения функции
 в области, заданной неравенством
в области, заданной неравенством
 .
.При каких размерах открытая цилиндрическая ванна с полукруглым поперечным сечением, поверхность которой равна S , имеет наибольшую вместимость ?
