3.4.4. Обобщенные характеристики электрических цепей

В ряде случаев при определении отклика цепи удобно использовать обобщенные характеристики цепи, которые являются откликом на некие тестовые входные сигналы того или иного рода.

Мы уже говорили об откликах цепи на тестовый сигнал в виде гармонического сигнала единичной амплитуды и нулевой начальной фазы. Эту обобщенную характеристику мы называли комплексным коэффициентом передачи .

Мы чисто формально ввели операторную передаточную функцию, получив ее путем простой замены величины jω в комплексном коэффициенте передачи на величину s. Теперь можно уточнить, что передаточной функцией называется отношение изображения выходного сигнала к изображению входного сигнала при нулевых начальных условиях в цепи. Т. е. передаточная функция представляет некий отклик электрической цепи на стандартный гармонический сигнал, представленный в операторной форме и полученный для случая комплексной частоты .

Важными обобщенными характеристиками электрической цепи являются переходная и импульсная характеристики характеристика.

Под переходной характеристикой электрической цепи h(t) понимается отклик электрической цепи, которая не имеет начального запаса энергии на реактивных элементах (т.е. с нулевыми начальными условиями) на действие единичной функции включения (функции Хевисайда).

Под импульсной характеристикой электрической цепи h(t) понимается отклик электрической цепи, которая не имеет начального запаса энергии на реактивных элементах (т.е. с нулевыми начальными условиями) на действие δ – импульса Дирака.

Обобщенные характеристики электрической цепи связаны друг с другом, что облегчает их расчет.

Задача нахождения импульсной характеристики сводится к расчету переходного процесса при δ – импульсном воздействии. Проще такой расчет выполнить операторным методом. Так как преобразование Лапласа от δ – импульса Дирака равно единице, то получается замечательный результат: L – изображением импульсной характеристики является операторная передаточная функция, и чтобы найти импульсную характеристику достаточно взять обратное преобразование Лапласа от операторной передаточной функции.

Таким образом, для определения импульсной характеристики необходимо найти: 1) операторную передаточную функцию; 2) обратное преобразование Лапласа от операторной передаточной функции.

Задача расчета переходной характеристики сводится к расчету цепи операторным методом. Учитывая, что L – изображение единичной функции Хевисайда равно 1/s, то получается, что для того, чтобы найти переходную характеристику достаточно взять обратное преобразование Лапласа от операторной передаточной функции, деленной на s.

Таким образом, для определения переходной характеристики необходимо найти: 1)операторную передаточную функцию; 2) обратное преобразование Лапласа от операторной передаточной функции, деленной на s.

Взаимосвязь обобщенных характеристик можно выразить в виде сводки формул:

(3.73)

(3.74)

(3.75)

(3.76)

(3.77)

Здесь h(t), H(s)– переходная характеристика и ее операторное изображение;

g(t),g(s)- импульсная характеристика и ее операторное изображение;

K(s) – операторная передаточная функция.

Следует иметь в виду, что существует и взаимосвязь между предельными значениями обобщенных характеристик.

Значение переходной характеристики при t =0 равно значению АЧХ на бесконечной частоте

(3.78)

Значение переходной характеристики после окончания переходного процесса равно значению АЧХ на нулевой частоте

(3.79)

3.5. Трехфазные и магнитные цепи

3.5.1. Трехфазные цепи

В настоящее время почти все электроснабжение, включающее производство, передачу и распределение огромного количества электрической энергии, осуществляется с помощью трехфазных цепей. В таких цепях генератор, являющийся преобразователем механической энергии в энергию электрическую, вырабатывает три гармонических напряжения равных амплитуд. Фазы же этих напряжений сдвинуты относительно друг друга на угол 120° (2π/3), что осуществляется за счет поворота на тот же угол трех обмоток статора генератора (оси обмоток статора смещены в пространстве на 120). С ротором генератора связано постоянное магнитное поле, вращающееся вместе с ротором с постоянной угловой скоростью. В результате образуются три гармонических напряжения:

Эти функции называют фазными напряжениями

Фазные напряжения можно рассматривать как ЭДС трех генераторов гармонических колебаний, внутренние сопротивления которых в рабочих режимах значительно меньше их сопротивлений нагрузок, что необходимо для высокого КПД генератора.

Главное свойство симметричных трехфазных систем состоит в том, что сумма напряжений или токов фаз в любой момент времени равна нулю. Это свойство позволяет электрически связывать (соединять) между собой три фазы генератора и нагрузки.

Основное преимущество связанной трехфазной системы перед возможной в принципе не связанной системой с изолированными друг от друга фазами состоит в том, что здесь отпадает необходимость в обратном проводе и можно, в принципе, обходиться тремя проводами вместо шести. Это дает огромную выгоду при больших расстояниях между местами генерирования и потребления энергии.

Различают два вида соединения трехфазных систем: звездой, использующее равенство нулю токов, и треугольником, использующее равенство нулю напряжений.

Соединение фаз генератора и нагрузки в звезду показано на рис.3.23. Это соединение также называют трехфазной четырехпроводной схемой.

При соединении звездой начала фазных обмоток источника соединяют в одну нейтральную точку О, а концы обмоток образуют три вывода А. В, С. Аналогично соединяются три нагрузки, образуя трехфазную нагрузку с нейтралью О'. Нейтрали источника и нагрузки соединяются.

Провода, соединяющие начала фаз обмоток генератора и нагрузки называтся линейными. Провод соединяющий

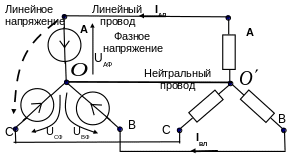
Рис.3.23. Соединение фаз генератора и нагрузки звездой

нейтральные точки генератора и приемника – нейтральным.

Токи в линейных проводах называются линейными, а токи в фазах генератора – фазными токами.

Напряжение между началом и концом каждой фазы (или между линейным и нейтральным проводом) называется фазным напряжением.

Напряжение между началами фаз (или линейными проводами) называется линейным напряжением.

В рассматриваемой схеме фазный и линейный токи равны: . Линейное напряжение между выводами А и В Линейное напряжение связано с фазным следующим соотношением Для силовых сетей низкого напряжения

В симметричном режиме ток через нейтральный провод равен нулю. По этой причине его иногда называют нулевым проводом.

В реальных трехфазных цепях строгая симметрия практически исключена. При несимметрии однофазной нагрузки (к примеру, когда к одной фазе подключили электроприемники от 100 квартир, к другой от 200, а к третьей от 50 квартир) ток в нейтральном проводе отличен от нуля, хотя и значительно меньше линейных токов. В ряде случаев нейтральные точки генератора и нагрузки заземляются, и тогда нейтральным проводом частично или целиком является земля.

Следует помнить, что нейтральный провод обеспечивает постоянство фазного напряжения. При отсутствии нейтрального провода и несимметрии нагрузок фазные напряжения приемников могут стать равными фазным напряжениям генераторов, из-за чего на приемниках могут возникнуть значительные перенапряжения (о случаях обрыва нейтрального провода и массовом выходе из строя бытовых электроприемников - холодильников, телевизоров и пр.- неоднократно писала пресса). Запомните, что ни в коем случае нельзя включать плавкие предохранители в нейтральный провод.

При соединении треугольником все фазные обмотки источника или сопротивления нагрузки соединяются последовательно и в качестве выводов берут общие точки соединений.

В такой схеме (трехфазной трехпроводной) фазные и линейные напряжения равны.

Линейный ток равен разности двух смежных фазных токов. Можно показать, что