3.3.4. Частотные свойства электрической цепи

Все электрические цепи независимо от своего назначения, принципов внутреннего устройства и уровня сложности представляют собой систему, т. е. совокупность физических объектов, между которыми существует определенное взаимодействие. В структуре системы, как отмечалось ранее, можно выделить вход, на который подается исходный электрический сигнал, и выход, на котором возникает полезный сигнал (отклик).

В ряде случаев, чтобы можно было сравнивать и классифицировать электрические цепи, не описывая процессы внутри них, систему представляют в виде «черного ящика» (ящика с неизвестным внутренним содержанием из которого «торчат» четыре провода), для которого интересна и важна лишь связь между сигналами на входе и на выходе.

При таком подходе электрическую цепь характеризуют так называемыми системными функциями, связывающими входное воздействие и отклик цепи на него. Одной из важнейших системных функций четырехполюсной электрической цепи (цепи класса SISO: single inputs – один вход – single outputs –один выход) является комплексный коэффициент передачи. Его используют для оценки отклика цепи на входной гармонический сигнал. Поскольку в этом случае отклик также гармонический, то выходной сигнал будет отличаться от входного лишь амплитудой и начальной фазой.

Комплексный коэффициент передачи двухпортовой четырехполюсной цепи SISO по напряжению это отношение комплексной амплитуды напряжения на выходе цепи на частоте ω к комплексной амплитуде входного гармонического воздействия

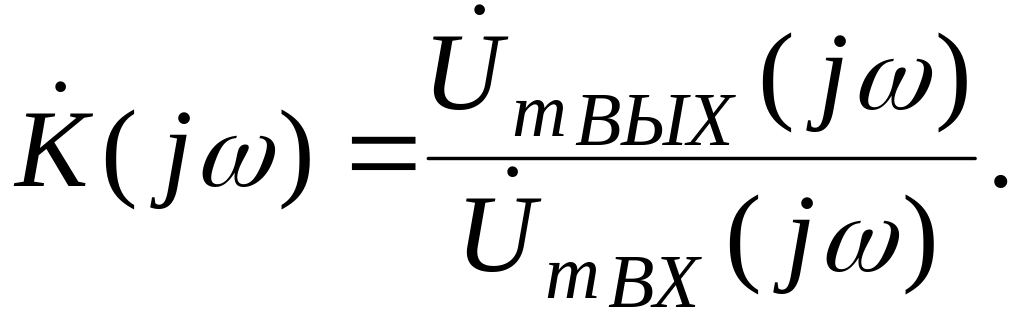(3.48)

При изменении частоты подводимого сигнала коэффициент передачи не остается постоянным. Это происходит потому, что величины сопротивлений элементов цепи, входящих в состав электрической схемы и определяющих коэффициент передачи зависят от частоты

Безразмерная, зависящая от частоты, в общем случае комплекснозначная функция является исчерпывающей характеристикой цепи в частотной области. Для специалистов эта функция относится к числу фундаментальных профессиональных понятий

Функция имеет простую интерпретацию: если на вход цепи поступает гармонический сигнал с известной частотой ω и комплексной амплитудой , то комплексная амплитуда выходного сигнала равна произведению сигнала на входе на коэффициент передачи

(3.49)

Т.е. в сущности, комплексный коэффициент передачи по напряжению , как обобщенная характеристика электрической цепи, описывающая ее свойства, определяет отклик электрической цепи на гармонический сигнал единичной амплитуды и нулевой начальной фазы

Комплексный коэффициент передачи, как отношение двух комплексных величин, сам является комплексной величиной. Поэтому часто удобно представлять его в показательной форме описания комплексных чисел

(3.50)

Модуль комплексного коэффициента передачи называют амплитудно – частотной характеристикой (АЧХ) четырехполюсной цепи. Аргумент комплекснозначной функции φ(ω) называют фазо – частотной характеристикой четырехполюсной цепи.

Следует иметь в виду, что АЧХ и ФЧХ электрической цепи не зависит от амплитуды входного воздействия, а определяются данными самой цепи: числом, характером, номиналами, порядком соединения друг с другом элементов. АЧХ и ФЧХ относительно просто можно получить экспериментально.

АЧХ и ФЧХ являются функциями вещественной частоты и могут быть изображены в виде графиков. Эти функции часто называются кратко частотными характеристиками цепи.

Форма АЧХ позволяет судить о способности электрической цепи либо осуществлять «предпочтительный выбор», «избирательный выбор» сигналов определенного диапазона частот, либо, наоборот, - «блокировать их», «заграждать им путь».

Форма ФЧХ позволяет судить о способности электрической цепи задерживать на время сигналы определенного диапазона, осуществлять их «запаздывание».

При изображении частотных характеристик той или иной электрической цепи обычно строят отдельные графики АЧХ и ФЧХ. Однако кроме указанной пары характеристик, изображаемых в вещественной декартовой системе координат, применяют и так называемую амплитудно-фазовую характеристику, которую строят на комплексной плоскости Z в виде одного графика. Подобная возможность основана на том, что каждому значению частоты соответствует определенное значение в виде некоторого комплексного числа. В комплексной плоскости Z этому комплексному числу соответствует определенная точка плоскости или, что тоже, вектор, соединяющий начало координат плоскости с указанной точкой. С изменением ω конец указанного вектора описывает на комплексной плоскости некоторую кривую. Ее называют годографом комплексного коэффициента передачи по напряжению. Следовательно, амплитудно-фазовая характеристика представляет собой геометрическое место концов векторов, изображающих . Каждая точка этой характеристики, для которой известна частота, дает значения обеих составляющих: модуля и фазы или вещественной и мнимой частей.

Рассмотрим определение АЧХ и ФЧХ для типичных электрических цепей.

Пусть требуется определить для электрической цепи, показанной на рис. 3.15.

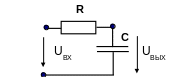
Рис.3.15. Пример 1 для определения АЧХ и ФЧХ электрической цепи

Вычисление комплексного коэффициента передачи по напряжению начинается с того, что производится определение комплексных сопротивлений элементов цепи. Для этого каждому элементу электрической цепи ставится в соответствие его комплексное сопротивление. В нашем случае Z_R =R, Z_C =1/jωC.

Затем, предполагая известной комплексную амплитуду напряжения на входе, находят, пользуясь одним из описанных выше методов, комплексную амплитуду напряжения на выходе четырехполюсника.

Для анализируемой простейшей цепи, представляющей делитель напряжения, удобно воспользоваться правилом простейшего делителя напряжения. Записываем

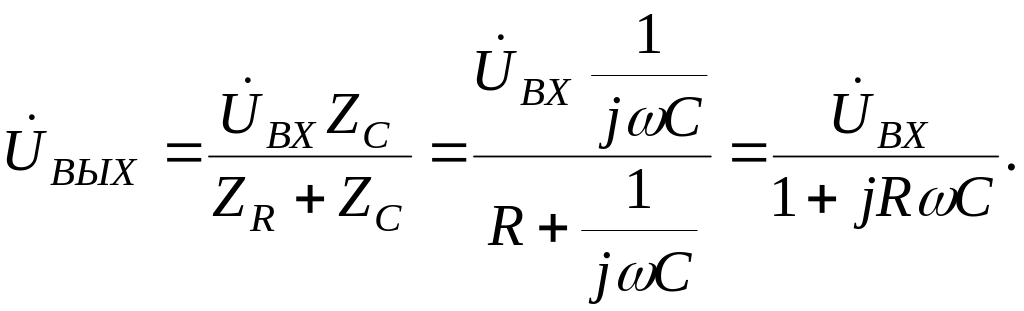(3.51)

Для того, чтобы построенные частотные характеристики имели более общий вид, а не относились только к частным значениям параметров цепи, величины, откладываемые по осям абсцисс и ординат, удобно выражать в относительных единицах, вводя так называемую нормировку. Нормировка частоты состоит в том, что выбирают некоторую базисную частоту ω_С и определяют относительную (безразмерную) нормированную частоту:

(3.52)

Тогда

(3.53)

Вычисляя модуль и аргумент, находим формулы для АЧХ и ФЧХ

АЧХ (3.54)

ФЧХ (3.55)

Графики АЧХ и ФЧХ, построенные по полученным соотношениям показаны на рис3.16.

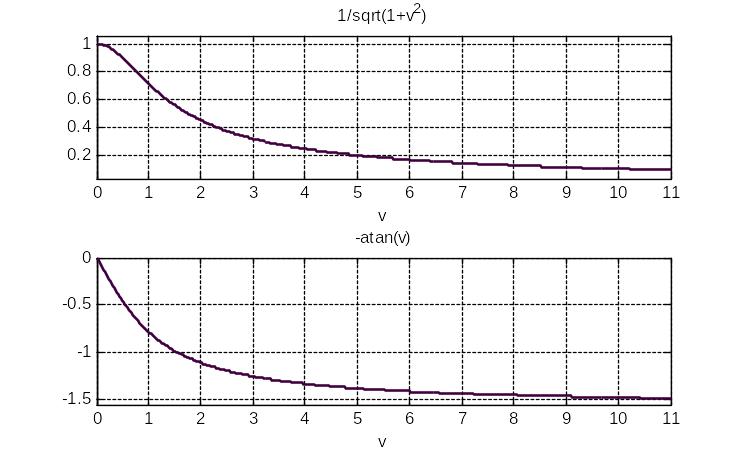
Рис.3.16. Графики АЧХ и ФЧХ цепи, показанной на рис.3.15

Показанные на рис АЧХ и ФЧХ позволяют наглядно судить о том, какие частотные составляющие доминируют на выходе цепи и какие, наоборот, ослабляются.

На низких частотах выходное напряжение приблизительно равно входному, а с ростом частоты выходное напряжение уменьшается до нуля. Такая электрическая цепь по понятным причинам называется фильтром низких частот: она пропускает (выделяет из всей совокупности сигналов) сигналы низких частот и «подавляет» сигналы высоких частот. На практике ее используют очень широко, например, для удаления высокочастотных сигналов (пульсаций) на выходе источников питания, вырабатывающих постоянное напряжение.

В анализируемой простейшей схеме, показанной на рис.3.15, частотные свойства цепи можно было предсказать, опираясь на свойства РЭ и ЕЭ. Действительно, при небольших частотах сигнала конденсатор из – за блокирующего свойства ЕЭ представляет собой разрыв цепи. Если его исключить из цепи, то становиться очевидным, что на низких частотах вход и выход оказываются соединенными и вполне естественно, что все входное напряжение прикладывается на выход. На высоких частотах конденсатор, из – за шунтирующего свойства ЕЭ, представляет КЗ перемычку, подключенную параллельно выходу. Понятно, что при этом выходное напряжение будет равно нулю.

При ω = 0 K(ω) = 1.

При ω = ∞ K(ω) = 0.

При K(ω) = 1.

Аналогичными свойствами обладает электрическая цепь, показанная на рис.3.17.

Рис.3.17. Пример 2 для определения АЧХ и ФЧХ электрической цепи

Аналогично, как это было сделано ранее (только теперь ω_L =R/L), можно получить АЧХ и ФЧХ для этой цепи. Графики АЧХ совпадают с ранее рассмотренным, поэтому эта цепь также представляет собой фильтр низких частот. Благодаря блокирующему действию ИЭ высокочастотные сигналы не проходят на выход.

Заметим, что предназначение обеих схем совпадает, однако, вообще говоря, чаще используют RC-фильтры. Это связано с тем, что выполняемые намоткой индуктивности более громоздки. Исключение из общей рекомендации составляет один особый случай, весьма распространенный на практике. Так называемые «бусинки» (маленькие ферритовые торроидальные сердечники) нанизываются на провод, из – за чего такое соединение становиться индуктивным. Благодаря блокирующему свойству ИЭ, высокочастотные помехи из силовой промышленной сети не проникают на вход, например, источника питания и, наоборот, не вносят свои импульсные помехи в электрическую сеть.

ФЧХ анализируемых цепей различаются знаком. В RC-фильтре на высоких частотах сигнал подавляет емкость, поэтому сдвиг фаз между входным и выходным сигналом равен примерно –π/2. В RL- цепи высокочастотный сигнал блокирует индуктивность, поэтому фазовый сдвиг между входным и выходным напряжением есть величина положительная и равная примерно π/2.

Мы рассмотрели цепи, представляющие некие фильтры низких частот. Они имели в АЧХ область частот, в пределах которой цепь пропускала сигналы с минимальным ослаблением. Обычно эту область частот называют полосой пропускания. Была в АЧХ и область частот с противоположными свойствами. Область частот, в пределах которой электрическая цепь не пропускает колебания или, по - другому, пропускает с максимальным ослаблением, называется полосой задерживания (запирания, затухания). В зависимости от взаимного расположения областей прозрачности и запирания в электротехнике различают, помимо фильтров низких частот, фильтры верхних частот, полосовые и заграждающие (режекторные).

Частота ω₁ разделяющая полосы прозрачности и запирания, называется граничной частотой или частотой среза.

В некоторых цепях, у которых амплитуды и частоты характеристик изменяются в очень широких пределах, удобно применять логарифмический масштаб. Для этого амплитудно - частотную характеристику по оси ординат выражают в логарифмических единицах децибелах dB: По горизонтальной оси абсцисс в логарифмических АЧХ и ФЧХ частоты откладывают в логарифмических единицах декадах: f_dec =log₁₀f. В этом случае равные расстояния соответствуют равным отношениям величин. АЧХ и ФЧХ, построенным в логарифмическом масштабе (ЛАЧХ и ЛФЧХ), часто приписывают имя Г. Боде и называют диаграммами Боде.