3.2.3. Смешанное соединение элементов цепи

Смешанным называют соединение, образованное параллельным или последовательным соединением участков цепи, в пределах которых отдельные элементы, в свою очередь, соединены только последовательно или параллельно.

Типичным примером такого соединения является схема двухполюсника, показанная на рис.3.6.

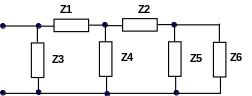
Рис.3.6. Пример смешанного соединения элементов цепи

На этой схеме имеется группа элементов Z₅, Z₆, соединенных параллельно. Эта группа с элементом Z₂ соединена последовательно. Отмеченное последовательно-параллельное соединение, в свою очередь, является участком цепи, включенным параллельно элементу Z₄. Эта группа элементов включена последовательно с элементом Z₁. Наконец, отмеченная выше цепь включена последовательно с элементом Z₂.

Словесная формулировка имеющихся разновидностей соединения выделенных групп последовательных и параллельных элементов называется формулой соединения. Зная формулу соединения можно существенно упростить электрическую цепь, заменив ее эквивалентным двухполюсником с комплексным сопротивлением Z_экв.

Формула смешанного соединения элементов электрической цепи, показанной на рис.3.6 следующая.

Электрическая цепь представляет собой параллельное соединение двух ветвей. В первую ветвь входит элемент с комплексным сопротивлением Z₃. Вторая ветвь образована последовательным соединением элемента Z₁. и параллельно включенных элемента Z₄ и ветви, которая образованна последовательным соединением элемента Z₂. и участка цепи с параллельным соединением элементов Z₅, Z₆.

На основании соотношений по формуле соединения можем записать

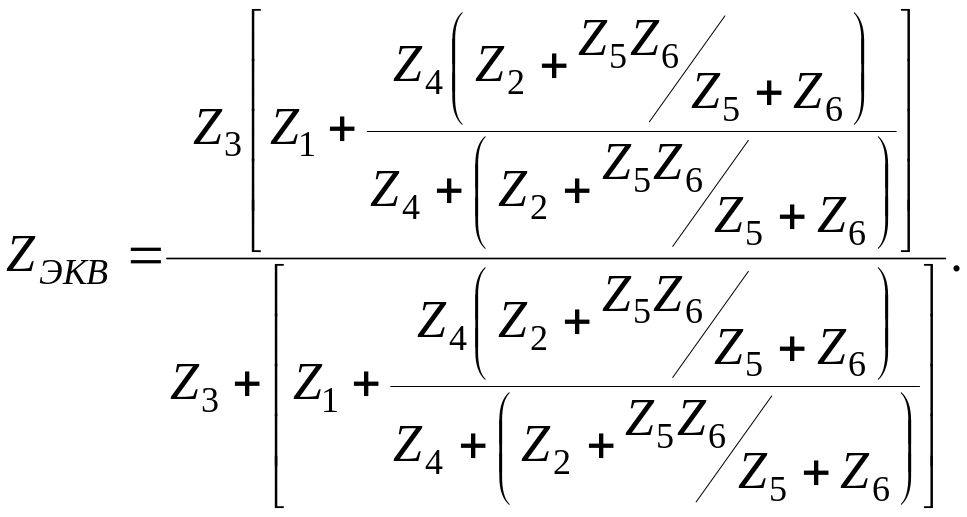(3.18)

3.2.4. Соединение элементов цепи «звездой» и «треугольником»

В ряде случаев не удается осуществить преобразование некоторой части цепи, опираясь на схемы последовательного и параллельного соединения элементов. Для упрощения не представляющих собой смешанное соединение электрических цепей, в электротехнике используют соединения элементов цепи «треугольником» и «звездой» (рис3.7).

Преобразования конфигурации цепи в эквивалентное соединение осуществляются таким образом, чтобы после преобразования режимы остальной, не преобразованной части цепи оставались неизменными. При равенстве комплексных амплитуд токов и напряжений между соответствующими парами полюсов (выводов) в исходной и преобразованной цепях будут равны и комплексные сопротивления обоих трехполюсников между рассматриваемыми парами полюсов.

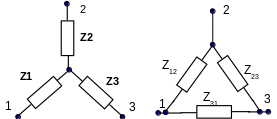
Рис.3.7. Пример соединения элементов цепи «звездой» и «треугольником»

Опираясь на это условие эквивалентности, без вывода запишем формулы, позволяющие рассчитывать комплексные сопротивления одного типа соединения по известным величинам сопротивлений другого.

Если заданы комплексные сопротивления «треугольника» и отыскиваются сопротивления эквивалентной ему «звезды», то следует пользоваться формулами:

(3.19) (3.20)

(3.21)

Правило преобразования «треугольника» в «звезду»: комплексное сопротивление луча «звезды» равно произведению двух комплексных сопротивлений «треугольника», присоединенных в нем к одноименному (подобному) узлу, деленному на сумму всех сопротивлений «треугольника».

Если заданы комплексные сопротивления «звезды» и отыскиваются сопротивления эквивалентного ему «треугольника», то следует пользоваться формулами:

(3.22)

Правило преобразования «звезды» в «треугольник»: комплексное сопротивление ветви треугольника равно сумме попарных произведений комплексных сопротивлений лучей звезды, деленной на комплексное сопротивление луча, не подсоединенного к одноименным узлам.