3.2.2. Параллельное соединение элементов цепи

Параллельным называют такое соединение фрагментов (участков) цепи или отдельных ее элементов, в котором напряжение на всех участках цепи или элементах одинаково по величине и направлению.

Представим параллельное соединение элементов цепи в виде эквивалентного двухполюсника. Схема параллельного соединения трех элементов. подсоединенных к двум узлам, и эквивалентный двухполюсник, которым мы хотим заменить цепь, показаны на рис.3.2.

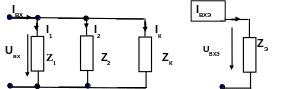
Рис.3.4. Параллельное соединение элементов цепи

Для гармонического сигнала на основании первого закона Кирхгофа имеем

(3.9)

или в общем случае

(3.10)

Напряжение и ток на выводах эквивалентного двухполюсника, которым мы хотим заменить цепь, связаны Законом Ома

(3.11)

Сравнивая (3.10) и (3.11) находим

(3.12)

То есть, комплексная проводимость параллельного соединения элементов электрической цепи равна сумме комплексных проводимостей всех элементов, образующих соединение.

Комплексное сопротивление двух параллельно соединенных элементов определяется следующей формулой

(3.13)

То есть, комплексное сопротивление двух параллельно соединенных элементов электрической цепи равно произведению комплексных сопротивлений этих элементов, деленному на сумму их комплексных сопротивлений

Из (3.9) несложно заметить, что параллельное соединение «делит» входной ток между элементами цепи.

Два параллельно соединенных элемента образуют простейший делитель тока (рис.3.5). Он состоит из двух ветвей.

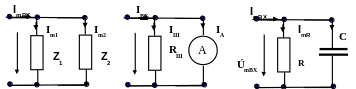
Рис.3.5. Простейший делитель тока и его реализация в приборах измерения тока и для шунтирования резистора

Амплитуды токов в ветвях простейшего делителя соответственно равны

(3.14)

(3.15)

Соотношения (3.14) и (3.15) определяют следующее важное свойство простейшего делителя тока, которое следует запомнить: аплитуда тока в интересующей нас ветви делителя определяется амплитудой входного тока, умноженной на сопротивление другой ветви и деленной на сумму сопротивлений ветвей делителя.

Это свойство свидетельствует о том, что большая часть тока всегда протекает по той ветви сопротивление которой меньше. В частности, если одна ветвь представляет собой КЗ перемычку, то по ней протекает весь ток.

Если требуется уменьшить ток в элементе электрической цепи, то параллельно ему включается элемент, который называется шунтом.

Шунтом принято называть одну из двух параллельно соединенных ветвей, которая подключается для уменьшения тока в другой ветви.

Шунт применяют для расширения пределов измерения тока амперметрами (рис.3.5). Параллельно амперметру с сопротивлением R_A включают специальный резистор с малым сопротивлением R_ш. . В этом случае амперметр вместо реально протекающего тока I_ВХ будет показывать ток

. (3.16)

Делитель тока используют часто в электронике для шунтирования конденсатором резистора по переменному току (рис.3.5).

(3.17)

Представим такие цепочки из формул.

Постоянный ток .

Следовательно, весь постоянный ток протекает через резистор.

Переменный ток высокой частоты

Т.е. в этом случае переменный ток высокой частоты через резистор не протекает.