4. Розрахунок елементів сталевих конструкцій при дії поздовжньої сили зі згином

Перевірка міцності позацентрово навантаженого елемента при виконанні умов, викладених у пункті 10.1 [1], виконується в пружно-пластичній стадії:

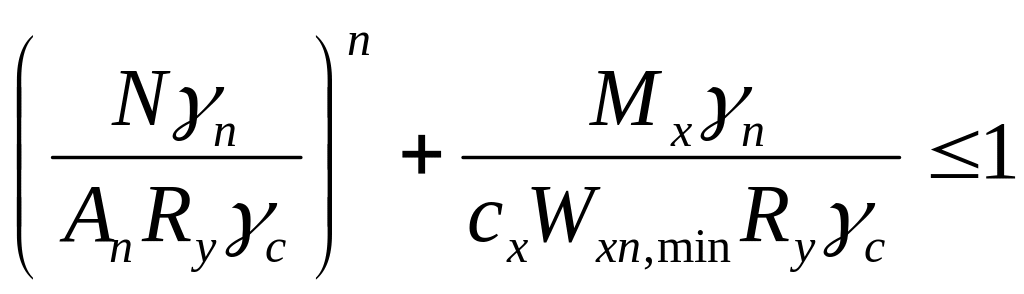. (10.1)

В інших випадках проводиться перевірка в пружній стадії роботи сталі за формулою:

. (10.3)

Стійкість у площині дії згинального моменту перевіряється за формулою:

, (10.6)

а із площини дії моменту за згинально-крутильною формою втрати стійкості – за формулою:

. (10.8)

Позначення величин, що входять у ці формули, а також методика їх визначення наведені в пунктах 10.1.1, 10.2.2 і 10.2.4 [1].

Задача 4.1. Перевірка міцності позацентрово навантаженого стержня

Виконати перевірку міцності стержня із прокатного двотавра З0К2 при дії статичного навантаження, що викликає значення стискаючої поздовжньої сили і згинального моменту в площині стінки . Матеріал стержня – сталь С235, коефіцієнт надійності за призначенням , коефіцієнт умов роботи , дотичні напруження не перевищують .

Розв’язання

1. Із сортаменту (табл. Б.5) вибираємо необхідні розміри і геометричні характеристики перерізу двотавра З0К2: ; ; ; .

2. За табл. Г.2 [1] (табл. А.2) визначаємо розрахунковий опір фасонного прокату товщиною зі сталі С235: ; і характеристичне значення межі текучості: .

3. Перевіряємо умови, викладені в пункті 10.1.1 [1]:

;

– дано в умові задачі;

.

Оскільки всі умови задовольняються, для перевірки варто скористатися формулою (10.1).

4. Визначаємо співвідношення площ полиці і стінки двотавра, що перевіряється:

.

З урахуванням цієї величини за табл. М.1 [1] (табл. А.2) для перерізу типу       визначаємо коефіцієнти: , .

5. Виконуємо перевірку міцності за формулою (10.1):

.

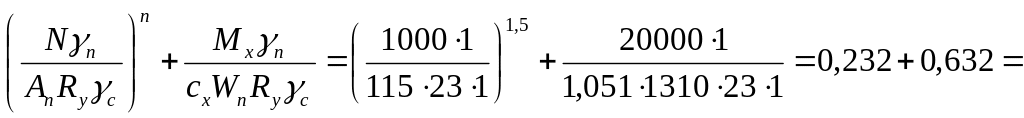
Отже, міцність перевіреного стержня забезпечена.

Задача. 4.2. Перевірка стійкості позацентрово стиснутого стержня в площині дії моменту

Виконати перевірку стійкості в площині дії моменту позацентрово стиснутого стержня з двотавра 40Ш2, що згинається в площині стінки. Розрахункова довжина стержня дорівнює 18,8 м, розрахункові зусилля і , сталь – С285, коефіцієнт надійності за призначенням , коефіцієнт умов роботи .

Розв’язання

1. Виписуємо із сортаменту (табл. Б.5) необхідні розміри і геометричні характеристики перерізу двотавра 40Ш2: ; ; ; , .

2. За табл. Г.2 [1] (табл. А.2) визначаємо розрахунковий опір фасонного прокату товщиною зі сталі С285: .

3. За формулою з пункту 4.2 [1] обчислюємо умовну гнучкість у площині згину:

.

4. За формулою з пункту 10.2.2 [1] обчислюємо відносний ексцентриситет навантаження:

.

5. Обчислюємо відношення площі полиці до площі стінки для перерізу двотавра 40Ш2:

.

6. Із табл. К.2 [1] для перерізу типу 5 визначаємо значення коефіцієнта форми перерізу:

.

7. Обчислюємо приведений відносний ексцентриситет за формулою (1.6.6) [1]:

.

8. Лінійною інтерполяцією за табл. Ж.3 (табл. А.6), виходячи з приведеного відносного ексцентриситету й умовної гнучкості , визначаємо значення коефіцієнта стійкості при позацентровому стиску: .

9. Виконуємо перевірку стійкості в площині дії згинального моменту за формулою (10.6) [1]:

.

Перевірений стержень нестійкий у площині дії згинального моменту.

Задача 4.3. Перевірка стійкості позацентрово стиснутого стержня з площини дії моменту

Виконати перевірку стійкості з площини дії згинального моменту позацентрово стиснутого стержня з двотавра 35Б2, що згинається в площині стінки, при шарнірному обпиранні по кінцях. Розрахункова поздовжня сила , максимальний згинальний момент у межах середньої третини довжини . Розрахункова довжина з площини згину . Матеріал стержня – сталь С245, коефіцієнт надійності за призначенням , коефіцієнт умов роботи .

Розв’язання

1. Виписуємо із сортаменту (табл. Б.5) необхідні розміри і геометричні характеристики перерізу двотавра 35Б2: ; ; ; ; ; .

2. За табл. Г.2 [1] (табл. А.2) визначаємо розрахунковий опір фасонного прокату товщиною зі сталі С245: .

3. За формулами з пункту 4.2 [1] визначаємо гнучкість і умовну гнучкість стержня із площини згину:

; .

4. За табл. 8.1 [1] (табл. А.4) визначаємо тип кривої стійкості. Для прокатного двотавра приймаємо тип b.

5. Лінійною інтерполяцією за табл. Ж.1 [1] (табл. А.5) залежно від отриманого значення умовної гнучкості обчислюємо значення коефіцієнта стійкості при центральному стиску відносно осі :

.

6. За формулою з пункту 10.2.2 [1] обчислюємо відносний ексцентриситет навантаження в площині згину:

.

7. Коефіцієнт , що враховує вплив ексцентриситету навантаження, визначається за пунктом 10.2.5 [1]. Для цього обчислюються допоміжні коефіцієнти за вказівками табл. 10.2 [1]. Для симетричного двотаврового перерізу й отриманого вище значення відносного ексцентриситету коефіцієнт обчислюється за формулою:

.

8. Для обчислення коефіцієнта необхідно знати значення гнучкості . Оскільки , з табл. Ж.1 [1] (табл. А.5) визначаємо при коефіцієнт . Відповідно до табл. 10.2 [1], коефіцієнт дорівнює:

.

9. За табл. 10.2 обчислюємо коефіцієнт :

.

10. З урахуванням отриманих допоміжних величин обчислюємо коефіцієнт за формулою (10.9) [1], оскільки вище отримано :

.

11. Виконуємо перевірку стійкості з площини дії згинального моменту за формулою (10.8) [1]:

.

Стержень, що перевіряється, задовольняє вимоги стійкості з площини дії згинального моменту.