Индивидуальные задания

В вариантах 1-10 решить неравенства:

Вариант 1.

;
;	;
;

Вариант 2.

Вариант 3.

Вариант 4.

Вариант 5.

Вариант 6.

Вариант 7.

Вариант 8.

;

Вариант 9.

Вариант 10.

Задачи с параметрами

Пример 1. Найти все значения параметра а, для которых уравнение

имеет решения.

Решение. Отметим, что (при этом значении параметра знаменатель дроби обращается в нуль). Так как , то потребуем, чтобы

Решая это неравенство, получаем, что .

Ответ: .

Пример 2. Решить уравнение: .

Решение. Учитывая, что , а , имеем

,

.

Данное уравнение равносильно совокупности уравнений

Первое уравнение совокупности имеет решение . Второе уравнение сводится к квадратному относительно :

.

Обозначим . Тогда уравнение принимает вид

.

При , т.е. при 4а + 5 < 0, , уравнение не имеет действительных решений.

В случае ,т.е. при 4a+5 = 0, , получаем и .

Если , т.е. при 4а+5 > 0, ,рассматриваемое уравнение имеет два различных действительных решения. Выясним, при каких значениях параметра a хотя бы одно из решений удовлетворяет условию . Из уравнения получаем, что

.

Рассмотрим ограничения на каждый полученный корень уравнения

отдельно.

а) Пусть . Тогда потребуем, чтобы

; ;

; (при ).

Отсюда ; .

б) Пусть . Тогда

; ;

; ;

; .

Отсюда получаем, что при , при , .

Возвращаясь теперь к переменной х, запишем окончательный ответ

при , ;

при , , ;

при

;

при

при .

Пример 3. При каких значениях параметра р уравнение имеет решения?

Решение. Отметим, что уравнение может иметь решения при . Преобразуем левую часть уравнения к виду

.

Тогда имеем

.

Так как , то получаем ограничения на правую часть данного уравнения:

,

.

При обе части неравенства принимают только положительные значения, поэтому перейдем к равносильному неравенству

,

,

,

.

Отсюда . С учетом ограничений на р получаем ответ.

Ответ: .

Пример 4. Найти все значения параметра а, при которых уравнение имеет на отрезке ровно три корня.

Решение. Уравнение легко сводится к квадратному относительно sin x:

,

решая которое, получаем равносильную совокупность уравнений

Уравнение на отрезке имеет два решения , .

Поэтому уравнение должно иметь на этом отрезке только одно решение х₃ (рис. 8). Это возможно лишь при , когда а =1.

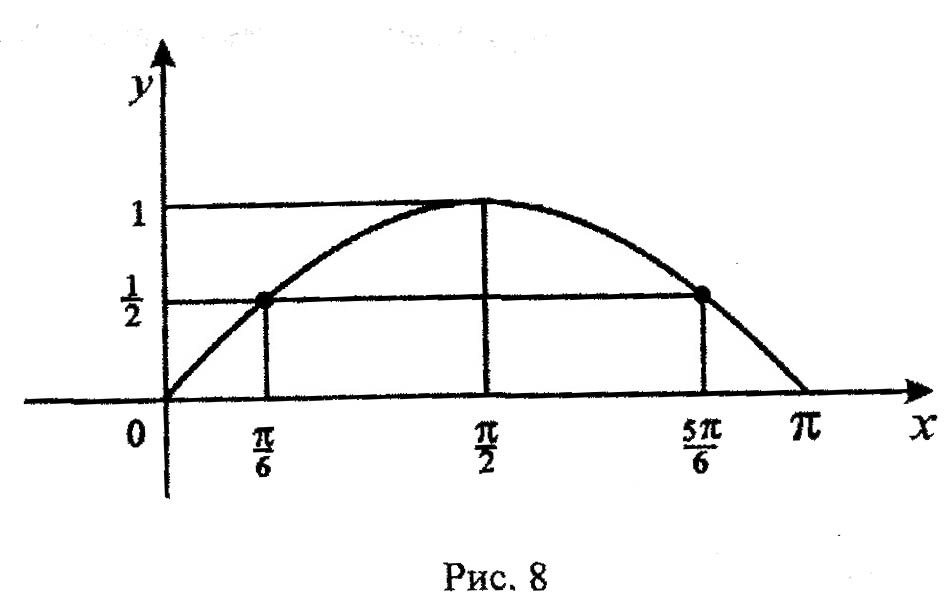
Ответ: a=1.

Пример 5. Найти все значения параметра а из интервала (2; 5), при

каждом из которых существует хотя бы одно число х из отрезка [2; 3], удовлетворяющие уравнению .

Решение. Оценим обе части уравнения. Так как , , то получаем очевидные неравенства

,

,

.

Следовательно, исходное уравнение равносильно системе уравнений вида

Тогда при п = 1, . Найдем, при каких а выполняется равенство .

Имеем . C учетом того, что по условию задачи , записываем неравенство на :

,

Отсюда и .

Ответ: .

Пример 6. Найти значения параметра а, при которых квадратный трехчлен имеет только два

одинаковых по абсолютной величине корня разных знаков.

Решение. Уравнение имеет смысл при . Из условия задачи , поэтому по теореме Виета и . Получаем, что , при условии, что .

.

Так как , то

,

.

С учетом условия , имеем

и

Ответ: .

Пример 7. При каких значениях параметра а уравнения и sin3x равносильны?

Решение. Первое уравнение равносильно совокупности уравнений

Так как второе уравнение можно преобразовать к виду ,

то оно также равносильно совокупности уравнений вида

Потребуем, чтобы являлось решение уравнения

. Получаем, что при этом .

Тогда и уравнение запишется в виде

.

Данное уравнение равносильно совокупности уравнений

при условии, что .

Таким образом, при , и исходные уравнения равносильны.

Ответ: , , .