2. Кинематический расчёт узла

4.2.2.1 Выбор структуры привода Определяется общий диапазон регулирования привода

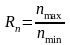(1)

где n_max – наибольшая частота вращения шпинделя, мин ^–1;

n_min – наименьшая частота вращения шпинделя, мин ^–1.

Определяется знаменатель геометрического ряда φ по формуле:

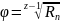, (2)

где z – количество ступеней частот вращения.

Принимается стандартное значение знаменателя φ. Значение φ=1,06 практически не используется, φ=1,12 применяют преимущественно в станках с программным управлением и в тяжёлых станках. Наибольшее распространение получили значения φ=1,26, φ=1,41, φ=1,58, φ=1,78 применяют в специализированных станках; φ=2 практически не используют.

Исходя из принятого стандартного значения φ определяется ряд стандартных частот вращения коробки скоростей (табл.4.3 [1]).

Далее для заданного числа z составляют структурные формулы. Если частоты вращения шпинделя изменяются по геометрическому ряду, то передаточные отношения передач в группах образуют геометрический ряд со знаменателем ^х, где х – целое число, называемое характеристикой группы передач. Для последовательного получения частот вращения шпинделя сначала переключают передачи одной группы, затем другой и т. д. В зависимости от принятого порядка переключений группа может быть:

- основной, характеристика, которой определяется по формуле:

х₀ = 1 (3)

- первой переборной группой, для которой характеристика определяется по формуле:

х₁ = р₁ (4)

где р₁– число передач в основной группе;

- второй переборной группой, для которой характеристика определяется по формуле:

х₂ = р₁ р₂ (5)

где р₂– число передач в первой переборной группе.

Основной и различными по номеру переборными группами может быть любая группа передач в приводе.

Для каждой структурной формулы строят структурную сетку. В них находит отражение относительная связь между передаточными отношениями в группах, поэтому лучи для каждой группы проводятся симметрично, а количество интервалов между их концами численно равно характеристике группы, определяемой в соответствии со структурной формулой.

Пример построения структурных сеток для структурных формул z = 6 = 3(1)·2(3); z = 6 = 3(2)·2(1)

Если изменить порядок следования групп (сначала двойной блок, потом тройной), получим: z = 6 = 2(1)·3(2); z = 6 = 2(3)·3(1)

Порядок построения СТС:

1) На равных расстояниях проводят столько горизонтальных линий, сколько скоростей имеет привод;

2) На равных расстояниях проводят вертикальные линии на одну больше, чем число групп передач. Поле между двумя вертикальными линиями отводится для одной группы передач. Проставляются римскими цифрами номера валов (они могут идти не по порядку), на СТС нет постоянных передач;

3) Над СТС над соответствующим полем в порядке конструктивного расположения групп в приводе указывают число передач в группе Р_i и ее характеристику X_i;

4) На середине первой левой вертикали намечают точку О, из которой симметрично горизонтали проводят лучи в количестве, равном Р_i, и с расстоянием между концами лучей на следующей вертикали, равным Х_i;

5) Из каждой полученной точки на второй и последующих вертикалях аналогичным путем проводят лучи для второй, третьей и т.д. групп передач.

Пример: z = 6 = 2(3)·3(1)

Рисунок 1 – Структурная сетка

Выбор оптимальной структурной сетки:

1) Диапазон регулирования последней переборной группы должен быть наибольшим (φ = 1,26; Х_max = 9). Поэтому исключить из рассмотрения варианты, не удовлетворяющие этому условию (стр.59 [1]).

2) С уменьшением частоты вращения вала при постоянной мощности крутящий момент увеличивается, а значит и увеличиваются размеры деталей передач привода («веерообразность»);

3) В качестве последней переборной группы выбирают группу с наименьшим числом передач;

4) Характеристики групп должны увеличиваться от эл. двигателя к шпинделю.