Телеологические траектории

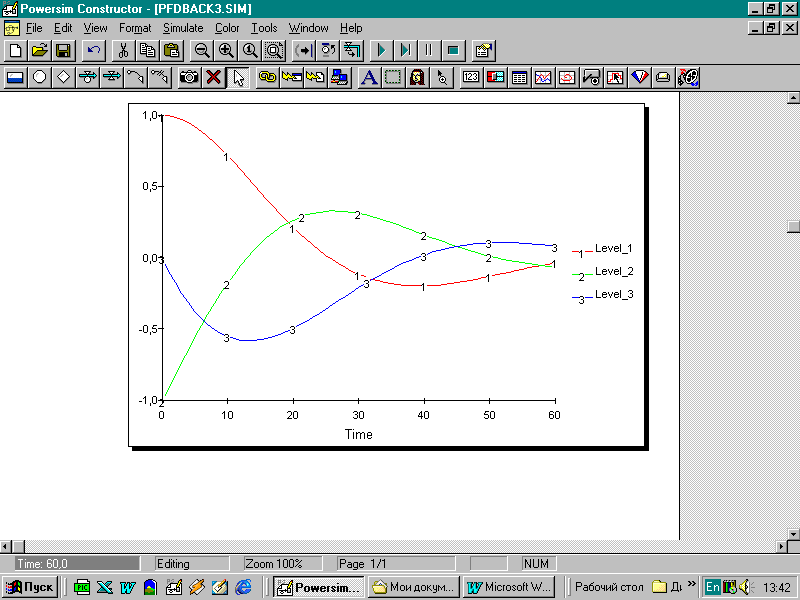
Третье отдельное семейство – это семейство телеологических траекторий (рис. 11).

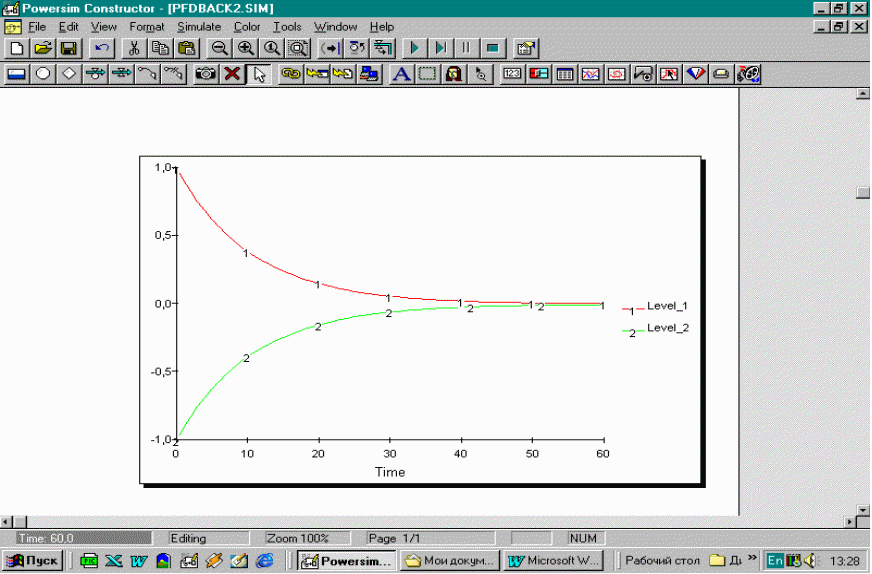
Рисунок 11 – Семейство телеологических траекторий

Все живые системы (и многие неживые) проявляют телеологическое поведение. Этот тип поведения связан с экспоненциальным упадком, что видно, если сравнить временную траекторию на рисунке 10 б с верхней траекторией на рисунке 11, где целевым уровнем является нулевой.

Такое поведение возникает при наличии отрицательной петли обратной связи. Состояние сравнивается с целью – если есть расхождения между желательным и актуальным состоянием, предпринимается корректирующее воздействие, чтобы выровнять систему, приблизив её к целевому состоянию. Когда вы голодны, вы едите, чтобы утолить голод. Если вы устали, вы спите, чтобы восстановить энергию и бодрость. Когда запас готовой продукции фирмы падает ниже количества, необходимого для обеспечения нормального обслуживания клиентов и темпа реализации, производство наращивается, пока запас не станет достаточным.

Иногда желаемое состояние и корректирующее воздействие являются явными и находятся под контролем лица, принимающего решение, как в примере со страховым уровнем запаса. Иногда цель неявная, и её достижение находится вне сознательного контроля: например, количество сна, необходимого, чтобы почувствовать себя хорошо отдохнувшим – фактор физиологический.

Темп приближения к целевому состоянию системы уменьшается по мере уменьшения рассогласования между ними. Когда соотношение между величиной рассогласования и корректирующей поправкой линейно, темп поправки точно пропорционален величине рассогласования, и результирующее телеологическое поведение эквивалентно экспоненциальному упадку.

Колебательные траектории

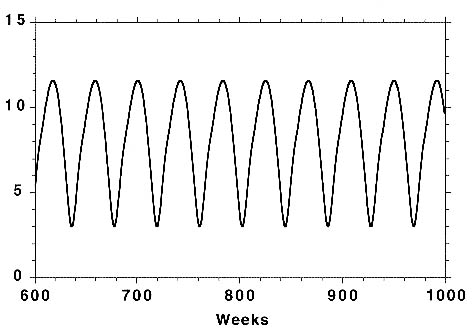
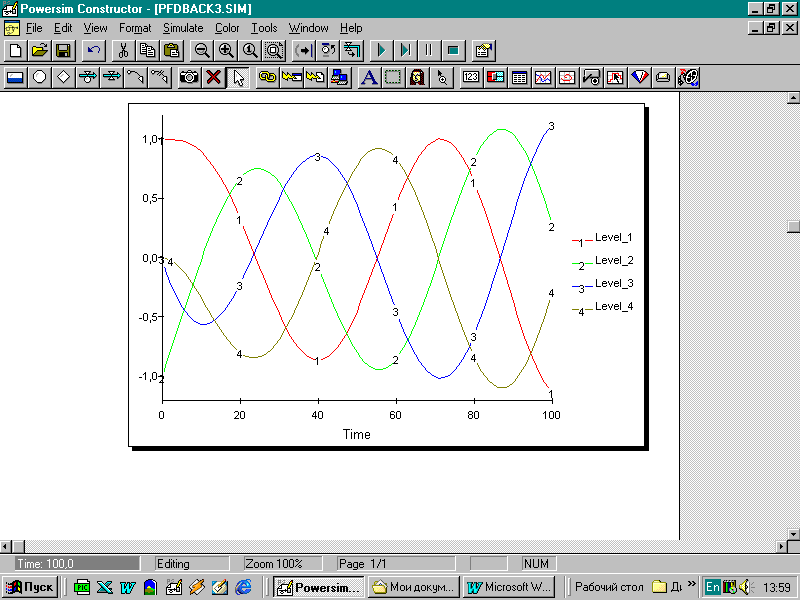
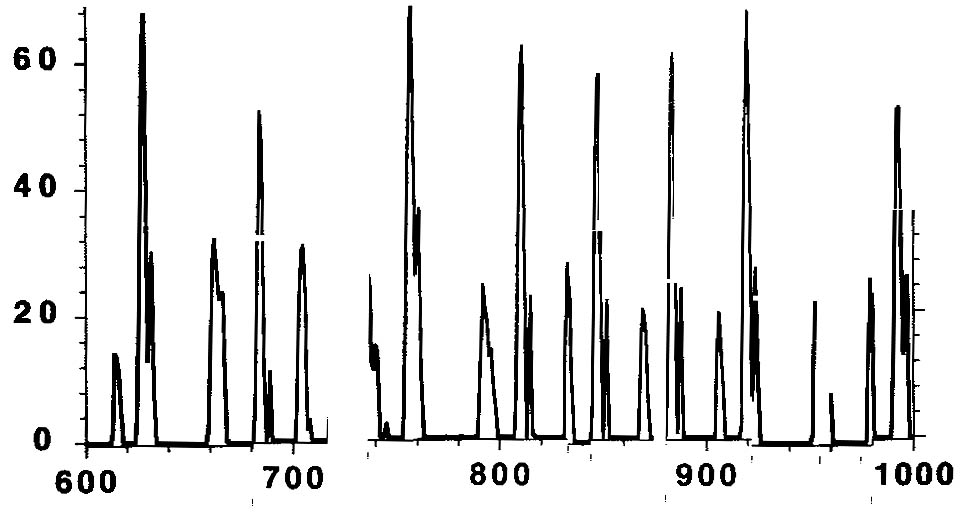
Четвертое отдельное семейство – это семейство колебательных траекторий. Колебание – одно из самых распространенных типов динамического поведения и характеризуется различными прототипами. Основные типы: устойчивые колебания (рис. 12 а), затухающие колебания (рис. 12 б), расходящиеся колебания (рис. 12 в), хаотические колебания (рис. 12 г). Каждое из них обусловлено соответствующей структурой обратной связи и набором параметров, определяющих силу цепей обратных связей и продолжительность задержек в них.

В основе любого из колебательных типов траекторий – отрицательная петля обратной связи с задержками. Осцилляции возникают в случае существенной задержки в любой части информационной обратной связи: понимание состояния обусловлено временем, необходимым для измерений и документирования отчета; могут быть задержки в инициации корректирующего действия, т. к. нужно время на принятие решения; само корректирующее действие с запаздыванием влияет на изменение состояния системы.

а	б
в	г

Рисунок 12 – Семейство колебательных траекторий

Затухающие осцилляции демонстрируют системы, в которых протекают диссипативные и релаксационные процессы. Примеры таких процессов включают трение в физических системах и информационное сглаживание в социальных системах.

Взрывные осцилляции либо возрастают до перехода в устойчивый режим колебаний либо возрастают, пока это не приведет к разрыву системы (коллапсу). В результате, взрывные осцилляции обычно не часто встречаются в реальном мире, а если и случаются, то не продолжаются слишком долго.

Хаотическое поведение – это осциллирующая временная траектория, которая разворачивается нерегулярно и никогда не повторяется (т. е. её период по существу бесконечен). Хаос – уникальный тип временной траектории, т. к. это по существу случайное поведение, генерируемое системой, свободной от случайности.

Три базовые модели поведения – экспоненциальная, телеологическая и колебательная – продуцируются тремя базовыми структурами обратной связи: положительной обратной связью, отрицательной обратной связью и отрицательной обратной связью с задержками.

Другие, более сложные модели поведения, являются следствием нелинейного взаимодействия этих базовых системно-динамических структур друг с другом.

S-образные траектории

Пристальное изучение модели S-образного роста (рис. 13 а) показывает, что на самом деле это комбинация двух временных моделей поведения – экспоненциального роста и телеологического поведения. Точнее, в случае S-образного роста экспоненциальный рост уступает место телеологическому поведению по мере приближения системы к пределу или несущей способности (отмеченной прямой линией).

а	б
в	г

Рисунок 13 – Семейство S-образных траекторий

Система демонстрирует S-образный рост только при наличии двух критических условий. Во-первых, петли отрицательных обратных связей не должны содержать существенных временных задержек (если они есть, популяция перекрывает несущую способность и начинает колебаться вокруг нее – рис. 13 г). Во-вторых, несущая способность должна быть постоянной, т. е. не должна «потребляться» популяцией.

Главный аспект типовой структуры, генерирующей S-образный рост, – нелинейное взаимодействие положительных и отрицательных петель обратной связи. Вначале, когда состояние системы слабо зависит от ресурсной базы, доминируют положительные петли. По мере приближения к пределам роста начинают доминировать отрицательные петли. Точка перегиба S-образной кривой является точкой, в которой система, продолжая расти, смещается от акселерации к торможению. Эта же точка знаменует сдвиг в доминировании петель обратной связи.

Временные задержки в отрицательных петлях обратной связи обусловливают возможность превышения и колебаний вокруг линии несущей способности при условии, что она не разрушается (рис. 13 г). С другой стороны, если система перекрывает несущую способность, и несущая способность разрушена, систему ожидает коллапс (рис. 13 в). Это называют реакцией системы в виде «перегрузки и коллапса».

Третьим возможным выходом из ситуации перегрузки является то, что система просто изменит направление и приблизится к траектории системной мощности в перевернутой S-образной модели (рис. 13 б). Как и в случае с «нормальной» S-образной моделью, перевернутая S-образная модель является комбинацией двух временных траекторий – экспоненциального упадка и самоусиливающегося упадка.