6.2.3. Перетворювачі кодів для стискання і розгортання інформації

Обмін інформацією між людиною та ЕОМ, а також між різними пристроями останньої дуже часто супроводжується зміною форми зображення цієї інформації, або, інакше кажучи, перетворюванням кодів даних.

У системі, зображеній на рис.6.2, введені з клавіатури десяткові цифри шифратор перетворює в чотирирозрядний двійковий код, який і обробляє процесор, а результат обробки дешифратор перетворює з чотирирозрядного двійкового коду в семисегментний, який вихідні індикатори перетворюють у десяткові числа. Під час перетворення десяткових чисел у двійкові дані стискуються, оскільки десятирозрядний код "1 з 10" перетворюється в чотирирозрядний двійковий код 8-4-2-1. Із стисканням даних пов'язане поняття шифрування, а з розгортанням - дешифрування.

Дешифратором називають комбінаційну схему з кількома входами й виходами, яка перетворює код, поданий на входи, в сигнал на одному з виходів.

Двійкові дешифратори перетворюють двійковий код у код "1 з N". Якщо на n входів такого дешифратора подано двійкові змінні, то на одному з 2ⁿ виходів виробляється сигнал 1, а на решті зберігається сигнал 0. Дешифратор, який мав N=2ⁿ виходів, називають повним. Коли частини вхідних кодів не використано, то N<2ⁿ і дешифратор неповний.

Т₂

Т₂

Т₂

3

х

9

1

Т₁

Т₁

х

1

1

х

Т₁

х

х

7

5

х

х

х

х

1

х

х

6

4

Т₃

Т₃

х

х

1

1

х

х

х

2

8

0

Т₃

х

х

1

Т₄

Т₄

Т₄

а) б) в)

Т₂

Т₂

Т₁

Т₁

х

1

1

х

1

х

х

х

х

1

1

Т₃

Т₃

х

х

1

х

х

1

х

1

х

1

Т₄

Т₄

г) д)

Риcунок 6.1 -а) маска; б) - діаграма Вейча-Карно для функції Т₁'; в) - діаграма Вейча-Карно для функци Т₂'; г) - діаграма Вейча-Карно для функції Тз'; д) - діаграма Вейча-Карно для функції Т₄'

клавіатура

Шифра-тор

Проце-сор і память

Буфер-ний регістр

Рисунок 6.2 - Зразок перетворення кодів даних у цифровій

електронній системі

Синтезуємо схему повного двійкового дешифратора на два входи. Така схема повинна мати чотири виходи, а її функціонування можна описати таблицею істинності (табл.6.4).

Таблиця 6.4 – Таблиця істинності для дешифратора на два входи

Входи		Функції виходів
а1	а2	D0	D1	D2	D3
0	0	1	0	0	0
0	1	0	1	0	0
1	0	0	0	1	0
1	1	0	0	0	1

Згідно з табл. 6.4. логічні вирази функцій виходів можна зобразити у вигляді ДДНФ:

; .

У загальному випадку вихідні функції D_i(a₀,a_{1, …}) дешифратора на n входів описує система логічних виразів, зображених на ДДНФ конституентами одиниці:

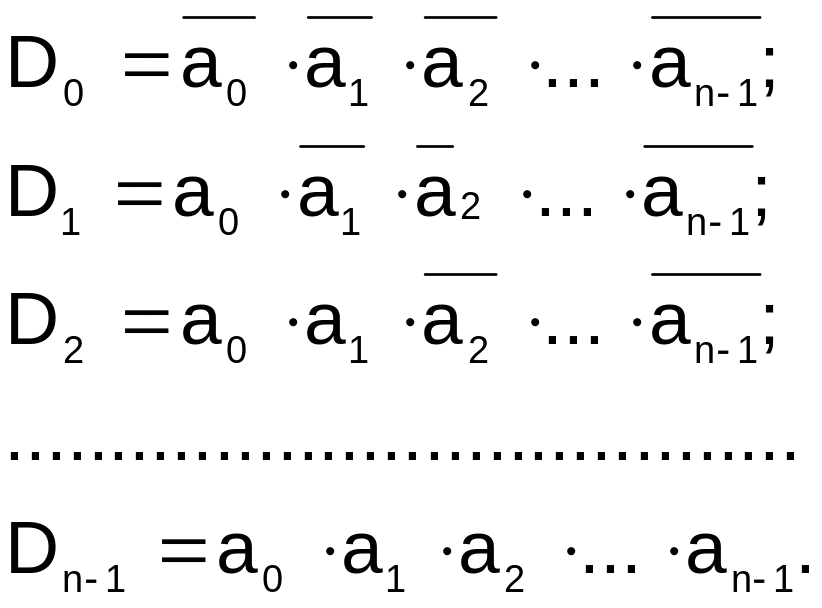
де а_і = {0,1}.

Із системи рівнянь випливає, що для побудови повного дешифратора треба мати N логічних елементів “І” з n входами в кожному (рис.6.З).

Дешифратори даного типу називають лінійними. Вони мають найбільшу швидкодію. Проте, коли вхідний код має велику розрядність, реалізувати їх важко, оскільки треба застосовувати кон'юнктори з великою кількістю входів і буде велике навантаження на джерела вхідних сигналів. Сумарну складність лінійного дешифратора визначає вираз С₁=n*2ⁿ.

Двійковим шифратром називають комбінаційну схему, яка перетворює код "1 з N" у двійковий. Шифратор виконує перетворення, зворотне дешифратору.

Коли збуджено одно з вхідних кіл шифратора, на його виходах формується двійковий код номера збудженого кола. Повний двійковий шифратор має 2ⁿ входів і n виходів. Одне з основних призначень шифратора - перетворення десяткових чиcел, введених з клавіатури, в двійковий код (тетради двійково-десяткового коду 8-4-2-1).

У цьому випадку потрібний неповний шифратор "1 з 10" в 4.

Розглянемо на його прикладі принципи синтезу схем шифратора.

Закон функціонування шифратора зобразимо таблицею істинності (табл.6.5). На підставі табл.6.5 логічні вирази у формі ДДНФ запишемо для вихідних сигналів так:

Схемно реалізувати шифратор зручно на елементах І-НЕ, тому зробимо еквівалентне перетворення одержаних співвідношень:

а₀

&

D₀

1

&

D₁

a₁

DC

1

&

D₂

a₀

0

1

1

a₁

2

2

&

3

D₃

б)

а₀ а₀ а₁ а₁

а)

Рисунок 6.З - Функціональна схема лінійного дешифратора (а) на

два входи та його умовне позначення (б)

Таблиця 6.5 – Таблиця істинності для шифратора десяткових цифр

Збуджу-вальний вхід	Виходи
	а3	а2	а1	а0
D0	0	0	0	0
D1	0	0	0	1
D2	0	0	1	0
D3	0	0	1	1
D4	0	1	0	0
D5	0	1	0	1
D6	0	1	1	0
D7	0	1	1	1
D8	1	0	0	0
D9	1	0	0	1

Схему шифратора, що реалізує дані вирази, зображено на рис.6.4.

D₉ D₈ D₇ D₆ D₅ D₄ D₃ D₂ D₁

а) б)

Рис. 6.4. Схема шифратора (а) та його умовне позначення (б)