
- •Мета і задачі дисципліни
- •1. Перелік основних тем теоретичного матеріалу
- •Практичні заняття
- •Практичне заняття №1
- •2.1. Порядок виконання роботи
- •2.2. Теоретичні відомості
- •2.2.2. Етапи структурного синтезу цифрових пристроїв
- •Синтез функцій вихо-дів та функцій збуд-ження тригерів
- •2.2.4. Перетворення логічних функцій до заданого базису елементів
- •2.3. Завдання на практичне заняття
- •Практичне заняття № 2 синтез і дослідження лічильників
- •4.1.Порядок виконання роботи
- •4.2. Теоретичні відомості
- •4.2. Котрольні запитання та завдання на
- •Практичне заняияття № 3 синтез та дослідження перетворювачів кодів
- •6.1. Порядок виконання роботи
- •6.2. Теоретичні відомості
- •6.2.1. Загальні відомості про кодування
- •6.2.3. Перетворювачі кодів для стискання і розгортання інформації
- •6.3. Завдання на практичне заняття
- •Завдання для контрольних робіт контрольна робота з дисципліни “отца”
- •Література Основна література
- •Додаткова
Складання та
налагоджування
Синтез функцій вихо-дів та функцій збуд-ження тригерів

Рисунок 2.2 - Етапи структурного синтезу цифрових автоматів
2.2.3. Мінімізація логічних функцій
При наявності набору електронних логічних елементів будь-яка логічна функція, подана у вигляді бульового виразу, може бути реалізована у вигляді електронної цифрової схеми. Наприклад, розглянемо бульовий вираз:
![]() ,
,
з якого видно, що для реалізації його у вигляді фізичної схеми необхідно три логічних елементи «І», два інвертори та один елемент «АБО» з трьома входами (рис.2.3,а).
На рис.2.3,б показана
схема, яка реалізує логічну функцію
![]() ,
що складається всього з одного електронного
логічного елемента «АБО». Аналіз роботи
нарисованих схем доводить, що вони мають
один і той самий закон функціонування,
наданий таблицею істинності на рис.2.3,в.
Наведений приклад доводить, що один і
той самий процес перетворення цифрових
сигналів може виконуватись схемами
різної скпадності, а значить, і вартості.
Отже, при проектуванні цифрових пристроїв
потрібно звертати увагу на невиправдане
подорожчання схем.
,
що складається всього з одного електронного
логічного елемента «АБО». Аналіз роботи
нарисованих схем доводить, що вони мають
один і той самий закон функціонування,
наданий таблицею істинності на рис.2.3,в.
Наведений приклад доводить, що один і
той самий процес перетворення цифрових
сигналів може виконуватись схемами
різної скпадності, а значить, і вартості.
Отже, при проектуванні цифрових пристроїв
потрібно звертати увагу на невиправдане
подорожчання схем.
За критерій вартості логічної схеми беруть її складність, яка визначається сумарною кількістю входів логічних елементів. Наприклад, складність Су1, схеми на рис.2.3,а – Су1 = 11, а складність схеми на рис.2.3,б –Су2 = 2.
Оскiльки існує однозначна відповідність між бульовою функцією та логічною схемою, яка її реалізує, то зменшення складності схеми можна досягти шляхом мінімізації бульової функції - знаходження найбільш простого виразу для заданої функції, еквівалентного початковому.
Найчастіше мінімізацію проводять для логічної функції, яка подана в досконалій диз'юнктивній нормальній формі (ДДНФ), отримуючи при цьому мінімальну ДНФ.
Найбільш поширеними методами мінімізації логічних функцій є метод мінімізації за допомогою діаграм Вейча-Карно та метод Квайна- МакКласкі. Діаграми Вейча-Карно зручно застосовувати для мінімізації бульових функцій, які містять не більше 4-6 змінних. Дані діаграми являють собою спеціально організовані таблиці істинності. Кількість клітинок в таблиці повинна відповідати кількості можливих наборів аргументів.
Якщо кількість
змінних n,
на яких задана бульова функція, парна,
то кількість рядків та стовпчикiв в
таблиці дорівнює 2n/2,
якщо непарна, то беруть таку кількість
рядків, яка дорівнює
![]() ,
а кiлькiсть стовпчиків –
,
а кiлькiсть стовпчиків –
![]() .
На рис.2.4 показані діаграми Вейча-Карно
для функцій двох, трьох, чотирьох та
п'яти аргументів. Набори в клітинках
таблиці розміщені так, що два сусідні
набори в стовпчику або рядку відрізняються
значенням однієї змінної - в одному
наборі вона з запереченням, а в другому
– без заперечення. При такому розміщенні
будь-якi два сусідні набори можуть
склеюватися. Відповідна розмітка рядків
та стовпчикiв діаграм Вейча-Карно
символами змінних показана на рис.2.4.
.
На рис.2.4 показані діаграми Вейча-Карно
для функцій двох, трьох, чотирьох та
п'яти аргументів. Набори в клітинках
таблиці розміщені так, що два сусідні
набори в стовпчику або рядку відрізняються
значенням однієї змінної - в одному
наборі вона з запереченням, а в другому
– без заперечення. При такому розміщенні
будь-якi два сусідні набори можуть
склеюватися. Відповідна розмітка рядків
та стовпчикiв діаграм Вейча-Карно
символами змінних показана на рис.2.4.
Х1
І
І
Х1





Х2
Х2



Х1
Х1
І
Y2
Х2
Y1

АБО
АБО


Х2
Х1
І
б)
Х2

а)
-
Входи
Виходи
Х2
Х1
Y1
Y2
0
0
0
0
0
1
1
1
1
0
1
1
1
1
1
1
в)
![]() , Y2
= X1
+ X2
, Y2
= X1
+ X2
Рисунок 2.3 - а) – структурна схема електронного пристрою, яка реалізує функцію ; б) – схема, яка реалізує функцію Y2 = X1+X2; в) – таблиця, яка задає закон функціонування обох схем
Кожна змінна
розбиває діаграму на дві половини -
п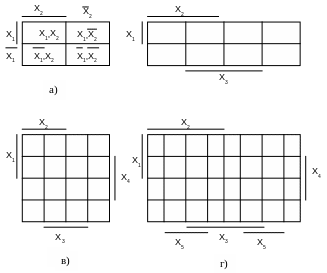 оловину
Х та половину
оловину
Х та половину
![]() .
.
Рисунок 2.4 - Діаграми Вейча-Карно для двох, трьох,
чотирьох та п'яти логічних змінних
Частина діаграми, яка відповідає неінверсним аргументам, на рис. 2.4. відмічена жирною лінією.
Якщо бульова функція надана таблицею істинності, то «1» заповнюються клітинки діаграми Вейча, які відповідають наборам значень змінних, на яких функція перетворюється в одиницю (рис.2.5). Клітинки, які відповідають нульовим значенням, залишаються пустими. Потім за одержаними діаграмами проводять мінімізацію логічної функції. Для цього спочатку виконують побудову контурів, якi охоплюють клітинки з одиницями, дотримуючись наступних правил:
1) контур повинен бути прямокутним або квадратним та містити тільки клітинки з одиницями;
2) кількість клітинок всередині контуру повинна бути цілим степенем двійки – 1,2,4,8, ...;
3) всі одиниці повинні бути охоплені контурами;
4) кожний контур повинен охопити максимально можливу кiлькiсть одиниць;
5) при проведенні контурів нижній і верхній рядки та лівий і правий стовпці вважаються сусідніми.
Таблиця істинності Діаграма Вейча-Карно
Х2
Х2 Входи
|
Виходи
|
|
Х1
1
|
Х1 |
F(X)
|
|
0 |
1
|
Х1
1
1
|
1 |
1
|
1
|
0 |
1
|
1
|
1 |
0
|
Рисунок 2.5 - Порядок заповнення діаграм Вейча-Карно за таблицею
істинності логічної функції
Загальна кількість імплікант в мінімальній ДНФ буде дорівнювати числу контурів. Чим більше одиниць в контурі, тим коротша імпліканта, яка описує його.
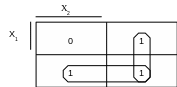
Приклад 1. Мінімізувати логічну функцію двох змінних, яка задана таблицею істинності на рис.2.5.
Рішення: Відповідно до вищенаведених правил будуємо контури на діаграмі Вейча-Карно (табл.2.1).
 Таблиця
2.1 –
Проведення контурів на діаграмі
Вейча-Карно
Таблиця
2.1 –
Проведення контурів на діаграмі
Вейча-Карно
Щоб знайти просту імпліканту, яка описує контур, необхідно з'ясувати, від яких змінних не залежить даний контур. Оскільки вертикальний контур в табл. 2.1 охоплює рядки з х1 та х1 , то х1 в імпліканту, яка описує даний контур, не входить (по ній два сусідні набори склеюються). Міркуючи аналогічно, з'ясовуємо, що в просту імпліканту, яка описує горизонтальний контур, змінна х2 входити не буде. Отже, мінімальна ДНФ логічної функції, що задана таблицею істинності на рис.2.5, має вигляд:
![]() .
.
Приклад 2. Мінімізувати логічну функцію трьох змінних, задану бульовим виразом:
![]() .
.
Рішення: Спочатку приведемо його до ДНФ:
Відповідно до ДНФ (2.1) логічної функції заповнимо діаграму
Вейча-Карно для трьох змінних (рис.2.6).
Р исунок
2.6
- Побудова
діаграми Вейча-Карно для ДНФ логічної
исунок
2.6
- Побудова
діаграми Вейча-Карно для ДНФ логічної
функції трьох змінних
На діаграмі проводимо один контур з одиницями так, як це показано на рис.2.6. Мінімальна ДНФ заданої функції має вигляд:
![]() .
.





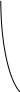 0
0 0
0
