4.3. Сущность и значение средних показателей

В процессе обработки и обобщения статистических данных возникает необходимость определения средних величин. Как правило, индивидуальные значения одного и того же признака у различных единиц совокупности неодинаковы, но при этом невозможно исследовать каждую единицу. В данном случае прибегают к расчету средних величин, так как они отражают типичные черты и дают обобщенную характеристику однотипных явлений по одному из варьирующих признаков. Средняя величина отражает объективный уровень, достигнутый в процессе развития явления к определенному моменту или периоду.

Средняя величина – это обобщающая характеристика изучаемого признака в исследуемой совокупности, отражающая его типичный уровень в расчёте на единицу совокупности в конкретных условиях места и времени.

Широкое применение средних объясняется тем, что они обладают рядом положительных свойств, делающих их незаменимыми при анализе явлений общественной жизни. Одно из свойств средних, заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значение признака у отдельных единиц совокупности могут колебаться в ту или иную сторону под влиянием множества факторов как случайных, так и основных. Сущность средней в том и заключается, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения вызванные действием факторов основных.

В статистике выработан ряд правил, которые следует учитывать при расчете средних величин:

• при определении средней величины в каждом конкретном случае нужно исходить из качественного содержания осредняемого признака, учитывать взаимосвязь изучаемых признаков, а также имеющиеся для расчёта данные;

• средняя величина должна рассчитываться по однородной совокупности;

• общие средние должны подкрепляться групповыми средними (групповые средние, т.е. расчёт средней в группах сформированных по признакам различия, более полно отражает закономерности, а общая средняя показывает лишь общий результат);

• средняя величина характеризует изучаемую совокупность по одному признаку, следовательно, для более детальной характеристики совокупности по ряду существенных признаков необходимо располагать системой средних величин, которые могут описать явление с разных сторон.

Средние величины делятся на два класса:

• степенные средние; к ним относят такие наиболее известные и часто применяемые виды, как арифметическая средняя, гармоническая, геометрическая квадратическая;

• структурные (описательные) средние, в качестве которых рассматриваются мода, медиана, квартиль, дециль, перцентиль.

Выбор вида средней зависит от цели исследования, экономической сущности осредняемого показателя и характера имеющихся исходных данных.

4.4 Степенные и структурные средние

Рассмотрим некоторые виды степенных и структурных средних, которые наиболее часто используются в статистике.

Степенные средние в зависимости от представления исходных данных исчисляются в двух формах: простой и взвешенной. Простая средняя считается по несгруппированным данным и имеет следующий общий вид:

(4.1)

где - значение средней величины;

х_i - индивидуальное значение признака;

k – показатель степени средней величины;

n – объем изучаемой совокупности.

Взвешенная средняя считается по сгруппированным данным, представленных в виде дискретных или интервальных рядов распределения:

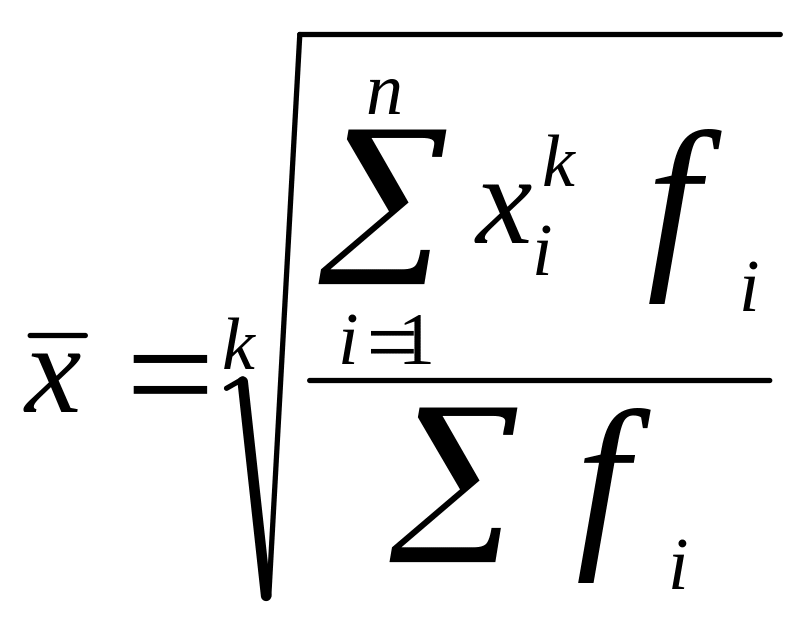
(4.2)

где f_i – частота, показывающая, сколько раз встречается признак в совокупности

Придавая различные значения k получают следующие виды степенных средних:

• средняя гармоническая, если k = - 1;

• средняя геометрическая, если k = 0;

• средняя арифметическая, если k = 1;

• средняя квадратическая, если k = 2;

• средняя кубическая, если k = 3 и т.д.

Рассмотрим некоторые виды средних, которые наиболее часто используются в статистике.

Средняя арифметическая простая (невзвешенная) равна сумме отдельных значений признака, деленной на число этих значений.

(4.3)

Пример

Имеются следующие данные о производстве рабочими продукции А за смену:

№ рабочего	1	2	3	4	5	6	7	8	9	10
Выпущено изделий за смену, шт	16	17	18	17	16	17	18	10	11	18

В данном примере варьирующий признак - выпуск продукции за смену.

Численные значения признака (16, 17 и т. д.) называют вариантами. Определим среднюю выработку продукции рабочими данной группы:

шт.

Простая средняя арифметическая применяется в случаях, когда имеются отдельные значения признака, т.е. данные несгруппированы. Если данные представлены в виде рядов распределения или группировок, то средняя исчисляется иначе.

Пример

Имеются следующие данные:

Группы рабочих по количеству произведенной продукции за смену, шт.	Число рабочих, f i	Середина интервала, хi	xi fi
3 — 5	10	4	40
5 — 7	30	6	180
7 — 9	40	8	320
9 — 11	15	10	150
11 — 13	5	12	60
ИТОГО	100		750

Исчислим среднюю выработку продукции одним рабочим за смену. Исходные данные представлены в виде ряда распределения, следовательно, воспользуемся формулой арифметической взвешенной:

(4.4)

Из формулы 4.4 видно, что средняя зависит не только от значений признака, но и от их частот, т.е. от состава совокупности, от ее структуры. Статистический материал в результате обработки может быть представлен не только в виде дискретных рядов распределения, но и в виде интервальных вариационных рядов с закрытыми или открытыми интервалами. Рассмотрим расчет средней арифметической для таких рядов.

В данном ряду варианты осредняемого признака (продукция за смену) представлены не одним числом, а в виде интервала "от - до". Рабочие первой группы производят продукцию от 3 до 5 шт., рабочие второй группы - от до 7 шт. и т. д. Таким образом, каждая группа ряда распределения имеет нижнее и верхнее значения вариант, или закрытые интервалы.

Чтобы применить 4.4, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения интервала. Так, для первой группы дискретная величина х будет равна:

(3 + 5) / 2 = 4

Дальнейший расчет производится обычным методом определения средней арифметической взвешенной:

Итак, все рабочие произвели 750 шт. изделий за смену, а каждый в среднем произвел 7,5 шт.

В интервальных рядах распределения с открытыми интервалами условно величина интервала первой группы принимается равной величине интервала последующей, а величина интервала последней группы - величине интервала предыдущей. Дальнейший расчет аналогичен изложенному выше.

В практике экономической статистики иногда приходится исчислять среднюю по групповым средним или по средним отдельных частей совокупности (частным средним). В таких случаях за варианты (х) принимаются групповые или частные средние, на основании которых исчисляется общая средняя как обычная средняя арифметическая взвешенная.

Основные свойства средней арифметической.

Средняя арифметическая обладает рядом свойств:

1. От уменьшения или увеличения частот каждого значения признака х в n раз величина средней арифметической не изменится.

Если все частоты разделить или умножить на какое-либо число, то величина средней не изменится.

2. Общий множитель индивидуальных значений признака может быть вынесен за знак средней:

3. Средняя суммы (разности) двух или нескольких величин равна сумме (разности) их средних:

4. Если х = с, где с - постоянная величина, то .

5. Сумма отклонений значений признака х от средней арифметической равна нулю:

Наряду со средней арифметической, в статистике применяется средняя гармоническая величина, обратная средней арифметической из обратных значений признака. Как и средняя арифметическая, она, может быть, простой и взвешенной.

Пример

Бригада токарей была занята обточкой одинаковых деталей в течение 8-часового рабочего дня. Первый токарь затратил на одну деталь 12 мин, второй - 15 мин., третий - 11, четвертый - 16 и пятый - 14 мин. Определите среднее время, необходимое на изготовление одной детали.

Если учитывать, что каждый токарь за смену сделал одну деталь, то решение выглядит следующим образом:

Но в течение дня отдельными рабочими было изготовлено различное число деталей. Для определения числа деталей, изготовленных каждым рабочим, воспользуемся следующим соотношением:

Среднее время выполнения одной детали = все время затраченное на работу / количество выполненных деталей

Число деталей, изготовленных каждым рабочим, определяется отношением всего времени работы к среднему времени, затраченному на одну деталь. Тогда среднее время, необходимое для изготовления одной детали, равно:

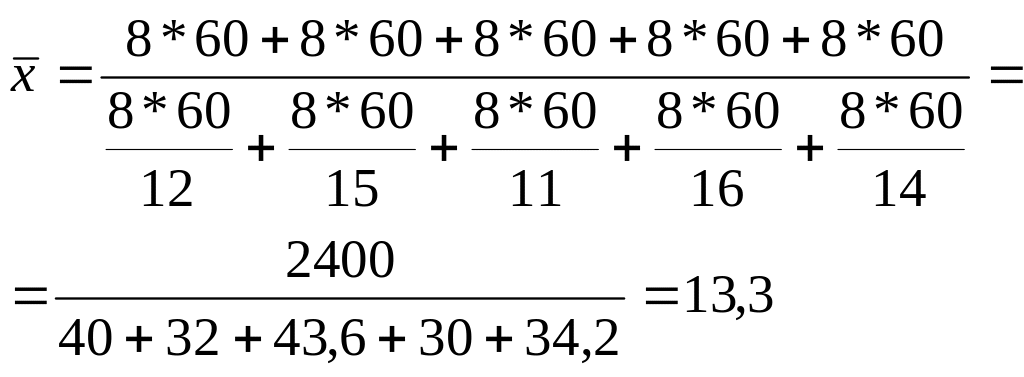
Это же решение можно представить иначе:

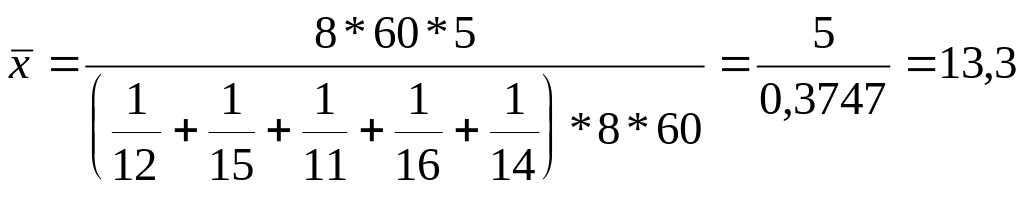
Таким образом, формула для расчета средней гармонической простой будет иметь вид:

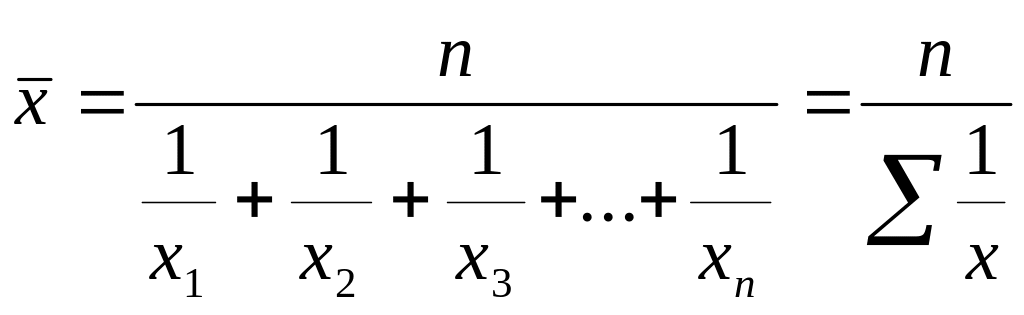
(4.5)

где n – объем исследуемой совокупности.

Пример: Издержки производства и себестоимость единицы продукции А по трем заводам характеризуются следующими данными:

№ завода	Издержки производства, тыс.руб.	Себестоимость единицы продукции, руб.
1	200	20
2	460	23
3	110	22

Исчислим среднюю себестоимость изделия по трем заводам. Главным условием выбора формы средней является экономическое содержание показателя и исходные данные.

Средняя себестоимость изделия = Суммарные издержки производства / количество изделий

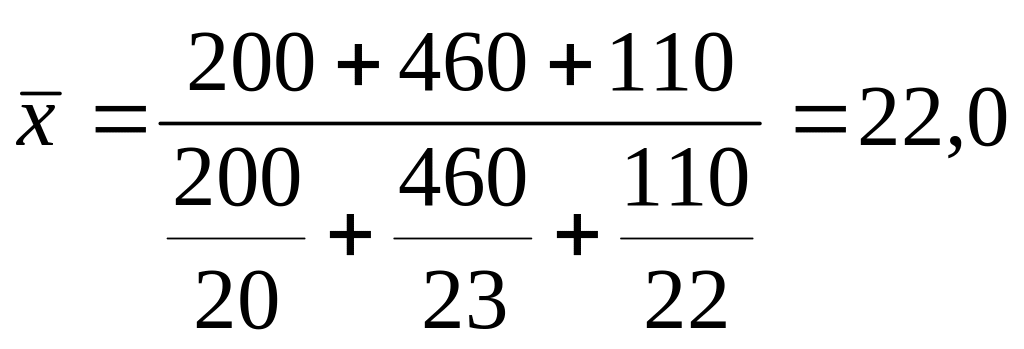руб.

Таким образом, формулу для расчета средней гармонической взвешенной можно представить в общем виде:

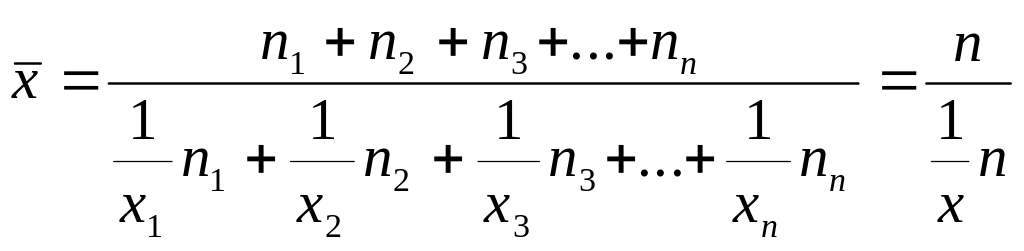
(4.6)

Геометрическая средняя наиболее часто используется в анализе динамики для определения среднего темпа роста. Ее расчет может производиться по формулам 4.7, 4.8.

• простая (невзвешенная):

(4.7)

• взвешенная:

(4.8)

Средняя квадратическая наиболее часто используется при расчете показателей вариации (подробнее см. гл 5), а также для вычислений большинства сводных расчетных показателей.

• невзвешенная (простая):

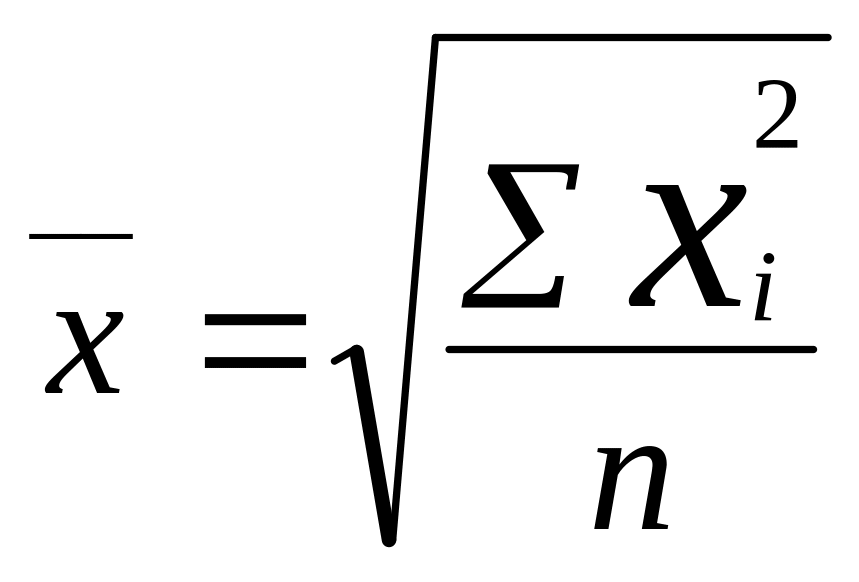
(4.9)

• взвешенная:

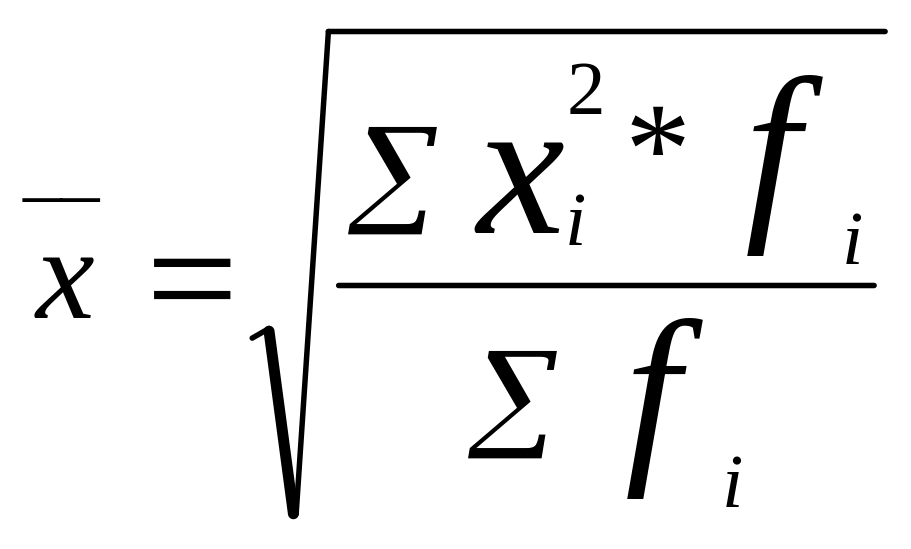
(4.10)

В статистике используются средние величины и более высоких порядков, например, средняя кубическая и др.

Величины степенных средних, рассчитанных на основе одних и тех же индивидуальных значений признака при различных значениях степени k, не одинаковы. Чем выше показатель степени k, тем больше значение средней величины (если индивидуальные значения признака варьируют). Отсюда имеем следующее соотношение, называемое правилом мажорантности средних:

Структурные средние применяются для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным её расчёт не может быть выполнен.

Медиана – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.

Если данные о значениях признака х представлены в интервальном вариационном ряду с равными интервалами, то медиана определяется по формуле 4.11.

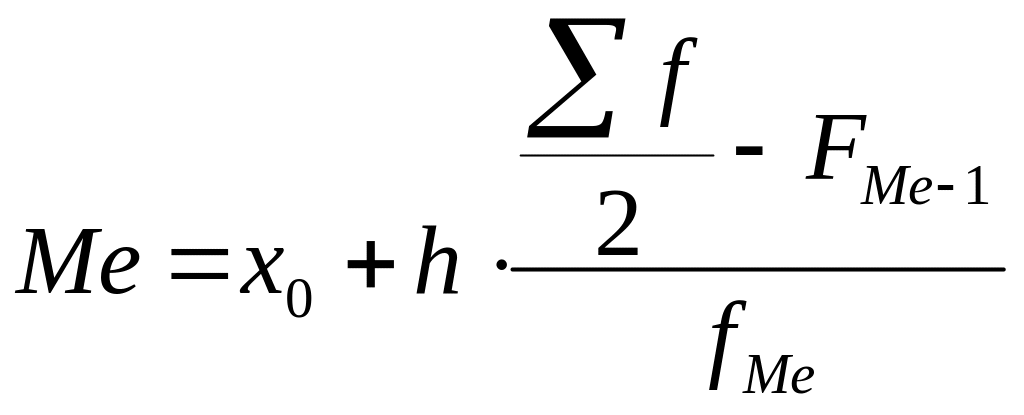
(4.11)

где - нижняя граница интервала, который содержит медиану;

- величина медианного интервала;

- сумма частот или общее число наблюдений;

- накопленная частота в интервале, предшествующем медианному;

- число наблюдений или частота медианного интервала.

Мода – значение признака, наиболее часто встречающееся в исследуемой совокупности.

В дискретном ряду распределения значения моды определяются визуально. Для интервального ряда с равными интервалами величина моды определяется по формуле:

(4.12)

где: - нижняя граница модального интервала;

h - величина модального интервала;

f_m- частота модального интервала;

f_m-1 - частота интервала, предшествующего модальному;

f_m+1 - частота интервала, следующего за модальным.

Наряду с нахождением медианы в вариационных рядах распределения можно отыскать значение признака у единиц, делящих ряд на 4 равные части (“квартили”), на 10 равных частей (“децили”) или 100 равных частей (“перцентили”).

Использование в анализе вариационных рядов распределения рассмотренных выше характеристик позволяет более глубоко и детально охарактеризовать изучаемую совокупность.