2.4. Пассивные связи и лишние степени свободы

В некоторых механизмах имеются звенья, наличие которых не влияет на подвижность механизма, они налагают пассивные или избыточные условия связи. Такие звенья называются пассивными. Примером механизма с пассивными условиями связи является механизм параллельных кривошипов (рис. 2.4). Степень подвижности этого механизма , но фактически она будет составлять . В данном случае звено 4 (EF) налагает избыточные пассивные условия связи и их можно исключить, при этом степень подвижности механизма не изменится.

а б

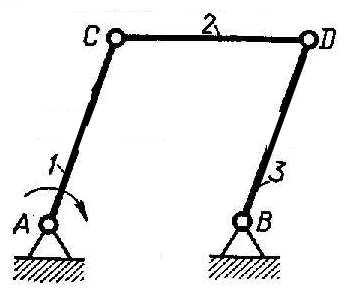
Рис. 2.4. Механизм с пассивными условиями связи:

1. Механизм с пассивной связью ef – ;

2. Механизм без пассивной связи – .

В механизмах пассивные звенья вводят для увеличения жесткости, лучшего распределения нагрузки и т.д.

В кулачковом механизме, изображенном на рис. 2.5, степень подвижности равна , где количество подвижных звеньев n =3, количество кинематических пар 5 класса p₅ =3 – А (1, 0), B (2, 0) C(2, 3); количество кинематических пар 4 класса p₄ =1 – D (1, 3). Здесь вторую подвижность вносит ролик 3. Если ролик затормозить, то характер движения коромысла 2 не измениться. Следовательно, степень свободы, вносимая роликом 3 является “лишней”. При заторможенном ролике степень подвижности равна , где количество подвижных звеньев n =2, количество кинематических пар 5 класса p₅ =2 – А (1, 0), B (2, 0); количество кинематических пар 4 класса p₄ =1 – D (1, 3).

Звенья, создающие лишние степени свободы, используют в механизме для улучшения условий работы, повышения КПД (замена трения скольжения трением качения) и т.д. При структурном анализе пассивные звенья и лишние степени свободы условно исключают.

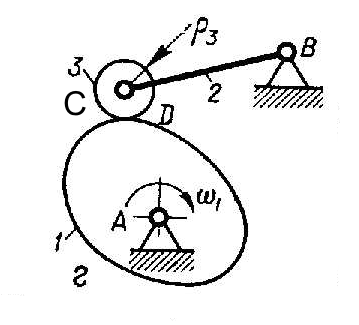
Рис. 2.5. Кинематическая схема кулачкового механизма

2.5. Классификация механизмов

В основу современной классификации механизмов положена классификация, разработанная И.И. Артоболевским. В соответствие с этой классификацией механизмы объединяются в классы от первого и выше по структурным признакам. Механизм первого класса – исходный механизм, состоит из ведущего звена и стойки (рис. 2.6), которые соединены кинематической парой пятого класса. Механизмы второго, третьего т.е. более высоких классов, образуются последовательным соединением к исходному механизму кинематических цепей, у которых степень подвижности равна нулю.

Рис. 2.6. Исходный механизм (механизм 1 класса)

2.6. Структурные группы

Структурной группой называется кинематическая цепь, которая, будучи присоединенной свободными элементами пар к неподвижной стойке, обладает нулевой степенью подвижности, . Положим, что в состав структурной группы входят кинематические пары только 5 класса, тогда формула Чебышева будет записана в виде , откуда

,

из этой формулы следует, что структурная группа может состоят из двух звеньев (n=2) и трех кинематических пар (p₅=3); четырех звеньев (n=4) и шести кинематических пар (p₅=6) и т.д.

Структурные группы делятся на классы в зависимости от класса контура. Контуром называют замкнутую область части плоскости, занятой звеном или ограниченной со всех сторон звеньями. Класс контура определяется числом внутренних кинематических пар, входящих в этот контур. Рассмотрим контур структурной группы, показанной на рис. 2.7. а). Этот контур второго класса, поскольку плоскость, занятая звеном (например, АВ рис.2.7 б) и в)) имеет две внутренних кинематических пары – А и В. Структурная группа, показанная на рис. 2.7 г), имеет наибольший контур FВС с тремя кинематическими парами, поэтому этот контур третьего класса. На рис. 2.7 д) структурная группа имеет три контура: АВС – контур третьего класса, FDE – контур третьего класса, CBDF – контур четвертого класса, поэтому это группа 4 класса.

Рис. 2.7. Контуры различных классов

Наиболее распространенными являются группы второго класса. В состав группы второго класса входят два звена и три пары пятого класса (рис. 2.8).

Вид структурной группы второго класса назначается от числа и взаимного расположения вращательных и поступательных пар в ней. Структурная группа 2^ого класса, 1^ого вида имеет три вращательные пары (В-В-В), 2^ого вида имеет две вращательные пары и одну крайнюю пару поступательную (В-В-П), 3^ого вида имеет две вращательные пары и одну среднюю пару поступательную (В-П-В).

Класс механизма определяется по высшему классу группы, которая входит в его состав. Для определения класса механизма необходимо выделить из него структурные группы, начиная от наиболее удаленных от ведущего звена.

Рис. 2.8. Наиболее распространенные структурные группы 2 класса