6. Числові рівності, властивості істинних числових рівностей
Означення. Числова рівність – це два числові вирази між якими стоїть знак дорівнює.
a = b – загальний вигляд числової рівності.
5 + 1 = 8 – 2 – істинна числова рівність.
Означення. Числова рівність істинна, якщо значення числових виразів, що стоять у лівій і правій частинах рівності, співпадають.
Властивості істинних числових рівностей:
Відношення «дорівнює» на множині R володіє властивостями:
рефлективності:
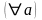
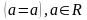
симетричності:
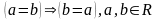
транзитивності:
.монотонність додавання:
.
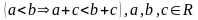(Якщо до обох частин істинної числової рівності а = в додати один і той самий числовий вираз с, що має смисл, то отримаємо також істинну числову рівність а + с = b + с, а = b => а + с = b + с).
Отже, це відношення є відношенням еквівалентності.
5)
монотонність множення :
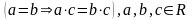
(Якщо обидві частини істинної числової рівності а = в помножити на один і той самий числовий вираз с, що має смисл, то отримаємо також істину числову рівність ас = bс, а = b => ас = bс).
Питання для узагальнення
Що називається числовою рівністю?
Назвіть властивості істинних числових рівностей?
7. Числові нерівності, властивості істинних числових нерівностей
Нехай а і b – два числові вирази. З’єднаємо їх знаком > або <. Отримаємо речення а > b (а < b), яке називають числовою нерівністю.
Н.: 6 + 2 > 13 – 7 – істинна числова нерівність.
Означення. Два числові вирази а і b, сполучені знаками «>» (більше) або «<» (менше) називають числовою нерівністю:
a > b або a < b – числові нерівності.
Наприклад. 45 > 23 + 12; 5 · 7 < 5 · 8; 200 < 300 – 100.
Нерівності – це також висловлення, які можуть бути істинними або хибними.
Властивості істинних числових нерівностей:
Відношення «менше» на множині R володіє властивостями:
антисиметричності:
,
транзитивності:
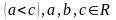;монотонність додавання: ;
(Якщо до обох частин істинної числової нерівності а > b додати один і той самий числовий вираз с, що має смисл, то отримаємо також істинну числову нерівність а + с > в + с).
4)
монотонність множення:
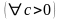
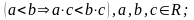
(Якщо обидві частини істинної числової нерівності а > в помножити на один і той самий числовий вираз с, що має смисл і набуває додатне значення, то отримаємо істинну числову нерівність ас > bс).
5)
монотонність множення:
(Якщо обидві частини істинної числової нерівності а > b помножити на один і той самий числовий вираз с, що має смисл і набуває від’ємне значення, то, щоб отримати істинну числову нерівність, необхідно знак нерівності поміняти на протилежний ас < bс).
Питання для узагальнення
Що називається числовою нерівністю?
Назвіть властивості істинних числових нерівностей?
Заключна частина
Загальний висновок
Числовий вираз – це запис, що складається з чисел, з’єднаних знаками арифметичних дій. Н.: 3 + 7, 24 : 8, (25 + 3) · 2 – 17.
Вираз зі змінною – це вираз, що містить у собі змінну, позначену латинською літерою.
Н.: 2а + 3, 3х – 5.
Числа, які можна підставляти замість змінної частини у вираз, називають значеннями змінної.
Область визначення виразу – це множина дійсних значень змінної, при якій вираз має зміст, тобто можна виконати усі арифметичні дії.
Н.: 3 – 4у – область визначення R.
;
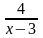х – 3 ≠ 0,
х ≠ 3, D
.
У математиці розглядають вирази, які містять одну зміну, дві. три і т. д.
Вираз 3х + 4у містить дві змінні, 5х – (2у – 7z) – вираз із трьома змінними.
Числова рівність – це два числові вирази між якими стоїть знак дорівнює. a = b – загальний вигляд числової рівності
Числова рівність істинна, якщо значення числових виразів, що стоять у лівій і правій частинах рівності, співпадають.
Два числові вирази а і b, сполучені знаками «>» (більше) або «<» (менше) називають числовою нерівністю.
Запитання для узагальнення студентам
Що є алфавітом математичної мови?
Що називається числовим виразом?
Що називається значенням числового виразу?
Який вираз називається виразом зі змінною?
Що називається областю визначення виразу зі змінною?
Які вирази називаються тотожно рівними?
Що називається числовою рівністю?
Що називається числовою нерівністю?
Сформулюйте властивості істинних числових рівностей і нерівностей?
Повідомлення домашнього завдання