Текст лекції з математики для студентів і курсу педагогічного факультету рдгу

Тема: Подільність цілих невід’ємних чисел. НСД та НСК чисел.

План: 1. Поняття відношення подільності і його властивості.

2. Подільність суми, різниці добутку.

3. Ознака подільності Б. Паскаля.

4. Ознаки подільності на 2, 3, 4, 5, 9, 25 у десятковій системі числення.

5. Прості і складені числа. Нескінченність множини простих чисел. Решето Ератосфена.

6. Основна теорема арифметики натуральних чисел.

7. Дільники та кратні: СД і СК; НСД і НСК.

8. Обчислення НСД та НСК чисел способом канонічного розкладу на прості множники та за алгоритмом Евкліда.

9. Ознаки подільності на складені числа.

Зміст лекції:

1. Поняття відношення подільності та його властивості.

На множині N₀ а може дорівнювати нулю, але

Відношення будемо розглядати на множині N.

Відношення подільності є відношенням нестрогого порядку, оскільки володіє такими властивостями:

а) рефлективність:

Приклад:

б) антисиметричність:

в) транзитивність:

Доведення:

Доведено.

2. Подільність суми, різниці, добутку.

а)

Доведення:

=cr

Доведено.

Приклад: a=12, b=18, c=6; a+b=12+18=30;

Обернене твердження хибне.

Приклад:

б)

Доведення:

Доведено.

Приклад:

Обернене твердження хибне.

Приклад:

в) якщо хоч один із множників a та b перебуває у відношенні подільності з числом с, то й добуток перебуває у відношенні подільності з числом с.

1)

=cr

2)

Доведено.

105

3. Ознака подільності Паскаля.

Ознака подільності – це твердження, яке дозволяє за записом числа в десятковій системі числення встановити, чи ділиться дане число на деяке інше число, не виконуючи дію ділення.

Ознака подільності Паскаля:

Якщо один доданок не ділиться на число m, а всі інші діляться на число m, то їх сума не ділиться на число m.

Доведення:

Позначимо через а через

Тоді Отже, треба довести, що Доведемо ознаку методом від супротивного. Припустимо, що , тоді з рівності

– за припущенням, – за подільністю суми. Отже, за подільністю різниці.

А це суперечить умові, бо за умовою . Отже, припущення про те, що є хибним, а тому . Ознака доведена.

Ознаку Паскаля використовують для доведення всіх інших ознак незалежно від системи числення. Ми розглянемо ознаки в десятковій системі числення.

4. Ознаки подільності на 2 і 5; 4 і 25; 3 і 9.

а) ознака подільності на 2 і 5.

Приклад:

1)

2)

Для того, щоб число ділилося на 2, необхідно і достатньо, щоб остання цифра його десяткового запису була парною (тобто 0, 2, 4, 6, 8).

Доведення:

Позначимо число, записане всіма цифрами, крім останньої, через а , тобто Тоді Отже доведемо:

Необхідність:

Звідси

- за умовою.

Отже, тобто за подільністю різниці. Необхідність доведена.

Достатність:

– за подільністю добутку.

- за умовою.

- за подільністю суми, а отже . Доведено достатність.

Теорема (ознака подільності на 2) доведена.

Цілком аналогічно доводиться ознака подільності на 5, лише замість цифри (останньої в записі числа) слід розуміти цифри 0 або 5.

(Доведення записати самостійно)

б) ознака подільності на 4 і 25.

Приклад:

Для того, щоб число s ділилось на 4, необхідно і достатньо, щоб число , утворене двома останніми цифрами його запису ділилося на 4.

Доведемо необхідність:

b=s - 100; s 4 – за умовою, ( 100) 4 за подільністю добутку, а тому

(s - ) за подільністю різниці, а це означає, що b .

Отже , необхідність доведена.

Доведемо достатність: (b )(s )

S= +b.

- за подільністю добутку, бо .

- за умовою. Отже, - за подільністю суми. А отже, . Достатність доведена.

Ознака подільності на 4 доведена.

Аналогічно доводиться ознака подільності на 25, тобто в наведеному записі, замінивши число 4 на 25 дістанемо запис доведення ознаки подільності на 25:

Записати доведення самостійно, маючи на увазі, що число (b), утворене двома останніми цифрами може бути таким: .

в) ознака подільності на 3 і 9.

Приклади:

234 = 2  100 + 3  10 + 1 = 2 10² + 3 10¹ + 1 10⁰ =

Доведемо в загальному вигляді: Для того, щоб число ділилося на 3, необхідно й достатньо, щоб сума цифр його запису ділилася на 3.

,

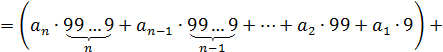
Позначимо:

Отже,

Як очевидно, завжди тому треба довести:

Для того, щоб число s ділилося на 3, необхідно і достатньо, щоб сума цифр, яким записане це число, ділилося на 3.

Необхідність

- за умовою,

- за подільністю суми та добутку.

(s – s₁) 3 – за подільністю різниці. Отже, s₂ 3.

Необхідність доведена.

Достатність s₂ 3 s 3;

S₁ +S₂=S, S₁ 3 – за подільністю суми і добутку;

S₂ 3 – за умовою.

Отже, - за подільністю суми. А тому, . Достатність доведена. Теорема доведена. Аналогічно доводиться ознака подільності на 9. Записати доведення самостійно.