Расчет и построение отклика аналогового фильтра на сигнал
Расчет прохождения периодического сигнала через ЛЭЦ
Периодический сигнал, проходя через ЛЭЦ, не теряет своей периодической природы, поэтому сигналы на входе и выходе линейной цепи можно представить бесконечной суммой непериодических сигналов, сдвинутых друг относительно друга на период.
Постоянная составляющая на выходе прямо пропорциональна значению
коэффициента
передачи при
.
Амплитуды гармонических колебаний
умножаются на значения модуля комплексной передаточной функции на
частотах . Начальные фазы гармонических колебаний суммируются
со значениями фазочастотной характеристики ЛЭЦ на частотах
(3.1)
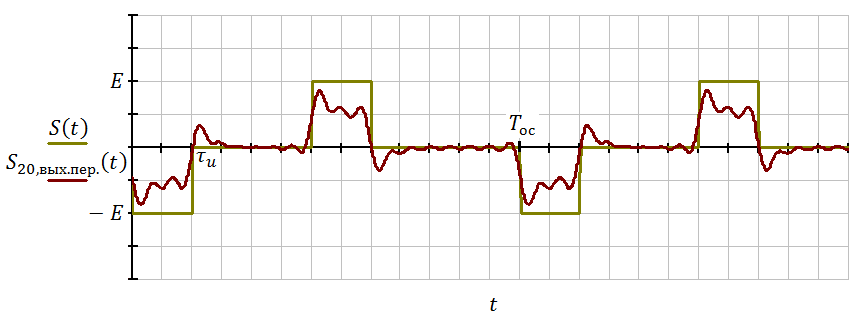
Рисунок 3.1 – Периодический сигнал на входе и выходе ЛЭЦ
В приложении Б показаны периодические сигналы на выходе ЛЭЦ из разного количества гармонических колебаний. При малом числе гармоник временное представление на выходе имеет пульсирующий характер. Это связано из-за ограниченной ширины спектра сигнала.
Расчет прохождения непериодического сигнала через ЛЭЦ
(3.2)
где – переходная характеристика
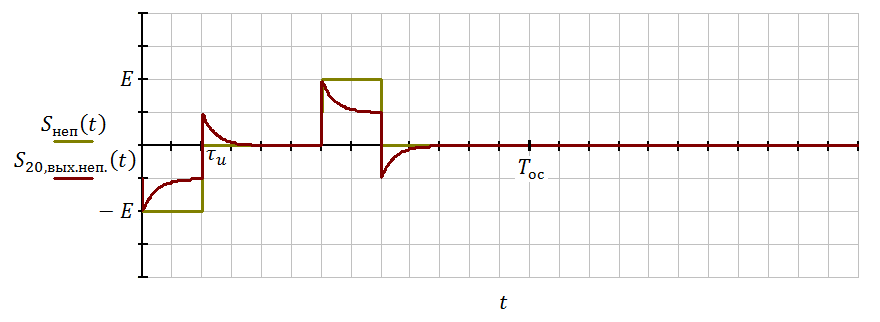
Рисунок 3.2 – Непериодический сигнал на входе и выходе ЛЭЦ
Выводы
В данной курсовой работе был рассмотрен сигнал, представляющий собой последовательность импульсов прямоугольной формы.
При нахождении спектральной плотности заданного сигнала выяснилось, что если анализируемый сигнал периодический, то его спектр дискретный, если непериодический, то его спектр сплошной. Спектральная плотность – непрерывная функция частоты. Комплексный коэффициент – дискретная функция частоты. Так как заданный сигнал представляет собой нечетную функцию времени, то спектральная плотность является чисто мнимой функцией частоты.
Форма синусоидального напряжения (или тока) на выходе любой линейной электрической цепи остается синусоидальной, а амплитуда напряжений и его начальная фаза изменяются. Поэтому при рассмотрении воздействия на электрические цепи несинусоидальных напряжении (токов) во многих случаях целесообразно представить их в виде некоторой суммы синусоидальных колебаний. В основе расчета ЛЭЦ, находящихся под воздействием периодических негармонических сигналов, лежит принцип суперпозиции (или наложения). Согласно этому принципу, разложенный в ряд Фурье сигнал воздействует на ЛЭЦ по частям и поочередно. Расчет отклика цепи на воздействие постоянной составляющей сводится к расчету резистивной цепи, поскольку имеющиеся в ней емкости заменяем на разрыв, а индуктивности на короткое замыкание. Расчет отклика цепи на каждую из гармоник осуществляем с помощью комплексного коэффициента передачи цепи. Суммируя все полученные отклики, получаем отклик ЛЭЦ на заданное негармоническое периодическое воздействие. Из выполненной работы заметим, что ФВЧ заостряет входной сигнал.
Как видим, ширина спектра по энергетическому критерию в два раза меньше, чем ширина спектра по пороговому критерию
Применение разложения в ряд Фурье, при проведении расчета прохождения сигнала через ЛЭЦ, позволило свести задачу анализа цепей при периодическом воздействии к задаче анализа цепей при гармоническом воздействии.