2. Анализ линейной электрической цепи во временной и частотной областях

1. Исходные данные

	№ варианта	№ схемы
	12	1

Рисунок 2.1 – Схема электрической цепи

(2.1)

(2.2)

2. Расчет и построение частотных характеристик аналогового фильтра

Расчет операторного выражения передаточной функции

Перейдем в комплексную плоскость заменой

Сравнивая между собой выражения и , необходимо заметить, что это не просто замена переменных , а переход со всей плоскости комплексных частот на мнимую ось .

Нормируем по

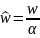
АЧХ

ФЧХ

Графическое представление АЧХ и ФЧХ

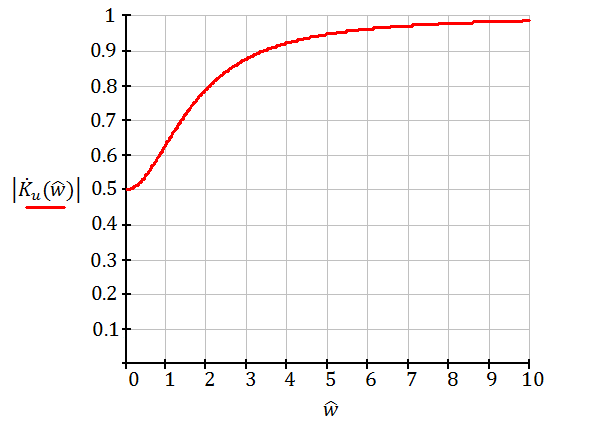
Рисунок 2.2 – АЧХ аналогового фильтра

Рисунок 2.3 – ФЧХ аналогового фильтра

3. Расчет и построение временных характеристик аналогового фильтра

Рассмотрим в качестве входных сигналов идеальные обобщенные модели: дельта-функцию и функцию Хевисайда .

Отклик линейной системы с нулевыми начальными условиями на воздействие - функции называется импульсной характеристикой .

Отклик линейной системы с нулевыми начальными условиями на воздействие единичного скачка называется переходной характеристикой .

При определении импульсной характеристики необходимо проверить,

удовлетворяет ли передаточная функция требованиям, предъявляемым к изображениям по Лапласу

(2.3)

В нашем случае из передаточной функции следует выделить целую часть.

1. Расчет импульсной характеристики

Изображение по Лапласу импульсной характеристики совпадает с передаточной функцией , т. к. изображение дельта-функции равно 1

Таким образом, импульсная характеристика и передаточная функция цепи связаны между собой прямым и обратным преобразованиями Лапласа

(2.4)

Полюсом является

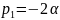
Найдем вычет

отсюда

Графическое представление импульсной характеристики

Нормируем по , заменяем

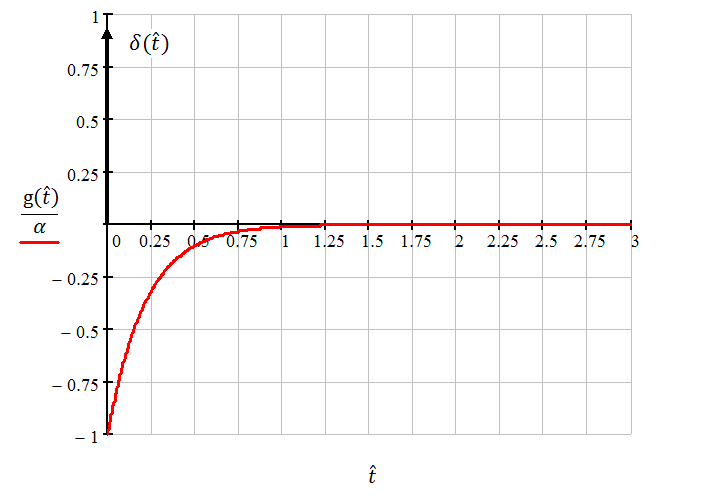
Рисунок 2.4 – Импульсная характеристика

2. Расчет переходной характеристики

Изображение по Лапласу входного единичного скачка, как раннее было рассмотрено, равно

Переходная характеристика и передаточная функция цепи связаны между собой следующим образом

(2.5)

Полюсами являются

Найдем вычеты

отсюда

Графическое представление переходной характеристики

Нормируем по

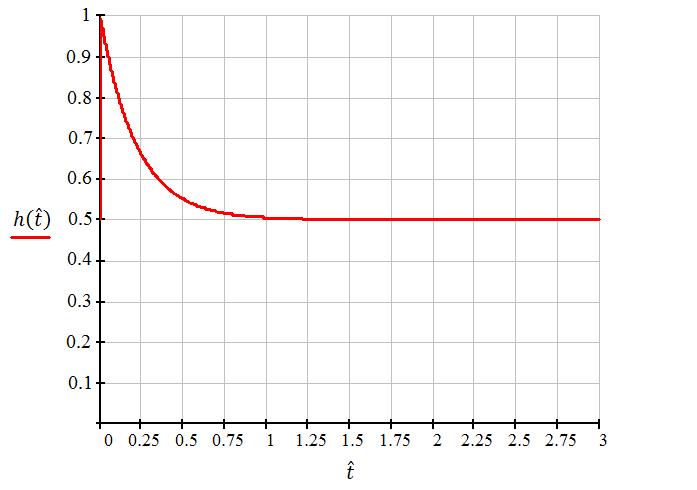
Рисунок 2.5 – Переходная характеристика

4. Анализ и проверка полученных выражений

1. Проверка операторного выражения передаточной функции на крайних частотах

Рисунок 2.6 – Заданная цепь при

Рисунок 2.7 – Заданная цепь при

2. Анализ цепи по исходным данным и полученным выражениям

Анализируя полученные передаточные функции, мы видим, что заданная цепь является фильтром верхних частот (ФВЧ) второго порядка.

3. Анализ временных характеристик

Переходная и импульсная характеристики существуют только при , так как отклики не могут опережать воздействия.

4. Cвязь между переходной и импульсной характеристиками

Переходная и импульсная характеристики связаны между собой так же, как и входные воздействия

, (2.6)

а именно

5. Предельные соотношения

(2.7)

(2.8)