1 Спектральный анализ аналоговых непериодического и периодического сигналов 7

1.1 Исходные данные 7

1.2 Разложение непериодического сигнала на типовые составляющие 7

1.3 Расчет изображения аналогового непериодического сигнала по Лапласу 8

1.4 Нахождение спектральной плотности аналогового непериодического сигнала 10

1.5 Вычисление коэффициентов комплексного ряда Фурье, описывающего аналоговый периодический сигнал 11

1.6 Расчет ширины спектра периодического сигнала по пороговому критерию 13

1.7 Представление аналогового периодического сигнала усеченным рядом Фурье аналитически и графически 14

1.8 Расчет и построение погрешности представления аналогового периодического сигнала усеченным рядом Фурье 15

2 Анализ линейной электрической цепи во временной и частотной областях 16

1.1 Исходные данные 17

1.2 Расчет и построение частотных характеристик аналогового фильтра 17

1.3 Расчет и построение временных характеристик аналогового фильтра 19

1.3.1 Расчет импульсной характеристики 20

1.3.2 Расчет переходной характеристики 21

1.4 Анализ и проверка полученных выражений 22

2 Расчет и построение отклика аналогового фильтра на сигнал 25

2.1 Расчет прохождения периодического сигнала через ЛЭЦ 25

2.2 Расчет прохождения непериодического сигнала через ЛЭЦ 26

Выводы 27

Список использованных источников 28

Приложение А 29

Приложение Б 30

Введение

Большинство сигналов имеют аналоговую природу, то есть изменяются непрерывно во времени и амплитуде и могут принимать любые значения на некотором интервале. Одним из методов обработки аналогового сигнала является спектральный анализ, который позволяет охарактеризовать частотный состав измеряемого сигнала.

Задачи спектрального анализа:

• Спектральное разложение сигнала – представление сигнала в виде суммы гармонических сигналов с различными частотами.

• Анализ спектральных компонент сигнала с целью изучения свойств сигнала.

• Обратное преобразование – получение сигнала по известному спектральному разложению.

Любое периодическое несинусоидальное колебание можно разложить в бесконечный тригонометрический ряд, состоящей из постоянной составляющей и синусоидальных составляющих различной частоты, амплитуды и фазы. Совокупность этих синусоидальных или гармонических составляющих называется частотным спектром. Тригонометрический ряд, получающийся при разложении периодических несинусоидальных колебании, называется рядом Фурье.

Курсовая работа состоит из трех частей:

– Первая часть представляет собой спектральный анализ аналогового сигнала, нахождение его спектра, разложение в ряд Фурье, нахождение необходимой полосы пропускания канала связи, по которому сигнал пройдет без значительных искажений;

– Вторая часть содержит анализ аналогового фильтра, нахождение и анализ его частотных и временных характеристик.

– В третьей последней части исследуется расчет и построение отклика аналогового фильтра на периодический и непериодический сигнал.

1 Спектральный анализ аналоговых непериодического и периодического сигналов

1. Исходные данные

Код сигнала: 12

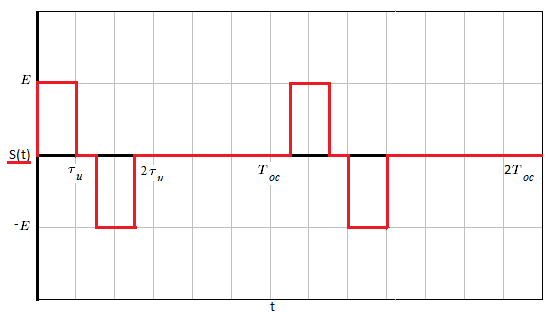
Рисунок 1.1 – Временное представление аналогового периодического сигнала

, , , (1.1)

2. Разложение непериодического сигнала на типовые составляющие

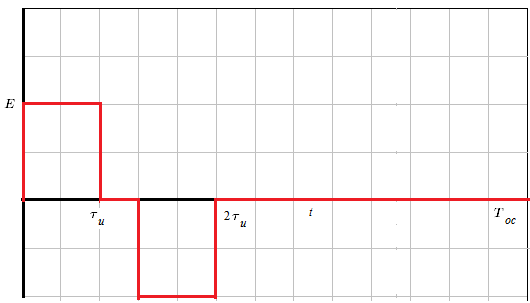
Рисунок 1.2 – Временное представление аналогового непериодического сигнала

Представление исходного сигнала с помощью элементарных составляющих, т.е. через функции Хевисайда (единичных скачков)

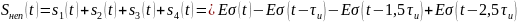
где

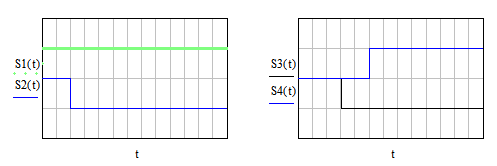
Рисунок 1.3 – Временное представление типовых составляющих аналогового сигнала

3. Расчет изображения аналогового непериодического сигнала по Лапласу

Начнем с исследования одиночного видеоимпульса. Заданный сигнал (рис. 1.1) представляет собой знакочередующуюся периодическую последовательность прямоугольных видеоимпульсов вида

Рисунок 1.4 – Одиночный прямоугольный видеоимпульс

Представим одиночный прямоугольный видеоимпульс с помощью элементарных составляющих

Найдем ее изображение по Лапласу

Непериодический сигнал (рис. 1.2) состоит из двух видеоимпульсов. Рассмотрим два знакочередующихся импульса относительно их середины

Рисунок 1.5 – Два знакочередующихся прямоугольных видеоимпульса

Из рисунка видно, что сигнал состоит из двух прямоугольных видеоимпульсов , каждый из которого сдвинут относительно оси координат, причем второй импульс находится в перевернутом положении

Согласно правилу сдвига во времени, получим

Заметим, что заданный непериодический сигнал (рис. 1.2) можно получить из сигнала (рис. 1.5), задержав его на время равное

т.е., иными словами, изображение умножается на оператор сдвига

4. Нахождение спектральной плотности аналогового непериодического сигнала

Преобразования Лапласа являются обобщениями преобразований Фурье, следовательно, спектральную плотность сигнала можно получить из изображения по Лапласу заменив на , т.е.

Преобразуем полученное выражение

Спектральная плотность является комплексной величиной. Модуль спектральной плотности аналогового сигнала называют его амплитудно- частотной характеристикой (АЧХ), аргумент спектральной плотности – фазочастотной характеристикой (ФЧХ) (см. рис. 1.6 и 1.7)

Построение частотных характеристик аналогового непериодического сигнала

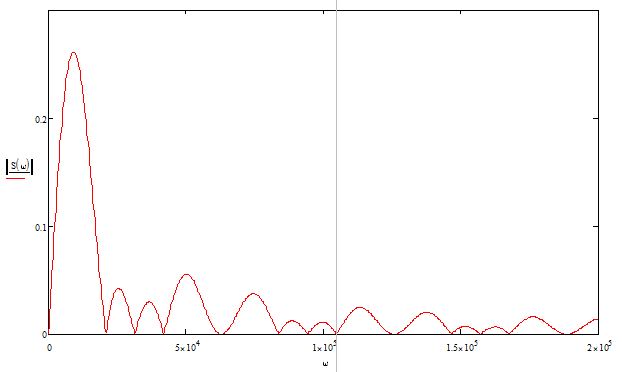
Рисунок 1.6 – АЧХ спектральной плотности

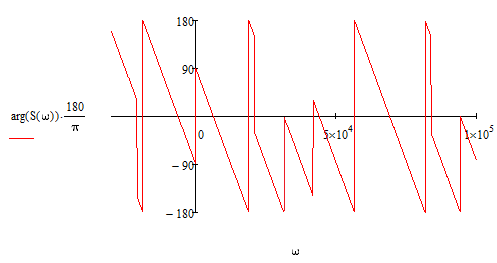
Рисунок 1.7 – ФЧХ спектральной плотности

5. Вычисление коэффициентов комплексного ряда Фурье, описывающего аналоговый периодический сигнал

Значения спектральной плотности, взятые в дискретных точках , с точностью до постоянного множителя совпадают со значениями коэффициентов

(1.4)

По формуле (1.4)

Учитывая, что , получим

Построение спектра коэффициентов комплексного ряда Фурье

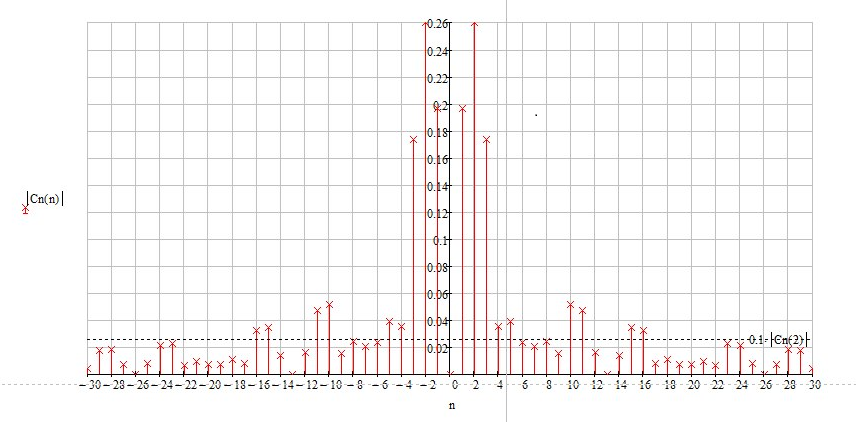
Рисунок 1.8 – Спектр коэффициентов комплексного ряда Фурье

Построение спектра фаз комплексного ряда Фурье

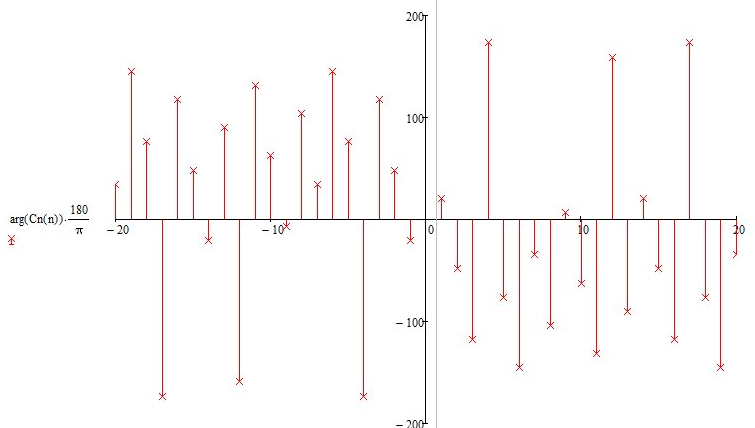
Рисунок 1.9 – Спектр фаз комплексного ряда Фурье

Положительные и отрицательные области (рис. 1.8 и 1.9) позволяют отобразить встречные направления вращения комплексных векторов .

6. Расчет ширины спектра периодического сигнала по пороговому критерию

Для ограничения спектра сигнала необходимо задаться пороговым критерием. Порог определим как десятую часть гармоники с максимальной амплитудой

Так как последний коэффициент превышающий ,

где

то сигнал соберем по 20 гармоникам, т.е. берем с запасом.

7. Представление аналогового периодического сигнала усеченным рядом Фурье аналитически и графически

Сложение гармоник приводит к образованию периодической функции с нулевым средним значением. Учитывая постоянную составляющую (ненулевое среднее значение), получим общую формулу для восстановления сигнала

(1.5)

В нашем случае

Временное представление усеченного ряда Фурье

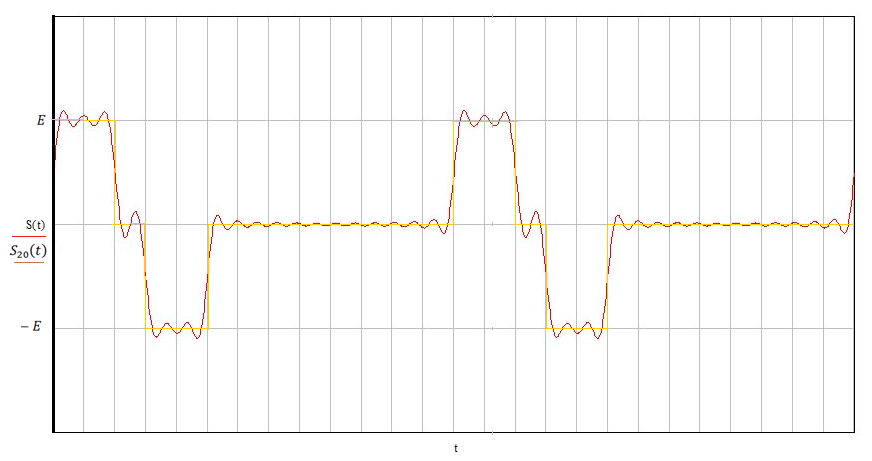
Рисунок 1.10 – Временное представление оценки из 20 гармонических колебаний

Из графика видно, что сигнал, представленный усеченным рядом Фурье, стал периодическим. Это произошло вследствие дискретизации спектральной плотности в частотной области.

В данной работе также было проведено исследование временного представления усеченного ряда Фурье в зависимости от количества гармоник (см. приложение А). При оценке из малого количества гармонических колебаний наблюдается «завал» переднего и заднего фронтов. При увеличении числа гармоник «завал» постепенно уменьшается, а временное представление усеченного ряда Фурье стремится к заданному сигналу .

8. Расчет и построение погрешности представления аналогового периодического сигнала усеченным рядом Фурье

Относительное значение погрешности аппроксимации периодического сигнала усеченным рядом Фурье определится как

(1.6)

где – средняя мощность сигнала

– средняя мощность усеченного ряда Фурье

(1.7)

Найдем средние мощности сигнала и оценки по формулам (1.7) и (1.8) соответственно

По формуле (1.6) найдем относительную погрешность аппроксимации

Найдем среднюю мощность погрешности аппроксимации (квадрат среднеквадратического значения абсолютной погрешности)

(1.9)

Анализируя поведение погрешности в зависимости от количества слагаемых ряда Фурье, можно сказать следующее: с ростом N погрешность асимптотически стремится к нулю. Кроме того, погрешность всегда положительна, т.к. мощность бесконечного ряда всегда больше мощности усеченного ряда.

Расчет ширины спектра по энергетическому критерию