Расчет ширины спектра периодического сигнала по пороговому критерию
Для ограничения спектра сигнала необходимо задаться пороговым критерием. Порог определим как десятую часть гармоники с максимальной амплитудой
– последний
коэффициент, превышающий
Представление аналогового периодического сигнала усеченным рядом Фурье аналитически и графически
Сложение
гармоник приводит к образованию
периодической функции с нулевым средним
значением. Учитывая постоянную
составляющую (ненулевое среднее
значение), получим общую формулу для
восстановления сигнала
Сигнал соберем по
20 гармоникам, т.е.
Таблица 2 – Гармонические колебания
|
|
|
|
|
|
|
0 |
|
|
|
|
-69.231 |
|
|
|
|
-138.462 |
|
|
|
|
-27.692 |
|
|
|
|
-96.923 |
|
|
|
|
-166.154 |
|
|
|
|
124.615 |
|
|
|
|
55.385 |
|
|
|
|
-13.846 |
|
|
|
|
-83.077 |
|
|
|
|
-152.308 |
|
|
|
|
-41.538 |
|
|
Временное представление усеченного ряда Фурье
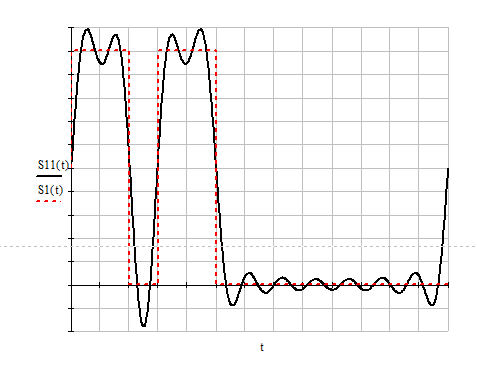
Рисунок 1.7.1 – Временное представление оценки из 11 гармонических колебаний
Расчет и построение погрешности представления аналогового периодического сигнала усеченным рядом Фурье
Относительное значение погрешности аппроксимации периодического сигнала усеченным рядом Фурье определится как
где 
– средняя мощность сигнала
– средняя мощность усеченного ряда
Фурье
Найдем средние мощности сигнала и оценки
Отсюда
Найдем среднюю
мощность погрешности аппроксимации
(квадрат
среднеквадратического значения
абсолютной погрешности)
Таблица 3 – Поведение погрешности в зависимости от количества слагаемых ряда Фурье
|
|
|
|
0 |
0.095 |
0.692 |
0.213 |
1 |
0.193 |
0.374 |
0.115 |
2 |
0.195 |
0.367 |
0.113 |
3 |
0.223 |
0.274 |
0.084 |
4 |
0.265 |
0.138 |
0.043 |
5 |
0.276 |
0.102 |
0.031 |
6 |
0.276 |
0.101 |
0.031 |
7 |
0.277 |
0.101 |
0.031 |
8 |
0.281 |
0.087 |
0.027 |
9 |
0.289 |
0.06 |
0.018 |
10 |
0.292 |
0.052 |
0.016 |
11 |
0.292 |
0.051 |
0.016 |
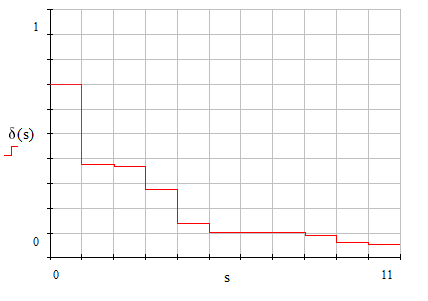
Рисунок 1.8.1 – Поведение относительной погрешности аппроксимации в зависимости от количества слагаемых ряда Фурье
Расчет ширины спектра по энергетическому критерию
