МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ

(ТУСУР)

Кафедра теоретических основ радиоэлектроники (ТОР)

СПЕКТРАЛЬНЫЙ АНАЛИЗ АНАЛОГОВЫХ СИГНАЛОВ И РАСЧЕТ ОТКЛИКОВ НА ВЫХОДЕ ЛИНЕЙНОЙ ЦЕПИ

Пояснительная записка к курсовой работе по дисциплине

«Методы Математического Описания Сигналов»

Студент группы 161

________Жамбалов Т.Б.

«___»_____________2013

Руководитель

Профессор кафедры ТОР

_________Каратаева Н.А

«___»_____________2013

2013

РЕФЕРАТ

Курсовая работа стр.26, рис., таблицы, источника.

ЗАДАНИЕ К КУРСОВОЙ РАБОТЕ

по дисциплине «Математические методы описания сигналов»

Студенту группы 161 Жамбалова Т.Б.

1. Тема работы: Спектральный анализ аналоговых сигналов и расчет откликов на выходе линейной цепи

2. Срок сдачи работы на кафедру: «8-14»_апреля_ 2013 г.

3. Цель: практическое освоение методов анализа аналоговых периодических и непериодических сигналов во временной и частотной областях, а также расчет прохождения этих сигналов через линейную цепь на примере решения конкретной задачи.

4. Рекомендуемая литература:

1. Баскаков С.И. Радиотехнические цепи и сигналы. М.: Высш. школа, 2005.-462с.(304 экз.) ISBN: 5-06-003843-2

2. Каратаева Н.А. Радиотехнические цепи и сигналы. Теория сигналов и линейные цепи. Учебное пособие. Томск: ТУСУР, 2012.-261с Режим доступа:http://edu.tusur.ru/training/publicatos/2798

3. Каратаева Н.А. Радиотехнические цепи и сигналы. Теория сигналов и линейные цепи. Учебное пособие. Томск: ТУСУР, 2003.-255с(108 экз.) ISBN 5-86889-175-9

4. Учебное методическое пособие. Радиотехнические цепи и сигналы. Часть 1. Теория сигналов и линейные цепи. Каратаева Н.А, Киселев П. Томск: ТУСУР, 2012.-33с Режим доступа:http://edu.tusur.ru/training/publicatos/2790

5. Дополнительную литературу студент ищет самостоятельно в зависимости от темы и сложности задания.

6. Задачи:

6.1. Спектральный анализ аналоговых непериодического и периодического сигналов.

6.1.1. Разложить непериодический сигнал на типовые составляющие

6.1.2. Рассчитать изображение аналогового непериодического сигнала по Лапласу

6.1.3. Найти спектральную плотность аналогового непериодического сигнала

6.1.4. Найти коэффициенты комплексного ряда Фурье, описывающего аналоговый периодический сигнал

6.1.5. Рассчитать и построить спектральные характеристики аналогового периодического сигнала.

6.1.6. Рассчитать ширину спектра периодического сигнала по пороговому критерию

6.1.7. Представить аналоговый периодический сигнал усечённым рядом Фурье аналитически и графически.

6.1.8. Рассчитать и построить погрешность представления аналогового периодического сигнала усечённым рядом Фурье

6.2. Анализ линейной электрической цепи во временной и частотной областях.

6.2.1. . Для заданной аналоговой линейной электрической цепи найти операторное выражение передаточной функции

6.2.2. Рассчитать и построить модуль (АЧХ) и аргумент (ФЧХ) комплексной передаточной функции

6.2.3 Рассчитать и построить переходную и импульсную характеристики заданной аналоговой линейной электрической цепи.

6.1.4. Рассчитать прохождение периодического сигнала через аналоговую линейную электрическую цепь (методом комплексных амплитуд). Построить отклик.

6.1.5. Рассчитать прохождение непериодического сигнала через заданную цепь (операторным или временным методом). Построить отклик.

7. Состав пояснительной записки:

7.1. Титульный лист.

7.2. Лист задания с подписью руководителя.

7.3. Содержание.

7.4. Введение. Постановка задачи.

7.5. Расчет.

7.6. Выводы по проделанной работе.

7.7. Список использованных источников.

8. Отчетность по работе:

8.1. Пояснительная записка, в обязательном порядке со всеми разделами п. 7.

8.2. После оформления пояснительной записки – защита на кафедре.

Дата выдачи задания: «11-17» февраля 2013 г.

Подпись руководителя_____________________________________Каратаева Н.А.

Подпись студента________________________________________Жамбалов Т.Б.

Оглавление

1.6 Расчет ширины спектра периодического сигнала по пороговому критерию 12

1.7 Представление аналогового периодического сигнала усеченным рядом Фурье аналитически и графически 12

1.8 Расчет и построение погрешности представления аналогового периодического сигнала усеченным рядом Фурье 14

2.1 Исходные данные 16

2.2 Расчет и построение частотных характеристик аналогового фильтра 17

2.3 Расчет и построение временных характеристик аналогового фильтра 19

2.3.1 Расчет переходной характеристики 20

2.3.2 Расчет импульсной характеристики 21

3 Расчет и построение отклика аналогового фильтра на сигнал 22

3.1 Расчет прохождения периодического сигнала через ЛЭЦ 22

3.2 Расчет прохождения непериодического сигнала через ЛЭЦ 22

Выводы 24

ВВЕДЕНИЕ

Большинство сигналов имеют аналоговую природу, то есть изменяются непрерывно во времени и амплитуде и могут принимать любые значения на некотором интервале. Одним из методов обработки аналогового сигнала является спектральный анализ, который позволяет охарактеризовать частотный состав измеряемого сигнала.

Задачи спектрального анализа:

• Спектральное разложение сигнала – представление сигнала в виде суммы гармонических сигналов с различными частотами.

• Анализ спектральных компонент сигнала с целью изучения свойств сигнала.

• Обратное преобразование – получение сигнала по известному спектральному разложению.

Любое периодическое несинусоидальное колебание можно разложить в бесконечный тригонометрический ряд, состоящей из постоянной составляющей и синусоидальных составляющих различной частоты, амплитуды и фазы. Совокупность этих синусоидальных или гармонических составляющих называется частотным спектром. Тригонометрический ряд, получающийся при разложении периодических несинусоидальных колебании, называется рядом Фурье.

Курсовая работа состоит из трех частей:

– Первая часть представляет собой спектральный анализ аналогового сигнала, нахождение его спектра, разложение в ряд Фурье, нахождение необходимой полосы пропускания канала связи, по которому сигнал пройдет без значительных искажений;

– Вторая часть содержит анализ аналогового фильтра, нахождение и анализ его частотных и временных характеристик.

– В третьей последней части исследуется расчет и построение отклика аналогового фильтра на периодический и непериодический сигнал.

1. СПЕКТРАЛЬНЫЙ АНАЛИЗ АНАЛОГОВЫХ ПЕРИОДИЧЕСКИХ И НЕПЕРЕОДИЧЕКИХ СИГНАЛОВ

1. Исходные данные

Код сигнала: 21

Рисунок 1.1.1 – Временное представление аналогового периодического сигнала

Т_ос=1300 мкс

τ_и=200 мкс

Е=1 В

ω₁=2π/T_ос

2. Разложение непериодического сигнала на типовые составляющие

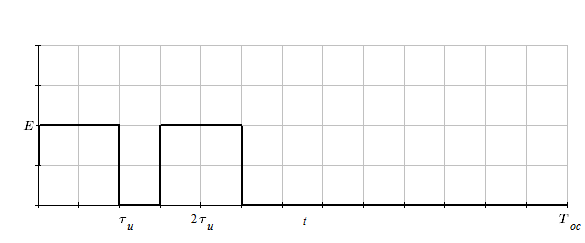
Рисунок 1.2.1 – Временное представление аналогового не периодического сигнала

Представление исходного сигнала с помощью элементарных составляющих, т.е. через функции Хевисайда:

где

Рисунок 1.2.1 – Временное представление типовых составляющих аналогового сигнала

3. Расчет изображения аналогового непериодического сигнала по Лапласу

Так как заданный сигнал (рис. 1.1.1) представляет собой периодическую последовательность видеоимпульсов, то исследуем сначала одиночный видеоимпульс

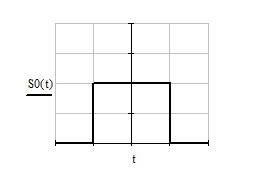
Рисунок 1.3.1 – Одиночный прямоугольный видеоимпульс

Представим одиночный видеоимпульс с помощью элементарных составляющих:

Найдем изображение по Лапласу:

Представим заданный сигнал (рис. 1.1.1) путем суммы одиночных видеоимпульсов S0(t), смещенных относительно оси Y:

Найдем изображение по Лапласу, домножая S0(t) на оператор сдвига:

4. Нахождение спектральной плотности аналогового непериодического сигнала

Заменяя оператора Лапласа p на jω, получим:

Преобразуя полученное выражение, далее получаем:

Далее, так как спектральная плотность является комплексной величиной, то на приходится работать с его модулем, который называется амплитудно-частотная характеристика(АЧХ), и аргументом, который называется фазочастотная характеристика(ФЧХ):

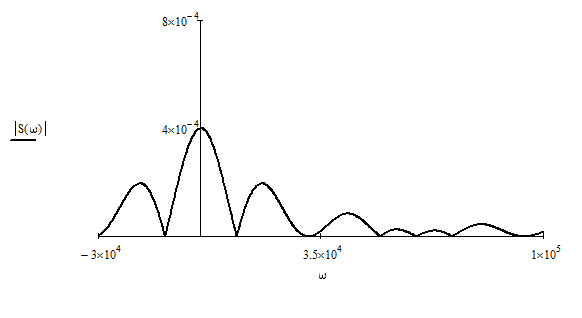
Рисунок 1.4.1 – АЧХ спектральной плотности

Рисунок 1.4.2 – ФЧХ спектральной плотности

5. Вычисление коэффициентов комплексного ряда Фурье, описывающего

аналоговый периодический сигнал

Значения спектральной плотности, взятые в дискретных точках ω=nω­­­₁,

с точностью до постоянного множителя T_ос совпадают со значениями

коэффициентов С_n

Далее, так как и , получим:

Построение спектра коэффициентов и спектра фаз комплексного ряда Фурье

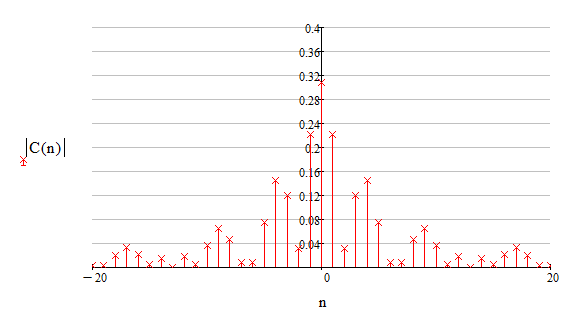
Рисунок 1.5.1 - Спектр коэффициентов комплексного ряда Фурье

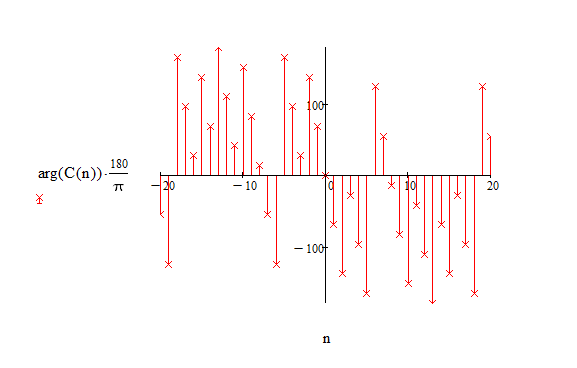
Рисунок 1.5.2 – Спектра фаз комплексного ряда Фурье

Таблица 1 – Коэффициенты комплексного ряда Фурье

n	Cn	|Cn|	Arg(Cn)
0	0.308	0.308	0
1	0.079-0.207i	0.221	-69.231
2	-0.024-0.021i	0.032	-138.462
3	0.106-0.056i	0.12	-27.692
4	-0.017-0.143i	0.144	-96.923
5	-0.073-0.018i	0.075	-166.154
6	-5.115e-3+7.41e-3i	9.004e-3	124.615
7	4.384e-3+6.352e-3i	7.718e-3	55.385
8	0.045-0.011i	0.047	-13.846
9	7.741e-3-0.064i	0.064	-83.077
10	-0.032-0.017i	0.036	-152.308
11	4.297e-3-3.807e-3i	5.741e-3	-41.538