- •Лабораторная работа № 11 интерферометр фабри-перо
- •Лабораторная работа № 12 исследование распространения свч электромагнитных волн в волноводах
- •1. Исследование волны в пустом волноводе.
- •2. Исследование волны в волноводе, заполненном диэлектриком.
- •Лабораторная работа № 13 изучение поперечных волн в нагруженной струне
- •Лабораторная работа №14 исследование частотной характеристики пьезопреобразователей
- •Пьезопреобразователь, как участок пьезоактивной среды, помещенной в электрическое поле.
- •Лабораторная работа № 15 исследование распространения света в оптически неоднородной среде
- •Лабораторная работа №16 исследование явления дифракции электронов на щели
- •1.Дифракция плоской электромагнитной волны на щели в непрозрачном экране.
- •2.Спектр амплитуд при дифракции электромагнитных волн на щели в непрозрачном экране.
- •4. Компьютерное моделирование дифракции электронов.
- •Лабораторная работа №17 волны на свободной поверхности жидкости
- •Лабораторная работа № 18 исследование дифракции фраунгофера на n щелях
Лабораторная работа №16 исследование явления дифракции электронов на щели
В лабораторной
работе предлагается провести изучение
закономерностей дифракции электронов
на плоской щели в непрозрачном экране
при компьютерном моделировании этого
процесса. Моделирование отражает
физический эксперимент, в котором
счетчиков электронов, установленных
за щелью, фиксируют число электронов
![]() ,
попавших в каждый из них за определенное
время (время экспозиции). Схема такого
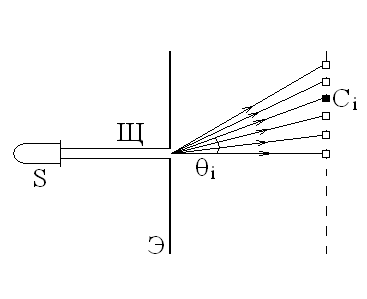
эксперимента представлена на рис 1.
,
попавших в каждый из них за определенное
время (время экспозиции). Схема такого
эксперимента представлена на рис 1.
|
Ci- счетчики электронов, S- источник электронов, Э - экран, Щ - щель. |
Рис. 1. Схема эксперимента |
Характерной
особенностью эксперимента является
тот факт, что отклонения электрона при
прохождении через щель на угол
![]() являются случайной величиной. При малом
числе электронов (малое время экспозиции)
заполнение каждого счетчика является
случайной величиной и может значительно
отличаться от закономерности, проявляющейся
при длительной экспозиции (
являются случайной величиной. При малом
числе электронов (малое время экспозиции)
заполнение каждого счетчика является
случайной величиной и может значительно
отличаться от закономерности, проявляющейся
при длительной экспозиции (![]() ).
Это означает, что факт отклонения
электрона после прохождения щели от
начального направления (
).
Это означает, что факт отклонения
электрона после прохождения щели от
начального направления (![]() )
проявляется при любом времени экспозиции,
а закономерность, соответствующая
дифракционной картине, только при
больших временах. Закономерность
дифракционной картины теоретически
реализована с использованием волновых
представлений. Прежде чем приступить
к анализу дифракции электронов с
использованием волновых представлений,
рассмотрим дифракцию электромагнитных
волн на щели в непрозрачном экране,
поскольку математическая сторона этой
задачи подобна.
)
проявляется при любом времени экспозиции,
а закономерность, соответствующая
дифракционной картине, только при
больших временах. Закономерность
дифракционной картины теоретически
реализована с использованием волновых
представлений. Прежде чем приступить
к анализу дифракции электронов с
использованием волновых представлений,
рассмотрим дифракцию электромагнитных
волн на щели в непрозрачном экране,
поскольку математическая сторона этой
задачи подобна.
1.Дифракция плоской электромагнитной волны на щели в непрозрачном экране.
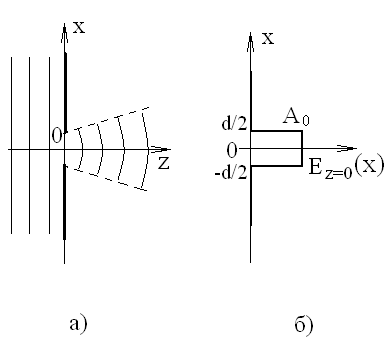
Пусть на экран со щелью падает плоская однородная гармоническая волна (рис. 2).
|
Рис. 2. Дифракция плоской электромагнитной волны на щели (а) и распределение напряженности электрического поля в плоскости щели (б). |
Амплитуда волны
во всем полупространстве (![]() )
является постоянной величиной
)
является постоянной величиной
![]() .
Уравнение этой волны в комплексной
форме можно записать в виде:
.
Уравнение этой волны в комплексной
форме можно записать в виде:
![]() (1)
(1)
Опуская множитель
![]() в (1), запишем:
в (1), запишем:
![]() (2)
(2)
После щели волновое поле напряженности становится сложным. Волна становится не плоской и не однородной, она принимает вид расходящегося "пучка". (рис.2а.)
Для описания поля
пучка в области
![]() в теории дифракции часто используют
представление о системе в этой области
однородных плоских волн с различными
волновыми векторами
в теории дифракции часто используют
представление о системе в этой области
однородных плоских волн с различными
волновыми векторами
![]() и различными амплитудами. Сумма этих
волн за счет интерференции дает
локализацию поля лишь в области пучка.
Для нашей задачи волновой вектор
изменяется в плоскости
и различными амплитудами. Сумма этих
волн за счет интерференции дает
локализацию поля лишь в области пучка.
Для нашей задачи волновой вектор
изменяется в плоскости
![]() так, что
так, что![]() .
Математически эти представления
позволяют описать поле в пучке в виде:
.
Математически эти представления
позволяют описать поле в пучке в виде:
![]() (3)
(3)
"Сумма" плоских
волн представлена интегралом и считается,
что волновой вектор
меняется непрерывно в плоскости
.
Этот вектор
имеет компоненты
![]() и
и
![]() ,
причем
,
причем
![]() ,а
,а![]() ,
где
,
где
![]() - волновое число падающей волны. Амплитуды
этих плоских волн также различны, и тоже
меняются непрерывно (у каждой волны,
заданной вектором
,
своя бесконечно малая амплитуда ).
- волновое число падающей волны. Амплитуды
этих плоских волн также различны, и тоже
меняются непрерывно (у каждой волны,
заданной вектором
,
своя бесконечно малая амплитуда ).
В этих представлениях
говорят о непрерывности спектра амплитуд
в области волновых чисел
.
Спектр определяется функцией![]() ,
который по смыслу является спектром
амплитуд волн, определяющих поле на
щели.
,
который по смыслу является спектром
амплитуд волн, определяющих поле на
щели.
![]() (4)
(4)
В математическом
отношении (4) носит название Фурье-образа
функции![]() ,
а соотношение
,
а соотношение
![]() (5)
(5)
- интегрального Фурье-преобразования функции .