Министерство образования Московской области

Московский государственный областной университет

СПЕЦИАЛЬНЫЙ ФИЗИЧЕСКИЙ ПРАКТИКУМ

Физико-математический факультет

Москва

2012

Печатается по решению ученого совета физико-математического факультета МГОУ (протокол № 2 от 18 октября 2012 г.)

Составители: Аброшина Л.С.,канд. физ.-мат. наук, доц., Башлачёв Ю.А.,канд. физ.-мат.наук,

Васильчикова Е.Н., канд. физ.-мат. наук, доц.

Рецензент: Дадиванян А.К., д-р физ.-мат. наук, проф.

АБРОШИНА Л.С., БАШЛАЧЁВ Ю.А., ВАСИЛЬЧИКОВА Е.Н. Специальный физический практикум – М.: МГОУ, 2012. – 44с.

Данное пособие предназначено для студентов направлений подготовки «Физика» и «Педагогическое образование» (профиль «Физика и информатика») физико-математического факультета МГОУ и представляет собой лабораторный практикум, основной задачей которого является формирование у студентов единого подхода к анализу волновых процессов различной физической природы.

Пособие содержит описание лабораторных работ в специальном физическом практикуме, включая краткую теорию и методические указания по выполнению экспериментальных исследований.

© Аброшина Л.С., Башлачёв Ю.А, Васильчикова Е.Н., 2012

© МГОУ, 2012

Лабораторная работа № 11 интерферометр фабри-перо

Интерферометр Фабри–Перо, использующий интерференцию плоских волн, порожденных отражением от границ раздела плоскопараллельного слоя, относится к классу спектральных приборов высокого разрешения. В интерферометре Фабри-Перо реализуется многолучевая интерференция с локализацией полос равного наклона в бесконечности (рис.1)

В конструктивном отношении интерферометр обычно представляет собой две круглые пластины, плоскость поверхности которых выдержана с высокой точностью (погрешность составляет 0.01 длины световой волны). По толщине пластины имеют форму плоского клина (для исключения интерференции внутри пластины) с малым углом (он составляет всего несколько угловых минут). Одна из плоскостей каждой пластины покрыта отражающей пленкой (алюминий, серебро, многослойный диэлектрик). Для образования интерференционного слоя между пластинами ставят распорное цилиндрическое кольцо толщиной . Кольцо в основаниях имеет по три выступа, на которые и опираются пластины зеркальными поверхностями. Эти выступы дают возможность юстировать пластины друг относительно друга с помощью пружинящих упоров до образования плоскопараллельного слоя между "зеркальными" плоскостями. Пластины вместе с распорным кольцом помещаются в светонепроницаемый кожух (цилиндр с черненой внутренней поверхностью) и фиксируются там жестко, оставляя возможность малой юстировки.

Апертура интерферометра определяется внутренним диаметром распорного кольца, который делают достаточно большим (70-80 мм), что позволяет считать интерферометр Фабри-Перо светосильным оптическим прибором. Возможность использования протяженных источников света в сочетании с линзовыми системами так же позволяет увеличить освещенность интерференционной картины. Замечательной особенностью интерферометра Фабри-Перо, по сравнению с другими спектральными приборами высокого разрешения, является его двухмерная дисперсия, так как интерференционные максимумы (минимумы) имеют форму концентрических колец (как линии равного наклона). Эту особенность можно удачно использовать при фотоэлектрическом методе регистрации спектров и при совмещении интерферометра с призменным спектрографом.

Принципиальная схема наблюдения интерференционной картины интерферометра в сочетании с простой линзовой системой приведена на рис.2. Свет от протяженного источника падает на интерферометр под различными углами. Линза не влияет на распределение интенсивности в интерференционной картине, она обеспечивает увеличение светового потока. Для наблюдения полос равного наклона плоскость экрана должна совпадать с фокальной плоскостью линзы L₂. Интерференционная картина может наблюдаться также с помощью зрительной трубы, установленной на бесконечность.

Двухмерная интерференционная картина, наблюдаемая на экране в монохроматическом свете, имеет вид концентрических окружностей.

Теория интерферометра.

В методическом отношении существуют различные подходы к рассмотрению теоретических основ интерферометра Фабри - Перо. К ним относятся: многолучевые представления (рис.1), волноводные представления с использованием неоднородных стоячих волн, метод пассивных четырехполюсников.

Рассмотрим второй подход, причем образование стоячих волн будем рассматривать как сумму плоских бегущих волн, порожденных многократным отражением. Пусть зеркальные плоскости пластин интерферометра совпадают с плоскостями и (рис.З.).

Рис.3 Образование стоячих волн в интерферометре

На границах раздела и происходят отражения волн, так что в среде будут существовать плоские волны с волновыми векторами и . Они будут интерферировать и могут породить стоячую волну с волновым числом или "погасить" друг друга. В случае образования стоячей волны, коэффициент передачи энергии волны, падающей на интерферометр, будет максимальным, что соответствует "максимуму" интерференционной картины. Итак, постановка задачи в теоретическом аспекте: задана плоская монохроматическая волна, падающая под определенным углом на интерферометр. Определить, каким условиям должен удовлетворять угол для этой волны, чтобы интенсивность прошедшей волны была максимальна. В математическом отношении - определить зависимость интенсивности прошедшей через интерферометр волны от направления . Поскольку интерференционный слой является плоскопараллельным, то направления падающей и прошедшей волны будут одинаковыми, т.е. . Будем рассматривать образование стоячей волны с волновым числом , где - волновое число волн, порожденных отражениями на границах раздела (1,2) и (2,1). Рассмотрение волны с волновым числом упрощает задачу, поскольку нужно рассматривать лишь нормальное падение волн на границу раздела. Пусть и – амплитудные коэффициенты отражения и прозрачности при переходе волны из окружающей среды в плоско параллельную пластину (в том числе, воздушный промежуток между зеркалами), и – соответствующие коэффициенты при переходе из пластины в среду.

(1)

(2)

где и - показатели преломления пластины и окружающей среды.

Коэффициенты отражения и прозрачности по энергии и равны

(3)

(4)

Отсюда следует, что и .

Если пренебречь всеми видами потерь и считать, что <<1, то образование стоячей волны будет соответствовать условию: на расстоянии укладывается целое число половин длин волн

(5)

или

, (6)

где

Поскольку (обычно порядок ), то и велико ( ), что ограничивает угловые размеры наблюдаемой области интерференции малыми углами (обычно доли угловых градусов).

Преобразуем (6) для удобства введения приближений. Обозначим номер интерференционного кольца n . тогда , где при , тогда (6) принимает вид

.

Так как , то и

, (7)

или, считая ,получим

, (8)

где .

Соотношение (8) можно обсудить следующим образом. Максимумы интенсивности волны, прошедшей через интерферометр Фабри-Перо, соответствуют угловым направлениям , удовлетворяющим (8). Или: угловые размеры максимумов интерференционных колец в проходящем свете в интерферометре определены условием (8). Обозначая угловой размер первого кольца , для углового размера -го кольца из (8) имеем:

. (9)

Данная зависимость проверяется экспериментально.

Для нахождения зависимости интенсивности проходящей волны от угла наблюдения , определим амплитуду волны как сумму амплитуд волн, последовательно проходящих через слой (рис. 1).

.

Если - амплитуда падающей волны, тогда:

первая прошедшая волна: ,

вторая прошедшая волна: , (10)

-ая прошедшая волна: ,

где и – коэффициент отражения.

Суммируя уравнения в системе (10), получим уравнение колебаний в плоскости , которые породят прошедшую результирующую волну в интерферометре. Представляя эти колебания уравнением

, (11)

можно определить как амплитуду A, так и фазовую постоянную α.

. (12)

При этом учтено, что

Соотношение (12) позволяет определить исследуемую зависимость интенсивности проходящей волны от угла наблюдения . Поскольку интенсивность волны пропорциональна квадрату амплитуды, из (12) получим:

. (13)

Из полученного соотношения (13) действительно следуют значения углов , соответствующих максимумам интерференции в виде (5) и (6). Эти углы в соответствии с (13), определены условием:

. (14)

Величина интенсивности в этих максимумах равна интенсивности падающей волны . Интерференционные кольца достаточно контрастны, поскольку интенсивность в минимумах равна:

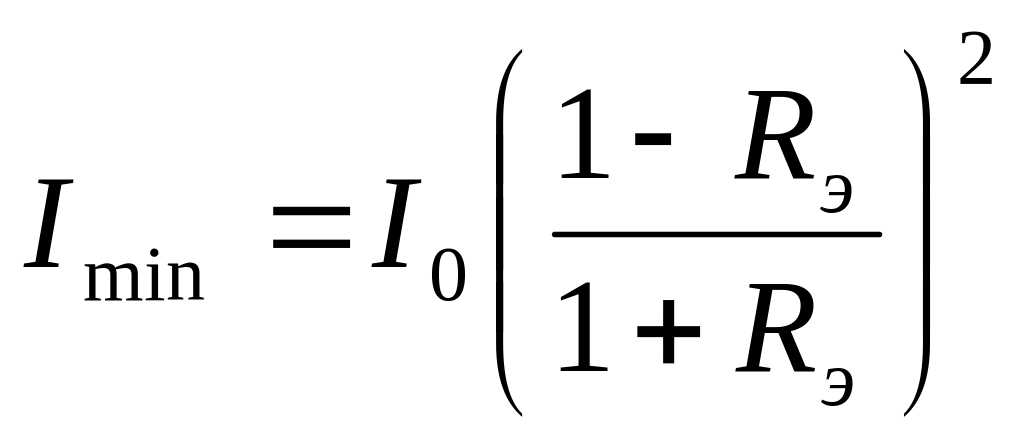. (15)

( обычно равен 0.95)

В реальных условиях (с учетом конечных размеров зеркал и различного вида потерь) контрастность значительно меньше, но характер распределения сохраняется. Используя приближения, отмеченные при получении соотношения (8), выражение (13) приводится к виду:

, (16)

где:

, , .

Соотношение (16) удобно для построения графиков при различных значениях , .

Экспериментальная установка.

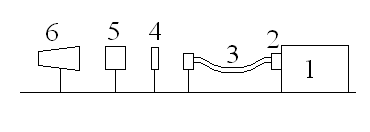
Принципиальная схема экспериментальной установки представлена на рис.4.

1 – He-Ne лазер; 2 - регулятор интенсивности пучка; 3 -волоконный световод; 4 - линза; 5 - интерферометр Фабри - Перо; 6 - зрительная труба с автоколлиматором и окулярным микрометром.

Рис.4.Схема экспериментальной установки.

Экспериментальная установка позволяет наблюдать с помощью зрительной трубы интерференционную картину интерферометра Фабри - Перо в проходящем свете. Вся система смонтирована на оптической скамье ОСК-2, что позволяет проводить необходимую юстировку и центровку отдельных частей системы. Регулировка интенсивности света от лазера осуществляется регулятором (2), представляющим собой пленочный дихроичный поляроид.

В установке использован интерферометр ИТ-30, в комплекте которого имеется стандартный набор распорных колец от 0.3 до 30 мм. Кольца малой толщины позволяют наблюдать интерференционную картину непосредственно на экране без зрительной трубы .

Задание.

1. Ознакомиться с описанием приборов, включенных в установку и подготовить установку к работе.

2. Провести наблюдение интерференционной картины в проходящем свете, выбрав наилучшие условия настройки.

3. Проведя настройку зрительной трубы "на бесконечность", провести измерения угловых размеров радиусов (диаметров) интерференционных колец, используя окулярный микрометр и (или) шкалу автоколлиматора зрительной трубы ( , где - номер кольца). Измерения провести при настройке с максимумом интенсивности в центре картины ( ).

4. По проведенным измерениям проверить соотношение (9). (Результаты представить в виде таблиц и графика).

5. Используя данные и для интерферометра провести расчет интенсивности в зависимости от значений . (Результаты представить в виде графика).

Литература.

1.Ландсберг,Г.С. Оптика [Текст] / Г.С.Ландсберг. - М.: Наука, 1976.

2.Калитеевский,Н.И Волновая оптика [Текст] / Н.И.Калитеевский. - М.: Наука, 1978.

3.Борн,М. Основы оптики [Текст] / М.Борн, Э.Вольф – М.: Наука, 1973.