4. Кінематика Основні поняття

Кінематика – розділ теоретичної механіки, у якому вивчається механічний рух об^’єкту без урахування причин, що викликають чи змінюють цей рух.

Основна задача кінематики точки:

• по заданому закону руху матеріальної точки визначити кінематичні характеристики руху точки (швидкість та прискорення).

Основна задача кінематики твердого тіла:

• по заданому закону руху твердого тіла визначити кінематичні характеристики руху тіла, а також кінематичні характеристики руху окремих точок, що належать цьому тілу.

Рівняння (закон) руху – математичні рівняння, за допомогою яких можна визначити положення матеріального об^\єкта в будь який момент часу.

Поступальний рух – рух твердого тіла, при якому довільна пряма, проведена в тілі, рухається, залишаючись паралельною своєму початковому положенню. При поступальному русі всі точки тіла рухаються однаково, тобто рухаються по однакових траєкторіях в кожну мить, з однаковими швидкостями і однаковими прискореннями. Тому законом поступального руху тіла є закон руху будь-якої його точки.

Обертальний рух навколо нерухомої осі – це рух твердого тіла, при якому точки тіла, що лежать на осі обертання, залишаються нерухомими, а всі решта точок рухаються по колах з радіусами, що дорівнюють відстані точок від осі обертання. Законом обертального руху є залежність кута повороту тіла від часу.

Поступальний і обертальний рухи тіла називають простими рухами.

Плоский рух – це рух твердого тіла, при якому всі точки тіла рухаються в площинах, паралельних деякій нерухомій площині. Задається рух будь якої точки, яка приймається за полюс, і додається закон обертання тіла навколо осі, що проходить через полюс перпендикулярно до площини руху.

Алгоритм розв’язання задач кінематики:

1. Виділити об'єкт (точку, тіло), кінематичні характеристики якого потрібно визначити.

2. Визначити вид руху, який здійснює виділене тіло.

3. Визначити кінематичні характеристики тіла або точок тіла.

Завдання к-1. Кінематика точки

Умова завдання. Точка рухається в площині (рис.К1.0-К1.9, табл.К1; траєкторія точки на рисунках показана умовно). Закон руху точки заданий рівняннями: , , де і виражені в сантиметрах, - у секундах.

Визначити. 1) Траєкторію руху точки; 2) для моменту часу визначити положення точки на траєкторії, її швидкість та прискорення , а також дотичне і нормальне прискорення і радіус кривизни у відповідній точці траєкторії.

Залежність зазначена на рисунках (рис.К1.0-К1.9), а залежність дана в табл.К1 (для рис.К1.0-К1.2 у стовпці 2, для рис.К1.3-К1.6 у стовпці 3, для рис.К1.7-К1.9 у стовпці 4).

Усі знайдені величини зобразити на рисунку.

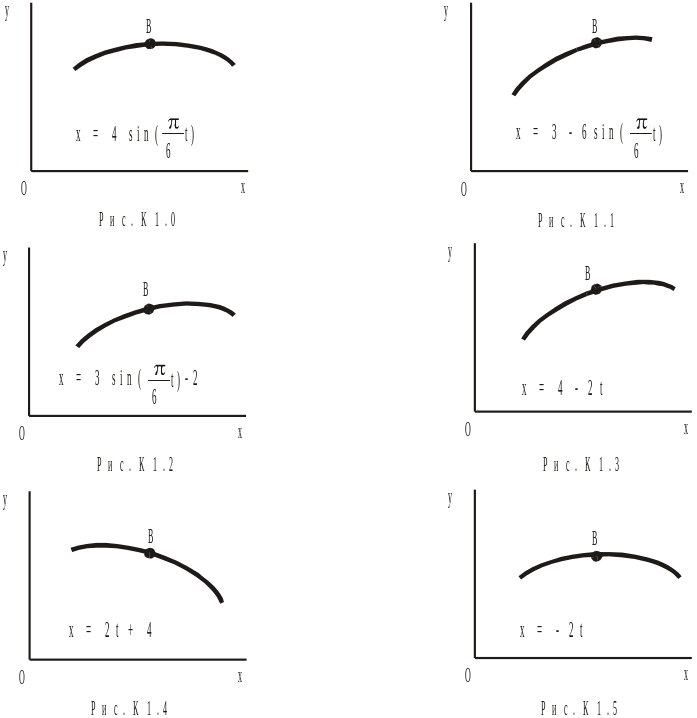
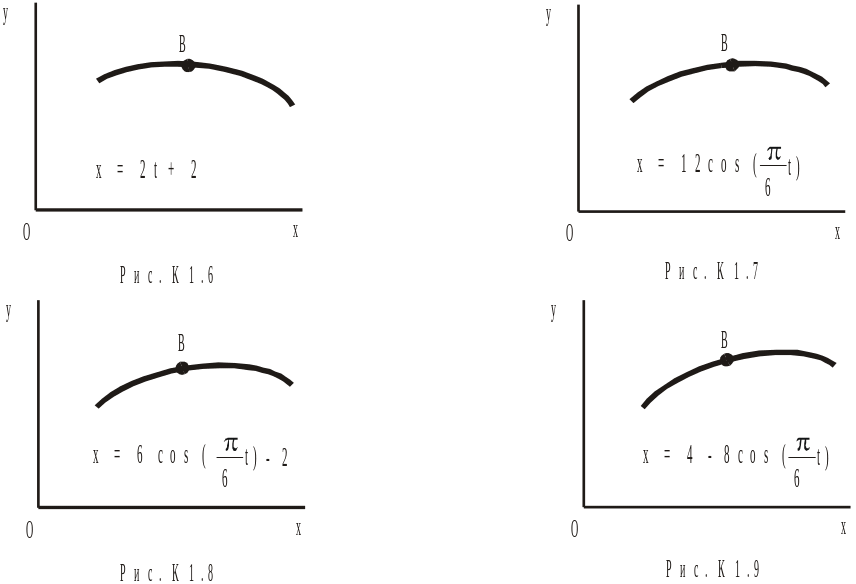
Табл.К1

Номер умови
	Рис.0-2	Рис.3-6	Рис.7-9
1	2	3	4
0
1
2
3
4
5
6
7
8
9

Теоретичне обґрунтування : [4] §36-46, [5] Разд.II, Гл. 1§.1-5, [6] Разд.2, гл.VII,§.62-65, гл.VIII, §66-68, гл.IX, § 70-77; [7]; [ 8].

Методичні вказівки. Завдання К-1 відноситься до задач кінематики точки. Тому задача зводиться до визначення траєкторії руху точки та її кінематичних характеристик (швидкості і прискорення).

Якщо рух точки відбувається у площині і заданий координатним способом, тобто , для визначення виду траєкторії необхідно виключити час з цих рівнянь і отримати залежність .^ Траєкторією руху точки є графічне відображення цієї залежності за умовою . Розрахункове положення точки – це положення точки в момент часу .

У координатному способі швидкість точки визначають по формулах:

де і - проекції вектора швидкості точки на осі нерухомої декартової системи координат .

Аналогічно визначають прискорення:

де і - проекції вектора прискорення точки на осі нерухомої декартової системи координат .

Кінематичні характеристики точки визначаються також через проекції на рухомі осі координат (осі природного тригранника). При цьому швидкість завжди буде спрямована уздовж дотичної до траєкторії осі . Вектор прискорення знаходять через його проекції на нормаль і дотичну :

,

де і .

Варто підкреслити, що незалежно від способу розкладання вектора прискорення на складові, сума проекцій повинна давати той самий вектор , що також є показником правильності отриманого результату.