- •Теоретична механіка
- •Збірник завдань та методичні вказівки до виконання розрахунково-графічних робіт
- •Маріуполь, 2012
- •Передмова
- •Вибір варіанту, рекомендації до виконання і вимоги до оформлення робіт
- •3. Статика Основні поняття
- •Основні типи в'язей. Реакції в'язей
- •Завдання с-1. Рівновага тіла під дією плоскої системи сил
- •Приклад с-1
- •Завдання с-2. Рівновага складеної конструкції під дією плоскої системи сил
- •Завдання с-3. Рівновага тіла під дією просторової системи сил
- •4. Кінематика Основні поняття
- •Завдання к-1. Кінематика точки
- •Приклад к-1
- •Завдання к-2. Кінематика простих рухів тіл
- •Завдання к-3. Дослідження плоского руху твердого тіла
- •Завдання к-4. Складний рух точки
- •5. Література
Завдання с-3. Рівновага тіла під дією просторової системи сил
Умова
завдання. Однорідна
прямокутна плита вагою
![]() зі сторонами
зі сторонами
![]() закріплена у точці
сферичним шарніром, а у точці
– циліндричним шарніром (підшипником)
і утримується в рівновазі невагомим
стержнем
закріплена у точці
сферичним шарніром, а у точці
– циліндричним шарніром (підшипником)
і утримується в рівновазі невагомим
стержнем
![]() (рис.С3.0 – С3.9).
(рис.С3.0 – С3.9).
На плиту
діють пара сил з моментом
![]() ,
що лежить у площині плити і сила
,
що лежить у площині плити і сила
![]() .
Напрямок і точка прикладання сили
зазначені у табл.С3. Точки
.
Напрямок і точка прикладання сили
зазначені у табл.С3. Точки
![]() знаходяться
всередині сторін плити.
знаходяться
всередині сторін плити.
Визначити: реакції в’язей, накладених на плиту.


Табл.С3
Напрямок сили |
|
|
|
|||
Номер рядка даних |
Точка прикладання сили |
|
Точка прикладання сили |
|
Точка прикладання сили |
|
0 |
D |
20 |
- |
- |
- |
- |
1 |
- |
- |
H |
60 |
- |
- |
2 |
- |
- |
- |
- |
E |
70 |
3 |
D |
30 |
- |
- |
- |
- |
4 |
- |
- |
H |
20 |
- |
- |
5 |
- |
- |
- |
- |
E |
30 |
6 |
D |
60 |
- |
- |
- |
- |
7 |
- |
- |
H |
30 |
- |
- |
8 |
- |
- |
- |
- |
E |
60 |
9 |
D |
70 |
- |
- |
- |
- |
Теоретичне обґрунтування : [4] § 28-29; [5] Разд. I Гл.7 § 1-7; [6] Разд.1 гл.V § 41-52; [7] ; [8]; [9]; [10].
Методичні вказівки. Завдання С-3 – на рівновагу тіла під дією просторової системи сил. Для вирішення задачі використовується алгоритм розв’язання задач статики (стор.6). Після заміни в'язей реакціями необхідно записати 6 рівнянь рівноваги в вигляді:
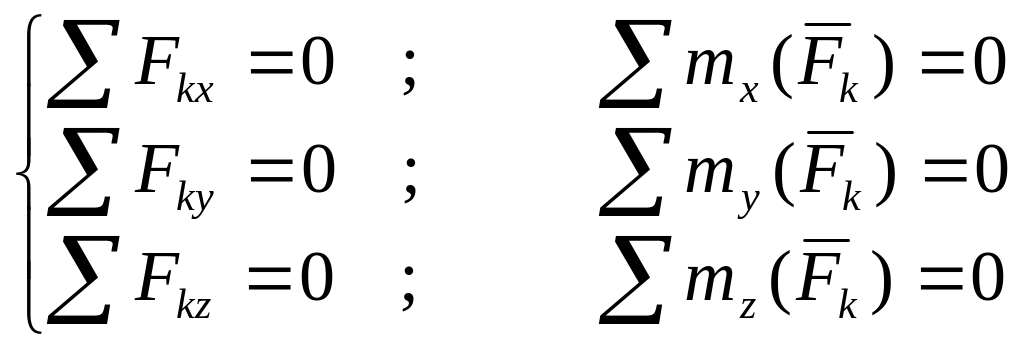 (1)
(1)
При
обчисленні моментів сил відносно осей
зручно розкласти сили на складові, які
паралельні координатним осям. Тоді по
теоремі Вариньона для кожної сили
![]() будемо мати:
будемо мати:
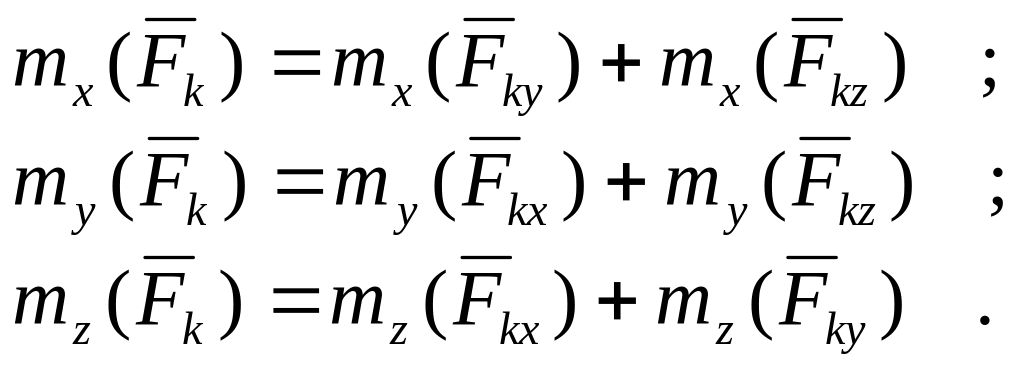 (2)
(2)
Приклад С-3
Вертикальна
прямокутна плита
![]() (рис.С3.а)
вагою
,
сторони якої
(рис.С3.а)
вагою
,
сторони якої
![]() ,
закріплена в точці
сферичним шарніром, а в точці
– циліндричним шарніром (підшипником)
і утримується в рівновазі невагомим
стержнем
,
що лежить у площині, яка перпендикулярна
осі х
.
,
закріплена в точці
сферичним шарніром, а в точці
– циліндричним шарніром (підшипником)
і утримується в рівновазі невагомим
стержнем
,
що лежить у площині, яка перпендикулярна
осі х
.
Н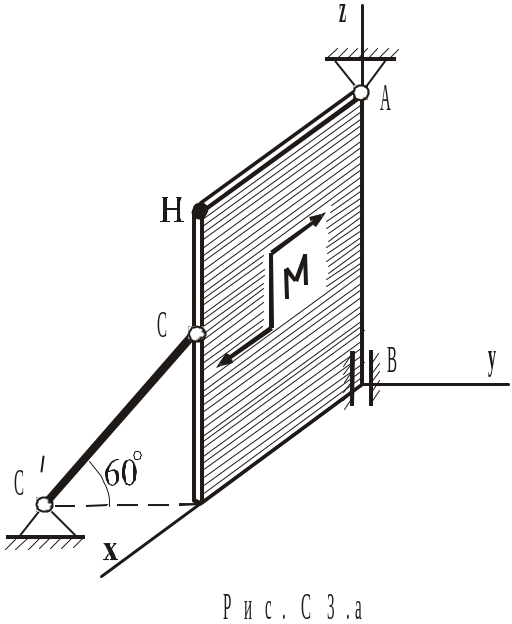 а
плиту діють пара сил з моментом
а
плиту діють пара сил з моментом
![]() ,
що лежить у площині плити і сила
,
що лежить у площині плити і сила
![]() ,
яка прикладена в точці
,
яка прикладена в точці
![]() і
лежить в площині, що перпендикулярна
осі z. Сила
спрямована
під кутом
і
лежить в площині, що перпендикулярна
осі z. Сила
спрямована
під кутом
![]() відносно додатного напрямку осі х
(якщо його відкладати
за рухом годинникової стрілки).
відносно додатного напрямку осі х
(якщо його відкладати
за рухом годинникової стрілки).
Визначити реакції в'язей плити.
Дано:

Визначити: реакції шарніру , підшипника і стержня .
Розв’язування.
Розглянемо рівновагу плити (рис.С3.а).
Зобразимо (рис.С3.б) активні сили, що діють на плиту:
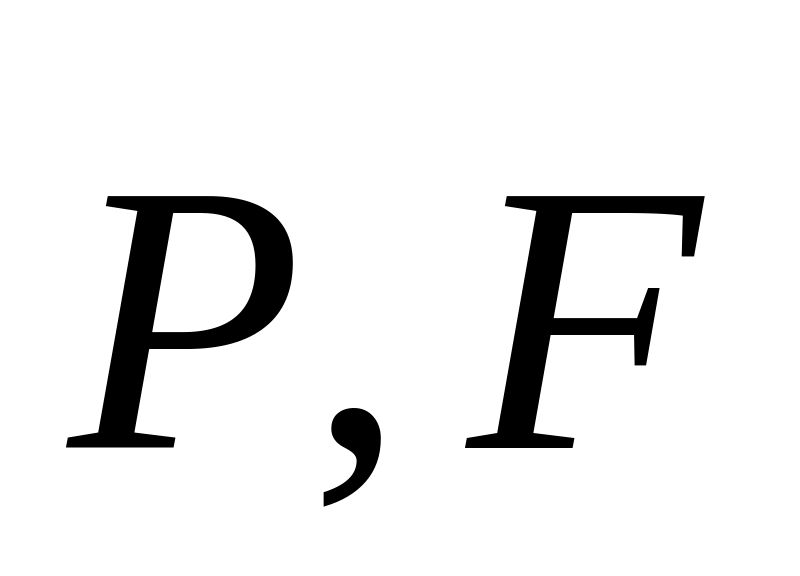 і
пару сил з моментом
.
і
пару сил з моментом
.
Н
 акладені
на плиту в'язі замінимо їх реакціями.
Реакцію сферичного шарніра
розкладемо на три складові
акладені
на плиту в'язі замінимо їх реакціями.
Реакцію сферичного шарніра
розкладемо на три складові
 ;
реакцію циліндричного шарніра
-
на дві складові
;
реакцію циліндричного шарніра
-
на дві складові
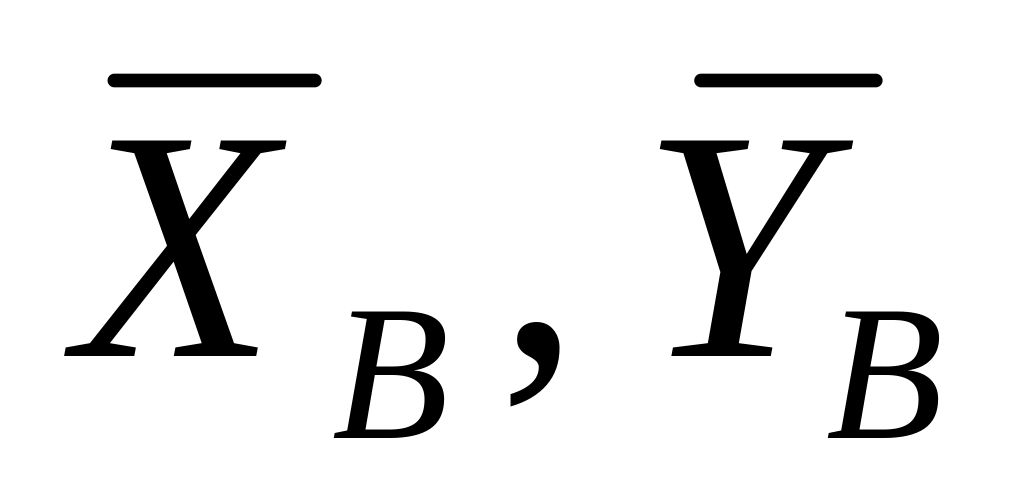 (в площині, перпендикулярній осі
підшипника); реакцію стержня
(в площині, перпендикулярній осі
підшипника); реакцію стержня
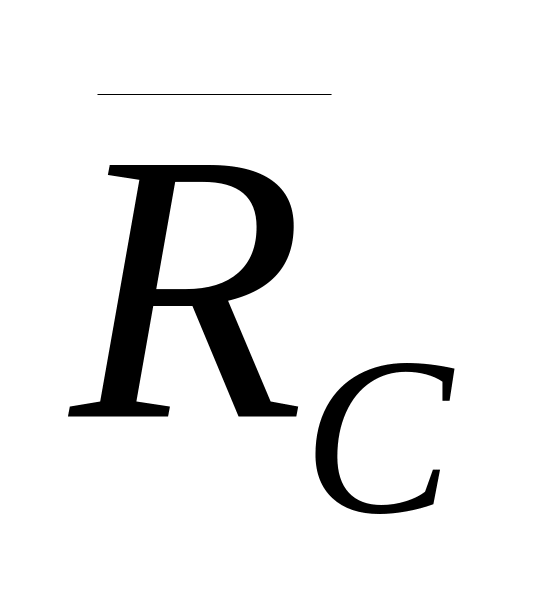 спрямуємо вздовж стержня
.
спрямуємо вздовж стержня
.
Діюча на плиту і зображена на рис.С3.б система сил є довільною просторовою зрівноваженою. Маємо 6 рівнянь рівноваги та 6 невідомих реакцій, тому задача статично означена.
Приймаємо запропоновану в умові систему координат xyz
Складемо рівняння рівноваги :
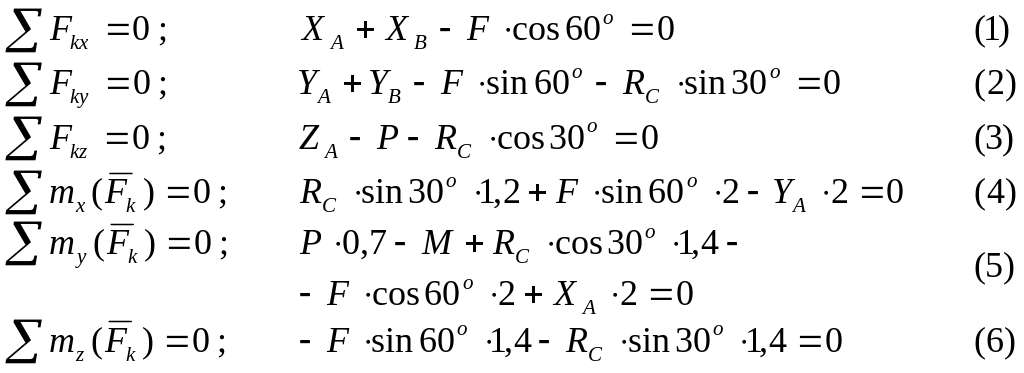
Підставимо числові значення і визначимо шукані реакції:
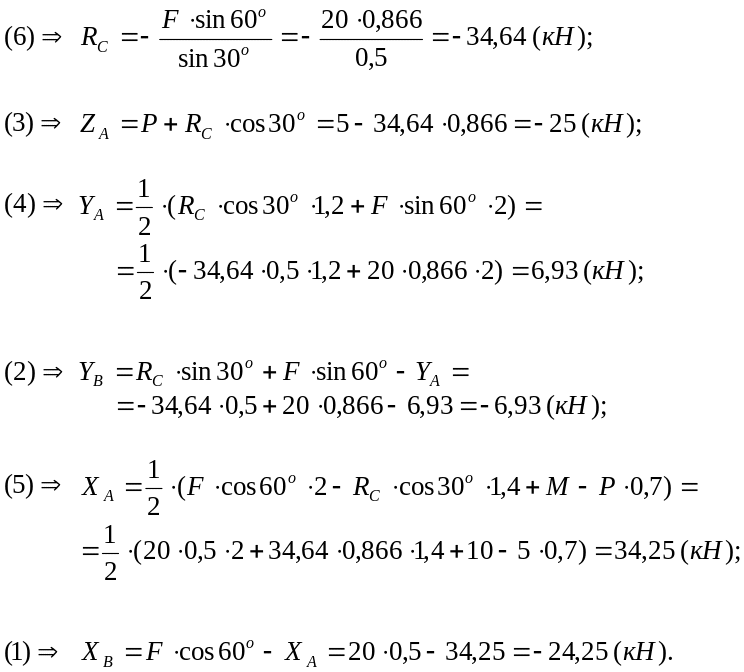

Для перевірки отриманих результатів виберемо нову систему координат
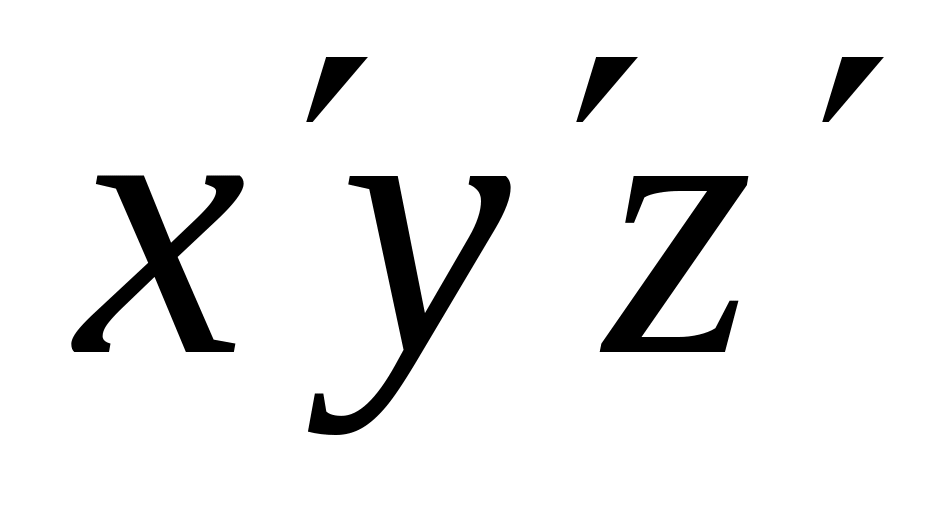 з початком у центрі ваги плити (точка
перетинання діагоналей) і з осями,
паралельними осям
з початком у центрі ваги плити (точка
перетинання діагоналей) і з осями,
паралельними осям
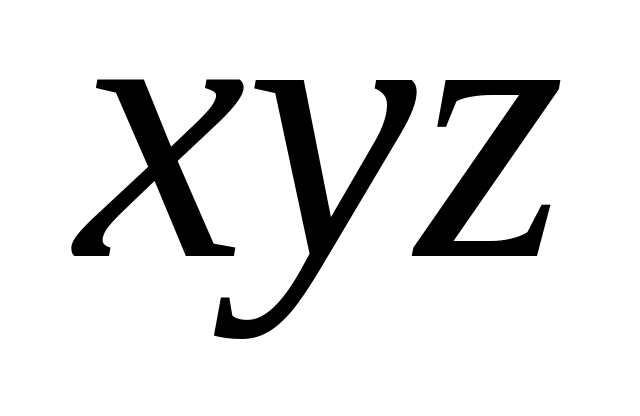 (рис.С3.в).
(рис.С3.в).
Складемо останні три рівняння рівноваги моментів сил системи щодо нових осей координат.
Отримаємо:

Таким
чином, шукані реакції знайдено вірно.
Знак « - » перед числовими значеннями
результатів указує на те, що реакції
![]() спрямовані протилежно напрямкам, які
показані на рисунку.
спрямовані протилежно напрямкам, які
показані на рисунку.
В
![]()