Завдання к-3. Дослідження плоского руху твердого тіла

Умова завдання. Плоский механізм складається зі стержнів 1, 2, 3, 4 і повзуна або (рис.К3.0 – К3.7) або зі стержнів 1, 2, 3 і повзунів і (рис.К.3.8, К3.9), з'єднаних один з одним і з нерухомими опорами , шарнірами; точка знаходиться всередині стержня . Довжини стержнів дорівнюють відповідно Положення механізму визначається кутами Значення цих кутів і інших заданих величин зазначені в табл.К3а (для рис.К3.0–К3.4) або в табл.К3б (для рис.К3.5–К3.9); при цьому в табл.К3а і - величини постійні.

Визначити. Визначити величини, зазначені в таблицях у стовпцях «Знайти». Дугові стрілки на рисунках показують, як при побудові положення механізму повинні відкладатися відповідні кути: за рухом або проти руху годинникової стрілки (наприклад, кут на рис.К3.8 варто відкласти від за рухом годинникової стрілки, а на рис.К3.9 – проти руху годинникової стрілки і т.д.).

Побудову положення механізму починати зі стержня, напрямок якого визначається кутом ; повзун з напрямними для більшої наочності зобразити так, як у прикладі К3 (рис.К3б).

Задану кутову швидкість і кутове прискорення вважати спрямованими проти руху годинникової стрілки, а задані швидкість і прискорення - від точки до (на рис.К3.5 – К3.9).

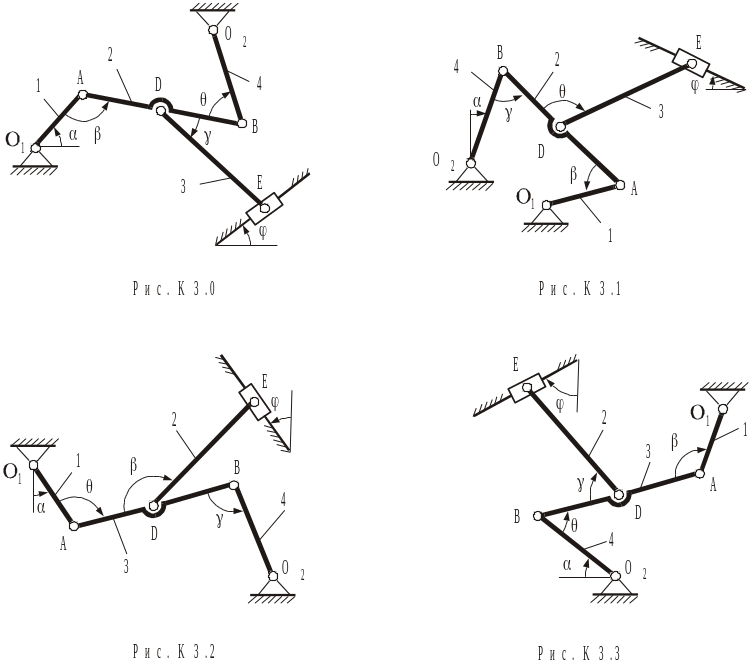
Табл.К3а

Номер умови	Кути, град					Дано		Знайти
						, рад/с	, рад/с	точок	ланки	точки	ланки
0	0	60	30	0	120	6	-	У, Е	DE	B	AB
1	90	120	150	0	30	-	4	А, Е	AB	A	AB
2	30	60	30	0	120	5	-	У, Е	AB	B	AB
3	60	150	150	90	30	-	5	А, Е	DE	A	AB
4	30	30	60	0	150	4	-	D, E	AB	B	AB
5	90	120	120	90	60	-	6	A, E	AB	A	AB
6	90	150	120	90	30	3	-	B, E	DE	B	AB
7	0	60	60	0	120	-	2	A, E	DE	A	AB
8	60	150	120	90	30	2	-	D, E	AB	B	AB
9	30	120	150	0	60	-	8	A, E	DE	A	AB

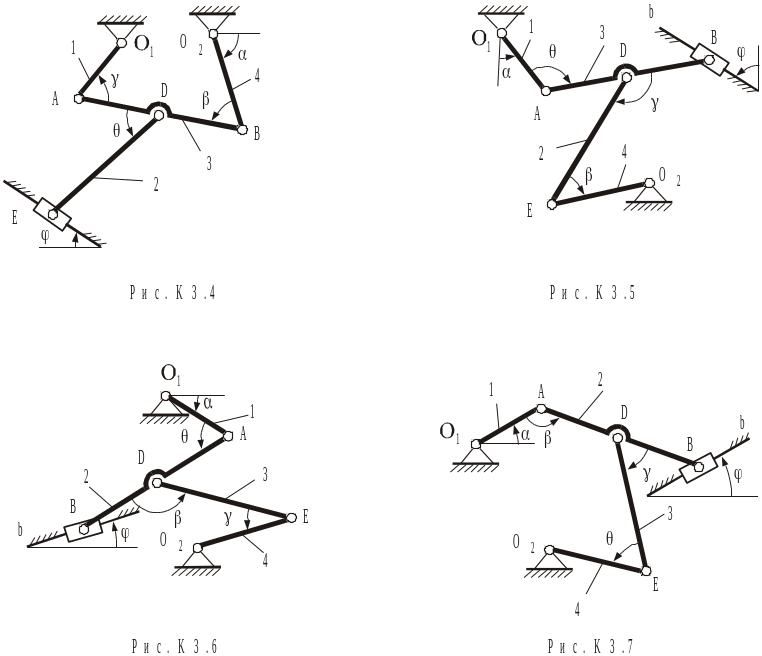
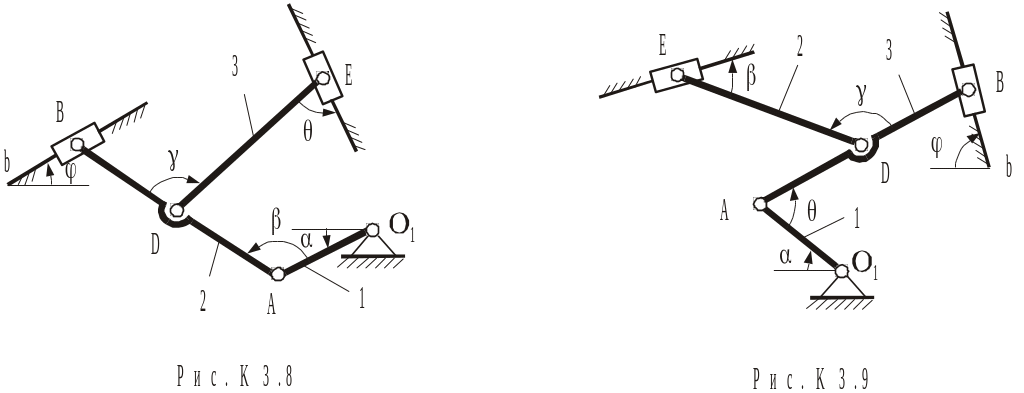
Табл.К3б

Номер умови	Кути, град					Дано				Знайти
						, рад/с	, рад/с2	, м/с	, м/с2	точок	ланки	точки	ланки
0	120	30	30	90	150	2	4	-	-	У, Е	АВ	B	AB
1	0	60	90	0	120	-	-	4	6	А, Е	DE	A	AB
2	60	150	30	90	30	3	5	-	-	У, Е	АВ	B	AB
3	0	150	30	0	60	-	-	6	8	А, Е	АВ	A	AB
4	30	120	120	0	60	4	6	-	-	У, Е	DE	B	AB
5	90	120	90	90	60	-	-	8	10	D, E	DE	A	AB
6	0	150	90	0	120	5	8	-	-	У, Е	DE	B	AB
7	30	120	30	0	60	-	-	2	5	А, Е	АВ	A	AB
8	90	120	120	90	150	6	10	-	-	У, Е	DE	B	AB
9	60	60	60	90	30	-	-	5	4	D, E	АВ	A	AB

Теоретичне обґрунтування : [4] §52-58 ; [5] Разд. II. , Гл. 3. , § 1 - 9; [6] Разд.2., Гл. XI., §85-91, §96-100; [7]; [8]; [11].

Методичні вказівки. Задача К-3 - на дослідження плоского руху твердого тіла.

Закон руху задається рівняннями:

(1)

де і - рівняння руху деякого полюса ,

- рівняння обертання тіла навколо осі, що проходить через полюс і перпендикулярна площині руху.

Відповідно до рівнянь руху (1) кінематичними характеристиками плоского руху тіла є швидкість і прискорення полюса , а також кутова швидкість і кутове прискорення тіла при його обертанні навколо осі, що проходить через полюс перпендикулярно площині руху.

Кінематичними характеристиками руху деякої точки , що належить тілу, є її швидкість і прискорення .

Швидкість будь-якої точки тіла при плоскому русі може бути знайдена:

1. векторним способом;

2. за допомогою теореми про проекції швидкостей двох точок;

3. за допомогою миттєвого центра швидкостей (МЦШ).

При векторному способі швидкість знаходять з допомогою векторного рівняння , де - швидкість полюса, а - швидкість точки в обертальному русі навколо полюса (При цьому , а ). Даний спосіб визначення швидкостей точок ще називають геометричним.

Теоремою про проекції швидкостей двох точок зручно користуватися при визначенні швидкостей точок важільних механізмів. При цьому кутове положення всіх ланок механізму щодо осей декартової системи координат повинне бути визначеним. Формулювання теореми: проекції векторів швидкостей двох точок плоскої фігури на пряму, що з'єднує ці точки, однакові. Таким чином, для будь-яких двох точок і плоскої фігури справедлива рівність: , де - кут між вектором і прямою АВ, - кут між вектором і прямою .

Миттєвим центром швидкостей (МЦШ) називають точку плоскої фігури, швидкість якої в даний момент часу дорівнює нулеві. Плоский рух тіла в даний момент часу можна розглядати як обертальний навколо МЦШ. Тому, швидкості всіх точок плоскої фігури мають величину і спрямовані так, ніби тіло виконує дійсне обертання навколо осі, що проходить через МЦШ, перпендикулярній площині плоскої фігури, тобто і . Положення МЦШ визначається точкою перетинання перпендикулярів, поставлених до швидкостей двох точок фігури (при цьому напрямки швидкостей цих точок повинні бути заздалегідь відомі). Якщо зазначені перпендикуляри виявляються паралельними і не перетинаються, то МЦШ вважають нескінченно далеким і миттєву кутову швидкість тіла – рівною нулеві. У цьому випадку рух тіла розглядається як миттєво поступальний в розумінні розподілу швидкостей, тобто швидкості всіх точок тіла однакові по величині і напрямку.

Прискорення будь-якої точки плоскої фігури може бути знайдено геометричною сумою прискорення полюса і прискорення точки при обертальному русі навколо полюса, тобто:

,

де ║ , .

Варто пам'ятати, що знайдений розподіл швидкостей і прискорень має місце тільки в даний момент часу і в даному положенні тіла. У наступний момент часу положення тіла змінюється, а разом з ним змінюються і кінематичні характеристики як самого тіла, так і його точок.

Приклад К-3

Механізм (рис.К3.а) складається зі стержнів 1, 2, 3, 4 і повзуна 5, з'єднаних шарнірами один з одним і з нерухомими опорами і . Відомо, що

(напрямки і - проти руху годинникової стрілки).

В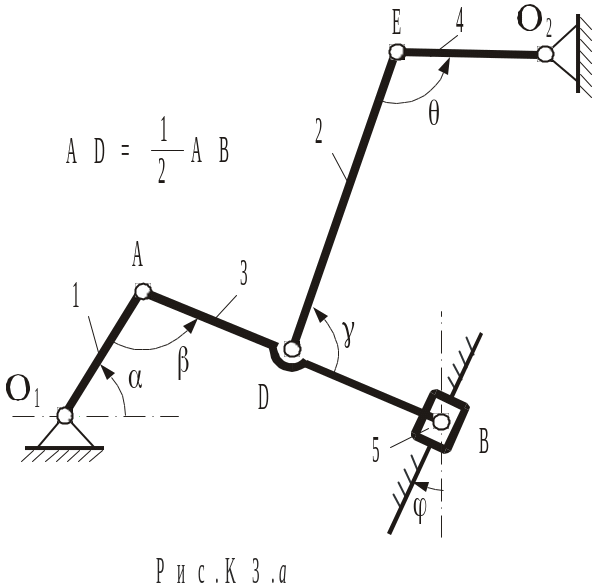 изначити величину і напрямки

Дано:

Визначити:

Розв’язування.

1. Об'єктом вивчення є весь механізм як система тіл, зв'язаних між собою (так званий кінематичний ланцюг). Величина і напрямок швидкостей і прискорень точок механізму залежать від його положення. Будуємо положення механізму відповідно до заданих кутів (рис.К3.б).

2. Визначимо швидкості точок і ланок механізму в даному положенні.

Визначення швидкостей точок і ланок починають від ланки, рух якої задано за умовою, тобто в даному прикладі - від ланки 1 (рис.К3.в).

Л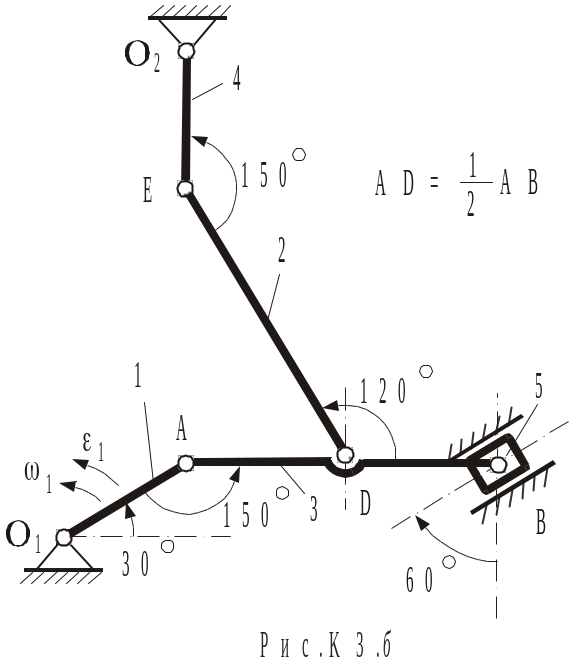 анка 1 прикріплена до нерухомого шарніру і виконує тільки обертальний, навколо нерухомої осі, рух. Точка належить ланці 1 і тому має швидкість, спрямовану перпендикулярно вбік його обертання. Величина швидкості:

(1)

Далі переходимо до наступної ланки кінематичного ланцюга - ланки 3. Ланка 3 виконує плоский рух. Точки і належать цій ланці. Швидкість точки відома по величині і напрямку. Точка належить повзуну, що рухається поступально вздовж напрямних. Таким чином, напрямок швидкості точки відомий. У цьому випадку, для визначення швидкості точки зручно скористатися теоремою про проекції швидкостей двох точок :

(2)

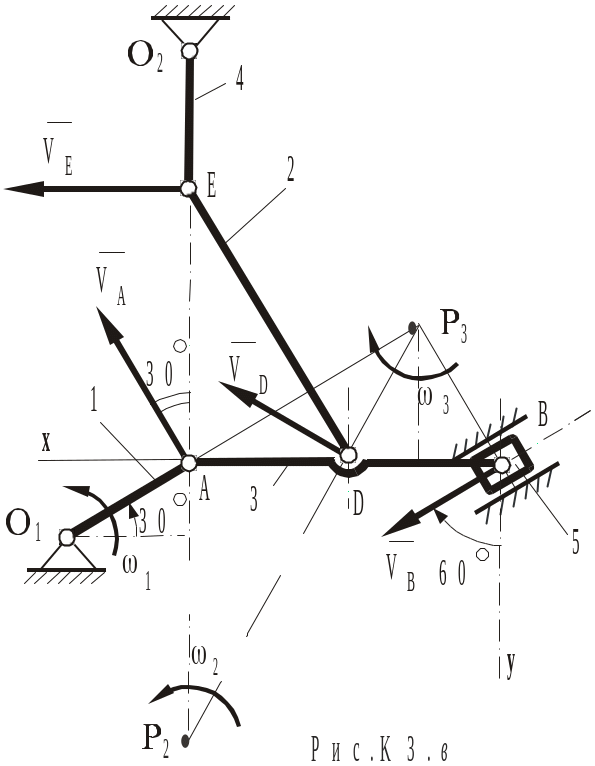З відси .

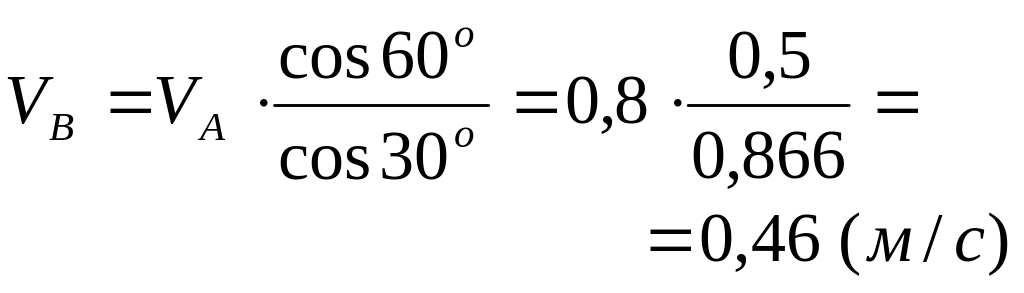Швидкість точки визначимо, використовуючи поняття про миттєвий центр швидкостей (МЦШ).^ МЦШ для ланки 3 (точка на рис.К3.в) знайдемо на перетині перпендикулярів до відомих векторів швидкостей і в точках і . Виходячи з напрямків і , визначимо напрямок кутової швидкості обертання ланки 3 навколо МЦШ. Вектор і спрямований вбік . Величину знайдемо з пропорції:

(3)

З аналізу геометричних побудов (рис.К3,в) випливає: Δ - прямокутний і Δ - рівносторонній. Таким чином, маємо:

і Тому швидкості точок і дорівнюють одна одній по величині, тобто

Визначимо кутову швидкість ланки 2 і швидкість точки . Ланка 2 виконує плоский рух. Точки і належать цій ланці. Швидкість точки відома за величиною і напрямком. Точка одночасно належить ланці 4, що обертається навколо нерухомого центра . Тому . МЦШ для ланки 2 (точка на рис.К3.в) знайдемо на перетині перпендикулярів до відомих напрямків швидкостей і в точках і . Виходячи з напрямку швидкості , визначимо напрямок кутової швидкості обертання ланки 2 навколо МЦШ. Вектор і спрямований убік . Величину знайдемо з пропорції:

(4)

З геометричних побудов випливає: , ,

Тому кутова швидкість ланки 2:

,

а швидкість точки :

.

3. Визначимо прискорення точок і ланок механізму в даному положенні.

Визначення прискорень точок і ланок починаємо від ланки, прискорення якої задано, тобто від ланки 1 (рис.К3, г).

Ланка 1 виконує обертальний рух. Точка належить ланці 1 й рухається по колові радіуса . Тоді повне прискорення являє собою векторну суму нормального і дотичного прискорень:

(5)

При цьому:

. Напрямок - уздовж до осі обертання .

. Напрямок , по напрямку .

Переходимо до наступної ланки 3. Ланка 3 виконує плоский рух. Точки і належать цій ланці. Прискорення точки відомо по величині й напрямку, тому точку зручно прийняти за полюс. Точка належить повзуну, що рухається поступально вздовж напрямних. Таким чином, напрямок прискорення точки є відомим. У цьому випадку, для визначення прискорення точки можна скористатися векторною формулою:

, (6)

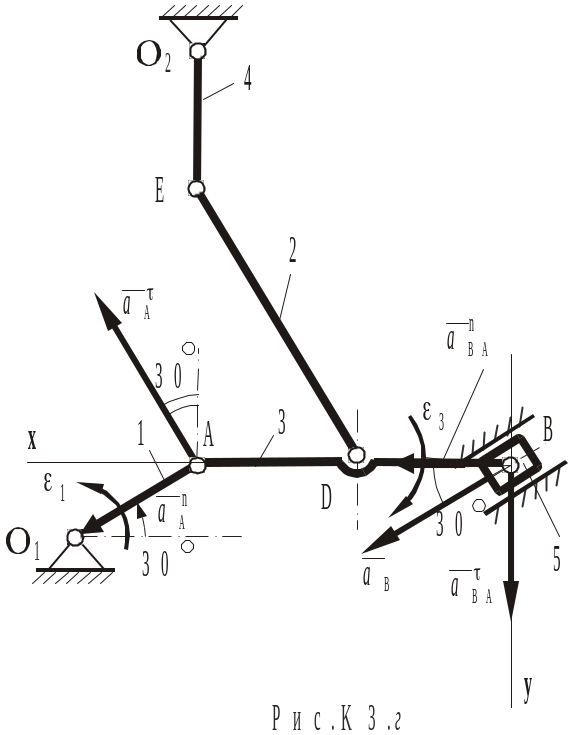д е .

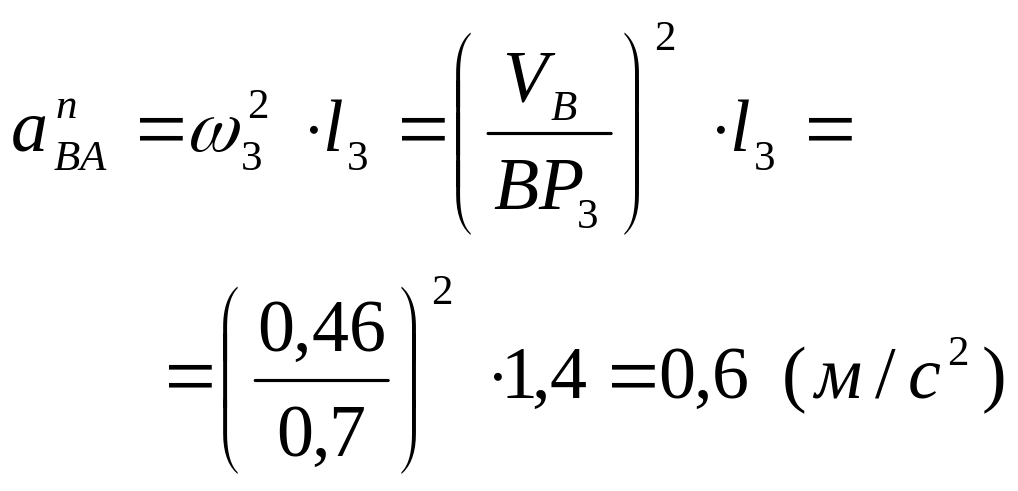Напрямок уздовж ланки , від до центра . Напрямок .

В формулі (6) двома рисками підкреслені вектора, величина й напрямок яких відомі; однією рискою – вектора, у яких відомий тільки напрямок. При наявності двох невідомих у векторнім рівнянні (6) задача їх визначення може бути розв’язана графічно або аналітично.

Визначимо величини й аналітичним методом через проекції векторного рівняння (6) на осі координат (рис.К3, г):

(7)

Підставивши числові значення в рівняння системи (7), отримаємо:

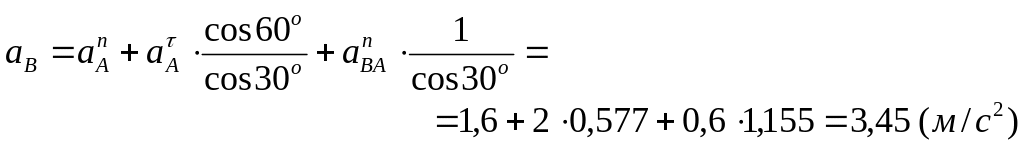
Маємо > 0 й > 0 , тому напрямок цих векторів обрано правильно.

Кутове прискорення ланки 3 визначимо з рівності:

В

ідповідь:

Примітка.

Якщо точка , прискорення якої потрібно визначити, рухається не прямолінійно, а по колові радіуса , то напрямок прискорення заздалегідь невідомий. У цьому випадку варто розкласти на дві складові й . Тоді рівняння (6) буде мати вигляд:

(8)

де ║ ; .

Далі, спроектувавши векторне рівняння (8) на осі координат, можна знайти й . Величину повного прискорення визначають за формулою:

.