Задачи регрессионного анализа:

1. Спецификация математической модели, т.е. выбор и обоснование аналитической зависимости между переменными. На этом этапе всегда получают уравнение регрессии.

В то же время, пока уравнение регрессии не будет соответствующим образом оценено, не будет проведен этап исследования его адекватности, уравнение регрессии будет представлять собой всего лишь гипотезу.

2. Статистический анализ уравнения регрессии. Этап проводится с целью определения адекватности уравнения регрессии и установления значимого влияния независимой переменной на зависимую. Этот этап называется этапом параметризации уравнения регрессии.

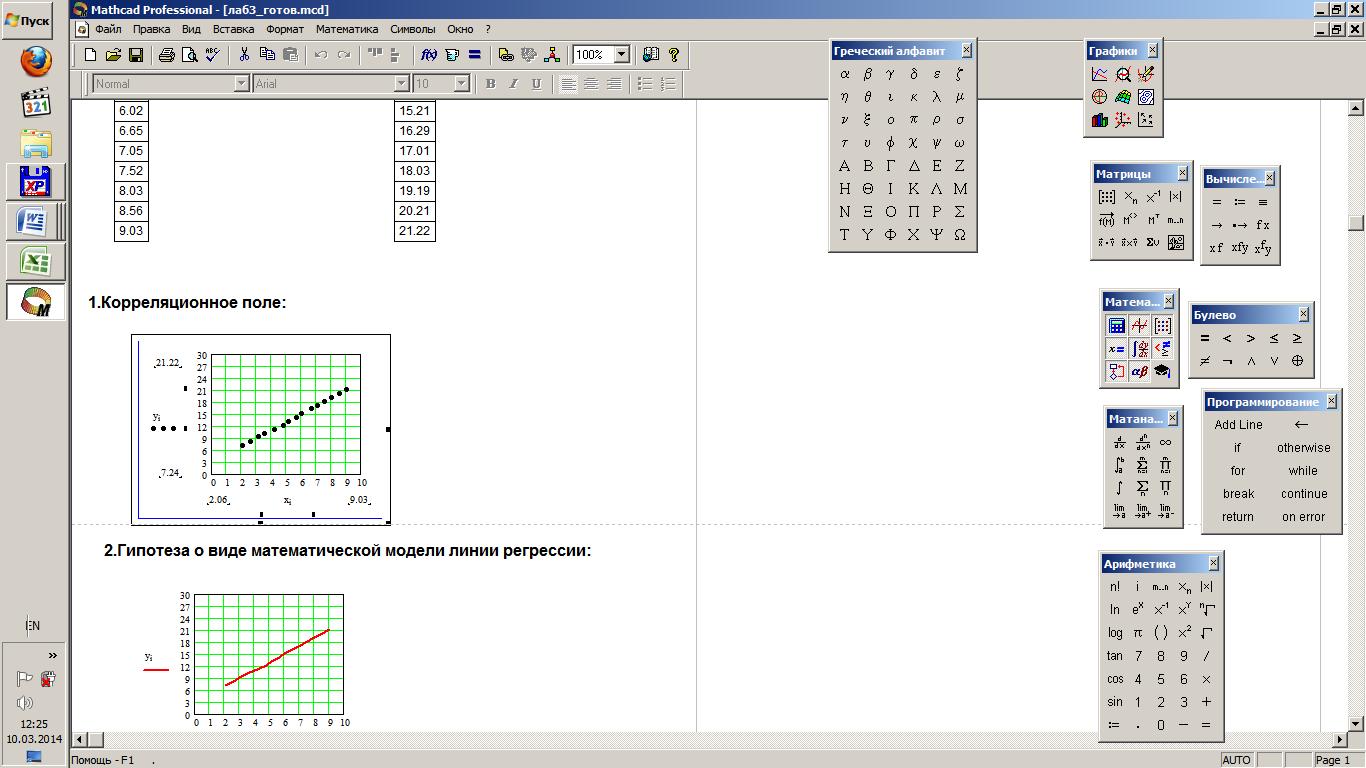
На первом этапе исследования решают задачу спецификации уравнения регрессии. Для парной регрессии такая задача решается на основе соответствующего корреляционного поля.

В зависимости от того, какое уравнение выбирается, регрессия получает соответствующее название:

y

y = a +bx

• Парная линейная регрессия

а) y =bx+a

коэффициент регрессии b положительный

x

А так же парные нелинейные регрессии:

Парная линейная регрессия

I. Метод наименьших квадратов (мнк)

Исходным пунктом экономического анализа между соответствующими переменными обычно являются оценки линейной зависимости между переменными. Если имеется некоторое облако точек, то через него можно провести такую прямую, которая наилучшим образом описывает функциональную зависимость между х и y.

В этой связи, вводят понятие критерия близости теоретической линии (описываемой уравнением регрессии) и наблюдаемыми значениями.

Как правило, такой критерий оценивает меру расстояния от наблюдаемых значений до линии регрессии.

Обычно в качестве такого критерия близости используют минимум суммы квадратов отклонений наблюдаемых переменных y_i и теоретических z_i, вычисленных по уравнению регрессии, т.е. суммы квадратов величин:

y₁

z₂

z_i

z₁

y₂

Таким образом, критерий может быть записан:

Здесь х_i и y_i — известные данные наблюдений, а а и b — параметры уравнения регрессии, подлежащие определению.

Заметим, что поскольку функция Q непрерывна, выпукла вниз и ограничена снизу нулями, то для нее будет существовать экстремум min. Вполне очевидно, что для этих экстремальных точек значения параметров a и b будут наилучшим образом описывать уравнение регрессии.

В этой связи, задача дальнейших исследований состоит в том, чтобы выявить наиболее удобные и практичные формулы для вычисления значений a и b.

Метод оценивания параметров линейной регрессии, min-ий сумму квадратов отклонений наблюдаемых значений от искомой линии называют методом наименьших квадратов. По данному методу наилучшая прямая всегда существует.

II. Оценка коэффициентов парной линейной регрессии

Предполагают, что связь между x и y линейна, т. е. . Здесь имеется в виду то, что существует связь для переменных генеральной совокупности.

Однако наличие существующих возмущений, учтенных и неучтенных фактов, а также, принимая во внимание изменчивость статистических наблюдений параметров, на практике имеют:

В этой связи задача может быть сформулирована следующим образом — по имеющимся наблюдениям факторов оценить параметры , обеспечивая при этом min величины критерия Q.

В то же время, если а является оценкой параметра , а b — параметр , то оцениваемое уравнение регрессии будет преобразовано в вид:

При этом рассмотрим процедуру оценивания а и b парной линейной регрессией.

В соответствии с МНК критерий близости будет выражен:

Для данной функции двух независимых переменных необходимое условие существования экстремума, т. е.:

В точке стационарности частные производные должны обращаться в 0.

Представленную систему представим в более удобной для анализа форме:

(1)

(2)

Проанализируем соотношение вида (1).

Обе части уравнения разделим на n.

С учётом того, что

уравнение (1) можно представить в виде:

или в более удобном виде:

(3)

Таким образом линия регрессии проходит через точку со средними значениями x и y .

Вполне очевидно, что из (3) соотношения имеют:

— оценка свободного члена линии регрессии (4)

Тогда для нахождения значения параметра b необходимо а из соотношения (4) подставить в выражение (2).

Записывая это выражение в более удобном для анализа виде, имеют:

Определяя из последнего соотношения b, имеют:

(5)

Соотношения (4) и (5) позволяют получить параметры а и b линии регрессии. При этом, будет решена первая задача исследования, а именно задача спецификации уравнения регрессии.