Этапы проверки статистических гипотез:
1. Формулируется нулевая (проверяемая) гипотеза Н0 и альтернативная гипотеза Н1;
2. Выбирается статистический критерий К и его статистика Z;
3. Вычисляется наблюдаемое (рассчётное) значение критерия Кнабл. (статистики Z) при условии, что верна Н0;
4. В зависимости от уровня значимости по соответствующим таблицам находят критическое значения критерия (Ккр.);
5. Сравнивают наблюдаемое и критическое значение соответствующего критерия (сравнивают статистики), после чего делают вывод относительно соответствующей гипотезы.
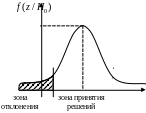
Например, если Кнабл. < Ккр., (рис.1)то гипотеза Н0 верна.
Если же Кнабл. > Ккр, (рис.1)— гипотеза Н0 неверна.
Доверительные интервалы
Ранее обсуждались вопросы исследования выборочных значений соответствующих оценок СВ. Вполне очевидно, что на этом этапе исследований получали точечные оценки соответствующих параметров и они не могут ответить на вопрос относительно степени близости выборочных значений и истинных значений параметров.
В этой связи необходимо отметить, что более содержательные процедуры оценивания параметра связаны не с точечными, а с интервальными оценками.
При этом соответствующий интервал должен накрывать оцениваемый параметр с известной степенью достоверности. В этой связи и прибегают к понятию интервальных оценок.
Интервальная оценка — оценка, которая определяется двумя числами - границами интервала, содержащего оцениваемый параметр.
Необходимо отметить, что к интервальному оцениванию прибегают, прежде всего, при малых объемах исследуемых выборок.
Заметим, что теоретическое значение оцениваемого параметра является величиной не случайной, а в тоже время его оценка является случайной величиной и изменяется от выборки к выборке. Такое обстоятельство означает, что соответственная оценка является функцией случайной величиной х1, х2, х3, ..., хn.
Допустим, оценка
параметра Q
может быть представлена как
,
тогда на основании соответствующих
наблюдений определяют две случайные
величины.
Отметим, что
соответствующий интервал
и
с заданной вероятностью В
накрывают неслучайное значение истинного
параметра
.
Заметим, что концы интервалов
и
,
как правило, находят по точечной оценке
Q.
Обычно здесь используется соотношение
вида:
Иногда Е могут быть одинаковыми или различными.
Заметим, что
утверждение, что для параметра Q совершена
интервальная оценка, означает
,
т.е. что для данного интервала, выбранного
из множества интервалов, вероятность
содержать параметр Q
соответствует величине В.
Модель линейной регрессии
Проблема оценивания экономических переменных (проблема взаимосвязи экономических показателей) является одной из важнейших проблем экономического анализа.
Любая экономическая политика заключается в регулировании экономических показателей, и эта политика должна основываться на пониании того, как эти показатели влияют на другие переменные.
Вполне очевидно, что в рыночной экономике нельзя регулировать темп инфляции. В то же время на темп инфляции можно соответствующим образом воздействовать. Например, при помощи средств бюджетно-налоговой политики, кредитно-финансовой политики. Таким образом, становится вполне очевидно, что одни экономические переменные соответствующим образом воздействовать на другие.
Учитывая указанные обстоятельства, необходимо изучать функции предложения денег и уровня цен.
Можно отметить, что вся сфера экономических исследований в определенном смысле может быть охарактеризована как изучение взаимосвязей экономических переменных.
Инструментом для базового анализа взаимосвязи экономических переменных служат методы математической статистики и эконометрии.
Наиболее простой подход к изучению экономических переменных состоит в исследовании взаимовлияния двух переменных (х и y).
Такой подход, с одной стороны, несколько упрощает математические выкладки, а с другой стороны, позволяет в достаточно удобной форме получить соответствующие геометрические интерпретации.
Можно указать 2 типа взаимосвязи х и y.