Уравнения задачи спецификации:

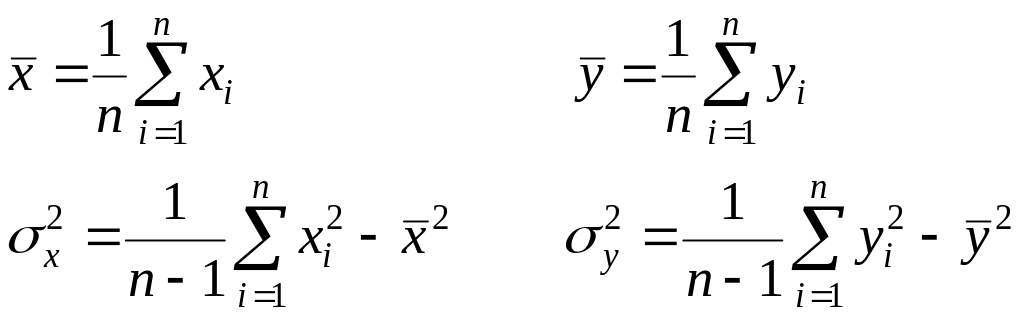
Оценка адекватности математической модели

Необходимо иметь ввиду, что пока количественно не будут оценены параметры регрессии и не будет выполнена процедура проверки сделанных оценок, форма линии регрессии остается гипотезой.

Оценка значений параметров выбранной формы уравнения регрессии называется процессом параметризации уравнения регрессии.

Однако следует иметь ввиду (на I этапе) необходимо выполнить анализ полученного уравнения регрессии.

Например, исследуя функцию спроса на телятину в одной из европейских стран, получено следующее уравнение регрессии: y = 1,2 – 1,3 ∙ x.

Полученное уравнение спроса на телятину как функция цены телятины показывает, если предположить, что при прочих равных условиях цена на телятину возрастет на 1%, то спрос на нее упадет на 1,3%.

Исследование коэффициента корреляции

Коэффициент корреляции используется в качестве меры для степени линейной связи между двумя переменными.

1. Чем ближе значение коэффициента корреляции к 1, тем теснее будет линейная связь между переменными х и y.

2. Если r > 0 - прямая регрессии возрастающая (положительная регрессия), если r < 0 - прямая регрессии убывающая (отрицательная регрессия).

3. Коэффициент корреляции может принимать значения от (-1) до (+1):

-1 ≤ r ≤ +1 .

4. Близкая к 0 величина коэффициента корреляции говорит об отсутствии линейной связи между переменными. Заметим, что здесь речь идет не вообще об отсутствии связи между переменными, а лишь об отсутствии линейной связи.

В этом случае может быть два случая:

- зависимости между факторами нет вообще;

- зависимость есть, и может быть даже очень тесная, но она не линейная.

При этом, необходимо говорить не о независимости этих переменных в данный период, а попытаться построить их более сложную связь, учитывающую как нелинейность самой этой независимости, так и инерционность динамики соответствующих величин.

В анализе коэффициента корреляции возникает следующий вопрос: если он равен 0 для генеральной совокупности, то это не значит, что он будет = 0 и для выборочной совокупности (и наоборот).

Тогда, чем больше отклонение такого параметра, тем меньше оно вероятно для соответствующей выборки. Заметим, что выборочный коэффициент корреляции является величиной случайной, тогда необходимо использовать соответствующий критерий для анализа таких оценок.

Для анализа выборочного коэффициента корреляции (статистический анализ) используют t-статистика Стьюдента.