5.1.2. Методы многомерного шкалирования

В дальнейшем развитие методов психосемантики шло по линии разработки удобных пакетов прикладных программ, основанных на методах многомерного шкалирования (МШ), факторного анализа, а также специализированных мето­дов (статистической) обработки репертуарных решеток [Франселла, Баннистер, 1987]. Примерами пакетов такого типа являются системы KELLY [Похилько, Страхов, 1990], MADONNA [Терехина, 1988], MEDIS [Алексеева, Воинов и др., 1989]. С другой стороны, специфика ряда конкретных приложений, прежде все­го в инженерии знаний, требовала также развития иных (не численных) мето­дов обработки психосемантических данных, использующих - в той или иной форме - парадигму логического вывода на знаниях. Ярким примером этого на­правления служит система AQUINAS [Boose et al., 1989; Boose, 1990]. Однако анализ практического применения систем обоих типов к задачам инженерии знаний приводит к выводу о несовершенстве имеющихся методик и необходимости их развития в соответствии с современными требованиями инженерии зна­ний. Наибольшие перспективы в этой области, по-видимому, у методов много-мерного шкалирования).

Многомерное шкалирование (МШ) сегодня - это математический инструментарий, предназначенный для обработки данных о попарных сходствах, связях или отношениях между анализируемыми объектами с целью представления этих объектов в виде точек некоторого координатного пространства. МШ представ­ляет собой один из разделов прикладной статистики, научной дисциплины, разрабатывающей и систематизирующей понятия, приемы, математические методы и модели, предназначенные для сбора, стандартной записи, систематизации и обработки статистических данных с целью их лаконичного представления, ин­терпретации и получения научных и практических выводов. Традиционно МШ используется для решения трех типов задач:

1. Поиск и интерпретация латентных (то есть скрытых, непосредственно не на­блюдаемых) переменных, объясняющих заданную структуру попарных рассто­яний (связей, близостей).

2. Верификация геометрической конфигурации системы анализируемых объек­тов в координатном пространстве латентных переменных.

3. Сжатие исходного массива данных с минимальными потерями в их информа­тивности.

Независимо от задачи МШ всегда используется как инструмент наглядного представления (визуализации) исходных данных. МШ широко применяется в исследованиях по антропологии, педагогике, психологии, экономике, социологии [Дэйвисон, 1988].

В основе данного подхода лежит интерактивная процедура субъективного шка­лирования, когда испытуемому (то есть эксперту) предлагается оценить сходство между различными элементами П с помощью некоторой градуированной шкалы (например, от 0 до 9, или от -2 до +2). После такой процедуры аналитик распола­гает численно представленными стандартизованными данными, поддающимися обработке существующими пакетами прикладных программ, реализующими раз­личные алгоритмы формирования концептов более высокого уровня абстракции и строящими геометрическую интерпретацию семантического пространства в ев­клидовой системе координат.

Основной тип данных в МШ - меры близости между двумя объектами (i, j) -dij. Если мера близости такова, что самые большие значения dij соответствуют парам наиболее похожих объектов, то dij - мера сходства, если, наоборот, наиме­нее похожим, то dij - мера различия.

МШ использует дистанционную модель различия, используя понятие расстоя­ния в геометрии как аналогию сходства и различия понятий (рис. 5.3).

Для того чтобы функция d, определенная на парах объектов (а, b), была евклидо­вым расстоянием, она должна удовлетворять следующим четырем аксиомам:

d (a,b)>0,

d(a,a) = 0,

d(a,b) = d(b,a),

d(a,b)+d(b,c) > d(a,c).

Тогда, согласно обычной формуле евклидова расстояния, мера различия двух объектов i и j со значениями признака k у объектов i и j соответственно X_ik и X_jk:

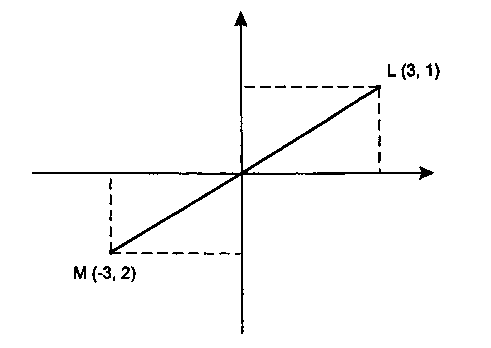
Рис. 5.3. Расстояние в евклидовой метрике

Дистанционная модель была многократно проверена в социологии и психологии [Monahan, Lockhead, 1977; Петренко, 1988, Шмелев, 1983], что дает возможность оценить ее пригодность для использования.

В большинстве работ по МШ используется матричная алгебра. Геометрическая интерпретация позволяет представить абстрактные понятия матричной алгебры в конкретной графической форме. Для облегчения интерпретации решения за­дачи МШ к первоначально оцененной матрице координат стимулов X применя­ется вращение

Среди множества алгоритмов МШ широко используются различные модифика­ции метрических методов Торгерсона [Torgerson, 1958], а также неметрические модели, например Крускала [Kruskal, 1964]

При сравнении методов МШ с другими методами анализа, теоретически приме­нимыми в инженерии знаний (иерархический кластерный анализ [Дюран, Оделл, 1977] или факторный анализ [Иберла, 1980]), МШ выигрывает за счет возможно­сти дать наглядное количественное координатное представление, зачастую более простое и поэтому легче интерпретируемое экспертами.