Задача целочисленного программирования (зцп)
Математическая модель задачи:
Областью допустимых решений (ОДР) ЗЦП является система точек, т.е. ОДР - не является выпуклой областью.
B – нецелочисленное решение
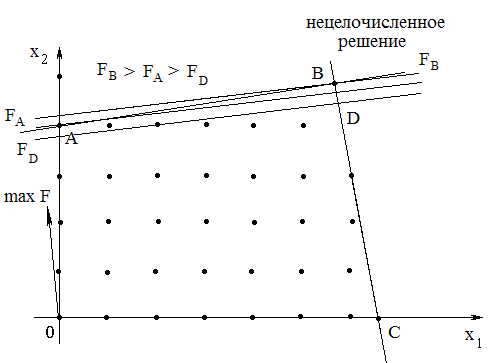
D – решение, полученное отбрасыванием дробной части
A – оптимальное целочисленное решение
Метод Гомори
Идея метода – переход к новой оптимизационной задаче с дополнительно вводимыми «правильными» отсечениями.
Свойства «правильного отсечения (Гомори)»:
линейные
отсекает найденные оптимальные нецелочисленные решения задачи (1)-(3)
не затрагивает ни одной из целочисленных точек задачи (1)-(4)
Необходимое условие применения метода Гомори – целочисленность всех коэффициентов и правых частей исходной задачи (в противном случае нарушается условие целочисленности дополнительных переменных).
В таблице найдено оптимальные, нецелочисленные решения ЗЛП (1) - (3) в котором
∈ Б
(базисные) переменные
Б
(небазисные)
Пусть
оптимальное решение
Б |
|
0 |
… |
0 |
… |
0 |
|
… |
|
… |
|
В |
|
… |
|
… |
|
|
… |
|
… |
|
|||
|
0 |
1 |
… |
0 |
… |
0 |
|
… |
|
… |
|
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
0 |
0 |
… |
1 |
… |
0 |
|
… |
|
… |
|
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
0 |
0 |
… |
0 |
… |
0 |
|
… |
|
… |
|
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
0 |
0 |
… |
0 |
… |
1 |
|
… |
|
… |
|
|
|
0 |
… |
0 |
… |
0 |
|
… |
|
… |
|
F(x) |
|
Ι. Полностью целочисленные задачи:
Алгоритм выбора наиболее эффективного отсечения.
Пусть и – нецелочисленные. Выбирают:
строку, соответствующую ∉ Z с наибольшей дробной частью:
если
=
,
выбирают строку, которой соответствует:
если
i
– порождающая строка.
|
У
коэффициентов ограничений и свободных
членов выделяют целую
|
и
дробную
части.
п
роизводящая
строка
+
+ … +
+…+
=
(1+
0)
+ ([
]
+
)
+ … + ([
]
+
)
+ … +([
]
+
)
= [
]
+
[ 0 +
+ … +
+ … +
]
+
=
-
(не
является допустимым решением)
ЗЦП
не имеет решения, если в симплекс-таблице
появляется, хотя бы одна строка с дробным
свободным членом (
)
и целыми коэффициентами
при переменных
(
)
(в этом случае соответствующие уравнение
не имеет решения в целых числах).
П
=
Б |
|
-3 |
8 |
6 |
0 |
0 |
0 |
В |
[ ] |
|
|
|
|
|
|
|
|
|
|||||||
|
8 |
-1/4 |
1 |
3/4 |
0 |
0 |
3/2 |
9/2 |
4 |
1/2 |
2 |
1/4 |
|
0 |
3/4 |
0 |
1/2 |
1 |
0 |
-1/2 |
7/2 |
3 |
1/2 |
7/4 |
2/7 |
|
0 |
-3/4 |
0 |
1/4 |
0 |
1 |
-1/4 |
4 |
4 |
0 |
- |
- |
|
1 |
0 |
0 |
0 |
0 |
12 |
36 |
- |
- |
- |
- |
|
поэтому
вычисляют
Строка, соответствующая – порождающая:
отсечение Гомори (для дальнейшего решения применяют двойственный симплекс – метод)
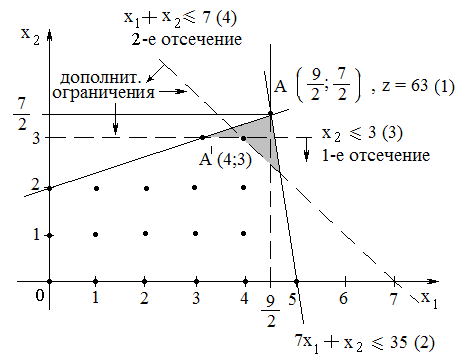
Пример 2:
|
|
Б |
|
7 |
9 |
0 |
0 |
В |
[ ] |
|
|
|
||||||||
|
|
|
|
|||||||||||||||
|
9 |
0 |
1 |
7/22 |
1/22 |
7/2 |
3 |
1/2 |
8/22 |
1 |
||||||||
|
7 |
1 |
0 |
-1/22 |
3/22 |
9/2 |
4 |
1/2 |
24/22 |
11/24 |
||||||||
|
0 |
0 |
28/11 |
15/11 |
6 3 |
- |
-
|
|
|
|||||||||
1/8
=
Б |
|
7 |
9 |
0 |
0 |
0 |
В |
Порождающая строка |
|||||
|
|
|
|
|
|||||||||
|
9 |
0 |
1 |
7/22 |
1/22 |
0 |
7/2 |
||||||
|
7 |
1 |
0 |
-1/22 |
3/22 |
0 |
9/2 |
||||||
|
0 |
0 |
0 |
-7/22 |
-1/22 |
1 |
-1/2 |
||||||
|
0 |
0 |
28/11 |
15/11 |
0 |
63 |
|||||||
|
9 |
0 |
1 |
0 |
0 |
1 |
3 |
- |
|||||
|
7 |
1 |
0 |
0 |
1/7 |
-1/7 |
32/7 |
|
|||||
|
0 |
0 |
0 |
1 |
1/7 |
-22/7 |
11/7 |
|
|||||
|
0 |
0 |
0 |
1 |
8 |
59 |
- |
||||||
Б |
|
7 |
9 |
0 |
0 |
0 |
0 |
В
|
|||||
|
|
|
|
|
|
||||||||
|
9 |
0 |
1 |
0 |
0 |
1 |
0 |
3 |
|||||
|
7 |
1 |
0 |
0 |
1/7 |
-1/7 |
0 |
32/7 |
|||||
|
0 |
0 |
0 |
1 |
1/7 |
-22/7 |
0 |
11/7 |
|||||
|
0 |
0 |
0 |
0 |
-1/7 |
-6/7 |
1 |
-4/7 |
|||||
|
0 |
0 |
0 |
1 |
8 |
0 |
59 |
||||||
|
9 |
0 |
1 |
0 |
0 |
1 |
0 |
3 |
|||||
|
7 |
1 |
0 |
0 |
0 |
-1 |
1 |
4 |
|||||
|
0 |
0 |
0 |
1 |
0 |
-4 |
1 |
1 |
|||||
|
0 |
0 |
0 |
0 |
1 |
6 |
-7 |
4 |
|||||
|
0 |
0 |
0 |
0 |
2 |
7 |
55 |
||||||
Общее
количество ограничений порождённой
задачи не должно превышать числа
переменных исходной задачи
.
В противном случае переменные,
ассоциированные с отсечениями Гомори
входят в базис, и соответствующие
равенства становятся избыточными (могут
быть исключены из таблицы).
Недостатки метода Гомори:
Ошибки округления, возникающие в процессе вычисления, приводят к получению нецелочисленного (неоптимального) решения.
Решения, последовательно получаемые в ходе реализации алгоритма, не являются допустимыми, т.е. алгоритм не позволяет получить целочисленных решений, не являющихся оптимальными (в случае остановки вычислений до момента окончания – целочисленное решение задачи не может быть получено).